混沌信号在抗干扰测量应用中的数字化处理

黄进燕,李嘉席

(1.西安电子科技大学,陕西西安710071;2.中国电子科技集团第五十四研究所,河北石家庄050081)

0 引言

混沌是非线性动力学系统特有的一种形式,是非线性系统中出现的类随机现象,其基本特征是对初始条件的敏感,加之在时域和频域具有可观的主旁瓣比以及较好的距离和速度分辨率,使得混沌信号具有极强的抗干扰性和极低的截获概率。混沌在电子工程中的应用研究领域已体现在测量、通信以及电子对抗等多个方面,特别是在电磁环境日趋复杂的背景下,混沌信号突出的抗干扰性能尤显重要。

混沌信号的产生主要有两类:一是由非线性电路直接产生功率谱合乎要求的超宽带混沌信号,比较典型的有以Colpitts电路为基础的一类电路和高维RC电路。另外一种就是由迭代或者数字方式产生较低频率的混沌信号,再由其调制产生特定频谱的超宽带信号。一般是以混沌调相或混沌调频的形式出现,在混沌雷达研究比较领先的国家,已经在研究一些实用性的基于混沌的雷达系统。本文针对抗干扰测量的应用背景,分析以Logistic映射为例的混沌信号的数字化处理和实现方案。

1 混沌信号在抗干扰测量系统中的应用

抗干扰测量系统由多路数字混沌信号产生器产生数字混沌信号经调相后进行变频、滤波功放等处理后由天线发射出去。接收部分将天线接收的回波信号经低噪混频后形成视频信号采样为数字信号后与多路数字混沌信号产生器产生的多路数字混沌信号进行相关处理,获取距离信息并进行多普勒估计从而得到速度信息。系统框图如图1所示。

通过控制多路数字混沌信号产生器产生不同延时间隔的数字信号,即可实现不同的距离分辨力。本文侧重讨论混沌信号的数字化处理。

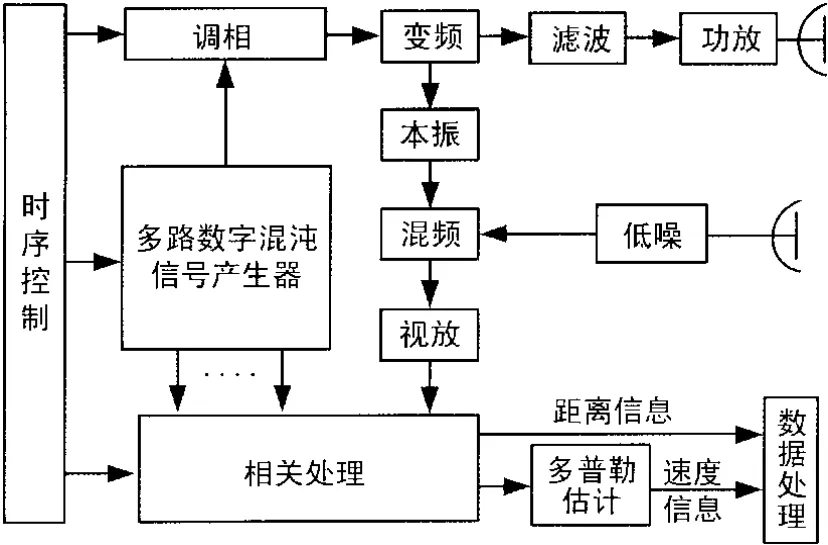
图1 抗干扰测量系统框图

2 Logistic映射

2.1 信号模型

Logistic映射具有多种形式,但各种形式间均可通过参数调整而相互转换。其中最具代表性的Logistic映射表达式为:

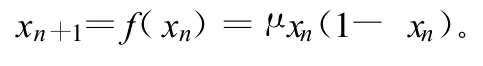
式中,μ∈(1,4];x∈(0,1)。

该式对应的是一个确定性可实现的非线性系统,可用于“预测”以xn为起点的下一个x值。研究结果表明,该动力学系统具有以下特点:

①系统输出状态取决于参数 μ,而同初始值x0无关。当μ∈(1,3]时,系统输出很快收敛于(0,1)间的某一常值,此时称作稳态,当 μ∈(3,4]时,稳定的不动点从吸引子变成排斥点,如图1(b)所示,即在μ=3处,稳定的周期一单线开始一分为二,大约在μ=3.449 6时周期二又分叉为周期四。随着 μ的增加,倍周期分叉越来越快,经n次分支,周期长度为2n,当 μ=μ∞≈3.571 448时,映射成混沌映射;

②在混沌映射时,系统具有初值敏感性、非周期等特性。所谓初值敏感性即在初始状态,2个相互很接近的值会随着时间的推移按指数分开;而非周期形是指此时输出信号时域表现出杂乱无章,频域表现出广谱性,相关函数近似为冲击函数,故又称似白噪声特性(或广谱特性)。

2.2 信号特性分析

为了获得最大的随机性,取μ=4。从而获得典型的Logistic映射:

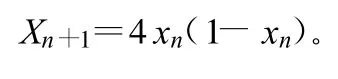
由此式仿真(取信号初始值x0=0.49)得到Logistic映射的信号波形、功率谱、自相关函数的仿真结果如图2所示。

图2 Logistic映射特性的MATLAB仿真结果

由仿真结果可知所选取的Logistic映射频谱平坦,其自相关峰值尖锐具有良好的自相关特性,从而有很好的抗干扰特性。

2.3 信号模糊函数分析

模糊函数(Ambiguity Function,AF)是波形设计与分析的工具,它可以方便地刻画波形与对应匹配滤波器的特征。AF在分析分辨率、副瓣性能以及多普勒和距离模糊方面非常有用,另外也可用于对距离-多普勒耦合的分析。

根据PM.woodward的定义[1],对于随机特性的信号应采用平均模糊函数形式。但对于实际信号处理的时限性,采用样本平均方式更现实一些。若信号处理时间为T,则混沌信号的平均模糊函数可以表示为:

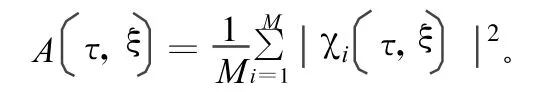
式中,i为第i个样本函数;τ和ξ分别为时间和频率,

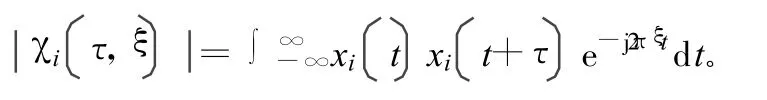
对离散时间信号有:

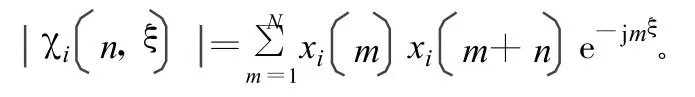
式中,m,n分别为时间变量和时间延迟。在计算中,可令所以上式可用DFT计算:

所以对应的模糊函数为:

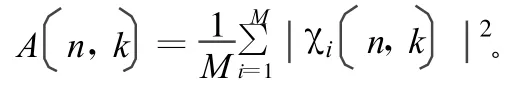
采用MATLAB进行仿真,取10个样本,每个样本100个点,仿真结果如图3所示。

图3 Logistic映射的模糊函数

由图3可以看到该混沌序列具有狭窄的中心峰值,即具有很高的距离和多普勒分辨率。较均匀的平坦区域说明具有低的且均匀的旁瓣从而使遮挡效应最小化。对于测量系统来说,这都是非常有益的。

由于在实际工程中所获得的不是理想的混沌信号,而是经过截断后的混沌序列。所谓截断的混沌信号实际上是对理想连续混沌信号的加窗处理。其模糊函数(时域加窗)[2]为:

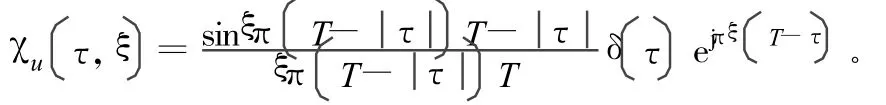
模糊图变成刀刃形,不过模糊面积在理论上为零,因此仍具有极佳的测距测速精度。

3 混沌信号的数字化处理

3.1 Logistic信号数字化

对于一般的混沌映射xn+1=f(xn),概率密度ρ(x)可由Perron-Froenious方程得到,即

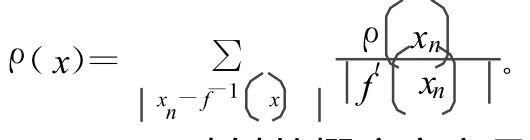
取μ=4,Logistic映射的概率密度函数为:

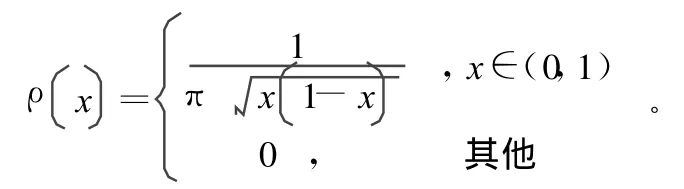
以初始值x0代入Logistic映射方程开始迭代,就可以得到混沌序列此时生成的混沌序列为实值序列,实际应用中需要对其进行数字化,得到二进制混沌序列。数字化方法有对称量化、门限量化、分布量化和比特抽取量化等,其中对称量化应用广泛。对称量化是将间隔I=[d,e]划分为d=t0＜t1＜…＜t2m=e,划分应满足下列条件为一组对称的门限,得到二进制函数为:

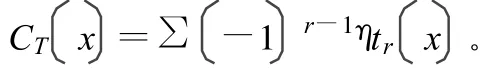
称为门限对称二进制函数。一般将该函数应用于不变侧度具有对称性的映射上,即满足:

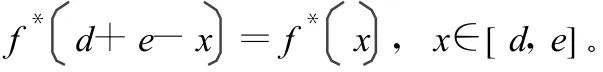
Logistic映射满足此条件,其均值为1/2,故以1/2为界,将它们数字化为-1和1,即得到数字混沌序列为:

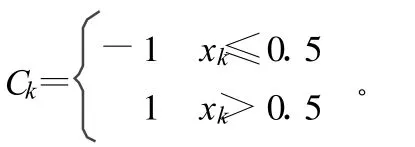
由平衡性知:数字化后序列均值为0,即¯C=0。

3.2 有限精度效应

由于混沌序列的遍历统计特性是建立在生成序列无限精度的基础上,然而实际的迭代运算并不能满足这个条件,只能在有限精度下进行迭代运算,这就产生了有限精度效应,即数字产生方法受有限字长的影响,就会使得所生成的混沌序列常常趋于周期性,或者是收敛于稳定解0。解决这一问题的有效方法可以在迭代的过程中分别对序列中的每个元素加入一个微小的扰动,从而破坏其周期性。目前降低混沌序列实现精度的方法主要有收缩法、m序列扰动法和正弦扰动法等。根据文献[3]的分析,正弦扰动法是最为简单且对精度要求不高。其表达式如下:

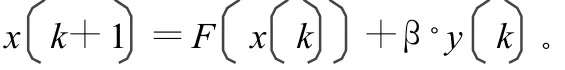
3.3 数字实现

采用ALTERA的FPGA实现Logistic信号的数字化。有限精度含义如下:如混沌映射的数值为01123456…,精度为1/100时,在处理时用100乘以0.123456…得到123.456…,取整后为123,在迭代计算的过程中,都用整数进行计算。同时,加入正弦扰动。其实现框图如图4所示。

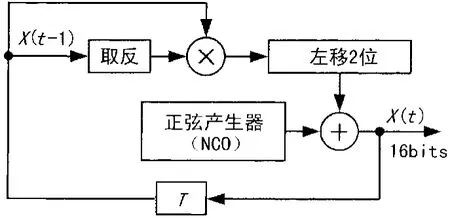
图4 Logistic序列FPGA实现框图

产生的序列数据经PCI总线由计算机获取并存储,对其频谱、自相关函数进行分析,分析结果表明产生的序列的统计特性良好,符合Logistic的混沌映射特性。

4 结束语

研究了以Logistic混沌信号为例的混沌信号数字化处理及实现,通过分析混沌信号的频谱、自相关特性和模糊函数,其强抗干扰性及较高的距离速度分辨力非常适用于抗干扰测量系统。

在FPGA中实现了Logistic混沌信号的在有限精度下的数字化处理,使得生成的序列具有较好的相关性能。采用该方法生成的混沌序列在抗干扰测量系统中有着较好的应用前景。

[1]WOODWARD PM.Probability and Information Theory with Application to Radar 2nd ed[M].New york:Pergam on Press,1964.

[2]谢红梅.基于混沌理论的信号处理方法研究[D].陕西:西北工业大学博士论文,2003:89-94.

[3]吴芝路,任广辉,赵 楠,等,混沌扩频序列有限精度研究[J].哈尔滨商业大学学报,2006,22(1):42-45.