晶体热膨胀的研究

尹会听，方正华

（安徽师范大学物理与电子信息学院，安徽芜湖 241000）

热膨胀是晶体最重要的基本性质之一。掌握晶体热膨胀的变化规律，对生产实践中合理选择和使用材料有着重要的意义[1]。

晶体温度上升体积膨胀，晶体平均原子间距在增加，原子的振动能量上升。严格来说，原子若作简谐振动，则振幅关于原子平衡位置对称，温度升高并不会使晶体体积膨胀。实际上原子的振动势能曲线并不是对称的抛物线，而是越向右越平滑，如图1中实线所示。

图1 原子振动势能曲线实线为非简谐振动势能曲线，虚线为简谐振动势能曲线.Fig.1 The curve of atomic vibration potential Solid lines for non-simple harmonic motion and dashed line for the simple harmonic motion.

水平直线与势能曲线的交点即为原子间距的最大值与最小值，其平均值可近似视为该温度下的原子平衡间距。实线描述了原子非简谐振动势能，随着温度的上升，其横坐标的平均值均大于r0，说明原子间平均距离加大，这正是热膨胀。

1 线膨胀系数的计算

原子在平衡位置r0时能量最低，原子由平衡位置向右偏离δ位移时，其势能为U（r0+δ）。将势能函数按泰勒级数展开如下[1]：

式中第一项为常数，即原子的最低势能，可取作零势能；第二项为零，表示原子处于平衡位置时只有动能；第四项为原子相互排斥的非谐项；第五项将反映晶体膨胀随温度的变化关系。

2 NaCl晶体的线膨胀系数β

以NaCl晶体为例，根据公式（7）计算不同温度下的线胀系数，所需参数见表1[3-4]。

实验中测得不同温度下NaCl晶体的体膨胀系数[5]，考虑到各向同性晶体体膨胀系数为线膨胀系数的3倍，可求出其线膨胀系数，见表2。

表1 线膨胀系数β计算参数Tab.1 Parameters for the linear expansion coefficient β calculation

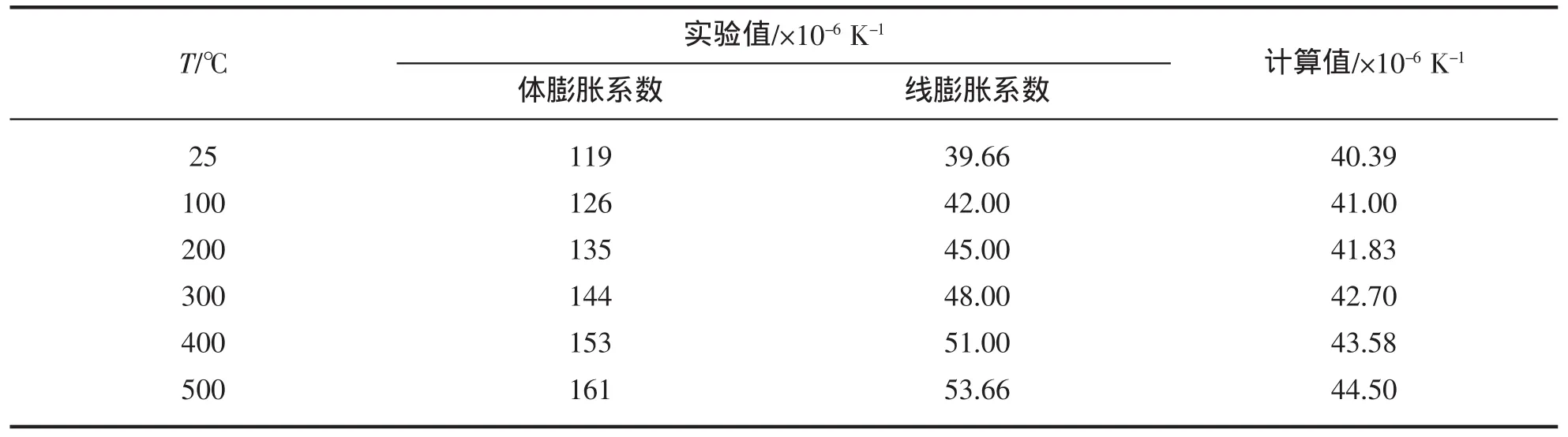
表2 膨胀系数——温度关系（P=0 kbar）Tab.2 The coefficient of expansion and temperature relationship（P=0 kbar）

从图2线膨胀系数β-T关系曲线可以看出理论计算结果与实验值在室温下符合较好，随着温度的升高偏差明显增大。

如果在推导线膨胀系数的计算公式时，势函数U（r0+β）的泰勒展开式中保留到更高级次项，则线膨胀系数的计算结果将会和实验值符合的更好；另外，短程势模型Morse势的表达式中参量α控制着势阱宽度，其值与固体物质体积弹性模量的一阶导数B＇有直接关系，存在α=B＇0-1。上面计算线膨胀系数过程中将α取作常数，而BOEHLER和KENNEDY发现B＇。随温度的增加并不稳定，且在200℃以上随温度的增加而逐渐减小，由此可得到表3[5]：

将在高温段缓慢减小的α值带入公式（7），计算出相应的线膨胀系数值，经修正后得到的线膨胀系数值见表4。

从图3线膨胀系数β-T关系曲线可以看出，经参量α修正后得到的理论计算结果与实验值在室温和高温下都符合较好。

图2 线胀系数β-T关系曲线Fig.2 The coefficient of linear expansion vs temperature

表3 参量α随温度变化值Tab.3 The value of parameter α following temper ature

表4 修正后膨胀系数——温度关系（P=0 kbar）Tab.4 The corrected coefficient of expansion and temperature relationship（P=0 kbar）

3 结果与分析

晶体温度升高，将具体物质的各相应参量代入由玻耳兹曼统计得到的原子平均位移公式，δ不为零，表明晶体中原子的振动主要表现为非谐振动，因而更合理地研究晶体的热膨胀，须考虑原子相互作用势的非谐项。在选用具体短程势模型Morse势计算NaCl晶体的线膨胀系数时，考虑到参量随温度的变化，计算的结果在室温和高温时和实验值都符合的较好，因此实践中可以用此法计算NaCl晶体或与其结构相同的晶体的线膨胀系数。

理论计算结果和实验值还存在的细微差别，主要考虑在理论推导时势函数按泰勒级数展开后应保留比δ更高的级次以更好反映非谐振动对晶体膨胀的贡献；还可以考虑选用更好的短程势模型来替换Morse势进行计算。另外，实验必然存在误差，因此也期待会有更好的热膨胀系数实验值出现。

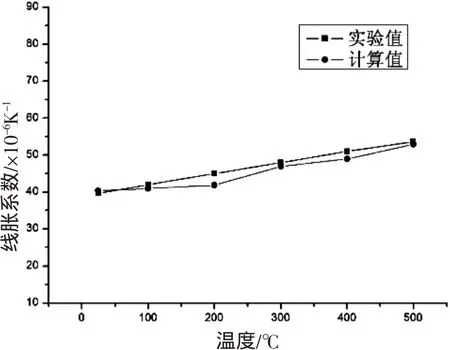
图3 修正后线胀系数β-T关系曲线Fig.3 The corrected coefficient of linearexpansion vs temperature

[1]郑国桢,林苗华,林德明.金属材料热膨胀系数经验公式的探讨[J].广东工业大学学报,1999,16(3):1-8.

[2]RUFFA A R.Thermal expansion and melting in cubic crystals[J].Physical Review B,1981,24(12):6 915-6 925.

[3]RUFFA A R.Statistical thermodynamics of insulators[J].J Chem Phys,1985,83(12):6 405-6 412.

[4]RUFFA A R.Thermal expansion in insulating materials[J].Journal of Materials Science,1980,15:2 258-2 267.

[5]BIRCH F.Equation of state thermodynamic parameters of nacl to 300 kbar in the high-temperature domin[J].Journal of Geophysical Research,1986,91:4 949-4 954.