基于轮廓模板匹配的物体检测算法

陈 雷

同济大学软件学院，上海 201804

基于轮廓模板匹配的物体检测算法

陈 雷

同济大学软件学院，上海 201804

本文提出了一种基于轮廓模板匹配技术的物体识别检测算法。物体检测器使用部分已有的轮廓图片，通过AdaBoost训练得出。此算法达到了一般基于纹理检测器的效果，而且更加简单且易于实现。

轮廓模板 ；Chamfer；Boost

1 概述

我们的模型训练方法采用了一种过饱和的模式，即使用冗余的特征集合进行训练，而这些冗余特征集合恰恰克服了同类物体的不同点（如不同的体型、不同的动作以及不同的面部表情）、图像场景变化（不同的光照条件、遮挡等）。

2 检测

整个检测器是建立在局部的基于轮廓特征匹配基础上的，匹配算法使用了方向性的Chamfer距离考量，这个距离值通过其权重求和，并最终作为物体检测分类器。特征集合F代表了物体的轮廓T的局部片段，每个特征都包括了它自身到物体中心的偏移量p。另外的3个参数分别是：方向量的权重λ，检测阈值θ以及特征权重量a。

2.1 方向性Chamfer匹配

Chamfer匹配技术在轮廓匹配应用中非常广泛。它提供了一种计算两个轮廓距离量的方法，并且在有大量非对齐的情况下，仍有很高的鲁棒性。从最简单的模型讲，Chamfer匹配需要两个边缘点集，图像边缘点集E={e}和匹配模板点集T={t}，下面的公式描述了计算这两个点集在偏移量为x情况下的Chamfer值：

NT为T中点的数量。这个公式计算了匹配模板中的边缘点到最近的图像边缘点的平均距离。通过预处理，例如距离变换（Distance Transform），计算Chamfer距离的效率会提高很多，公式（1）即可以转化为公式（3）：

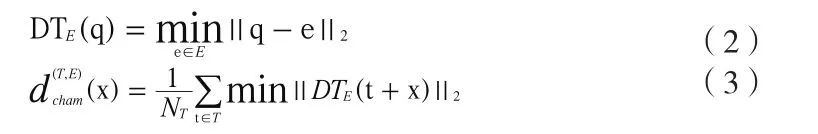
欧几里得距离DT的计算可以参照文章[1]。

另外，一个很大的改进，就是引用了轮廓的方向考量。这种考量通过边缘点的斜率来表达。在图像点集中，通常有很多地方边缘非常嘈杂混乱，方向性Chamfer距离可以很好的解决这个问题。其中一种技术是将图像和匹配模板中的边缘点划分为不同的几个离散的方向通道，并求出Chamfer值的和。但这种方法的通道数量并不明确，而且需要格外注意连个通道之间的边缘曲线。我们使用一种略微不同的方法，精确的计算匹配模板上每个边缘点斜率与图像中每个边缘点斜率的差：

o(·)代表一个边缘点的斜率，|o1-o2|表示计算两个点的斜率差，ADTE(t+x)表示在点集E中找出离点(t+x)最近的一个点。

这样，最终的方向性Chamfer值便可以通过下面的公式计算出来了：

其中，λ为方向考量的权重值。

2.2 检测步骤

物体检测器K(c)可以计算某一点的c的信心值（Confident Value），使用K在整个图片的所有像素点进行扫描，可以得出一个分类图。这个分类图经过一定的处理（如降噪、平滑等），通过设定一个理想的阈值，在这个分类图中可以找出物体在图片中的大致位置。

整个检测器K通过一个参数组{Fm}进行训练，每个参数组表示为Fm=（Tm ,pm ,λm ,θm ,am），K用加性模型表示如下：

δ函数相当于一个判断语句，如果括号内部表达式为真，则返回1，否则返回0。θm是每个一个阈值，来过滤弱分类器得出的方向性Chamfer值，通过训练得出。am是每个特征向量的权重，同样通过训练得出。

3 训练

3.1 建立匹配模板库

首先，我们要找出大量需要检测的物体图片，将其分成两部分，第一部分则用来提取特征，第二部分则用来用来作为训练样本。首先将第一部分的图片背景信息去除（通常是下载标准数据集来解决），然后使用Canny edge算法算出这些图片相应的边缘轮廓图片。随机指定一些位置，记录这些位置到物体中心的偏移量，并截取随机大小的矩形区域的（不能太大或太小）轮廓片段，将这两种信息储存。这样，库中的每条信息都包括两个内容：物体的部分轮廓曲线以及它相对于物体中心的位置。

3.2 分类器的学习

Boost是现今机器学习领域中较为简单且有效的技术。它由一系列的“弱分类器”构成，这些分类器的表现仅仅比随机猜测要好一点，但是一个带有权重的弱分类器的集合，通常可以构成一个比较准确的“强分类器”。Boost算法在计算机视觉中的应用非常广泛，大部分是作为一个特征选择机制，例如：Viola和Jones利用AdaBoost制作了一个效率很高的级联分类器。

我们引入Boost算法主要是为了3点：特征选择，参数估计以及检测器学习。

4 实验分析

我们使用Caltech人脸数据集进行算法的测试验证。如图1，左边一列都是包含检测物体的图片，中间是通过训练好的检测器算出的分类图，右边列则是检测器K中匹配模板叠加后的效果。可以看出，需要检测的物体的位置都比较准确。

图1

5 结论

本篇文章对基于轮廓模板匹配的物体检测技术进行了探讨，并且使其达到了一般基于纹理检测算法的效果。但是此算法所检测的都是某一确定大小的物体，而通常图片中的物体大小都不是固定的。如何解决这个问题，则是我们今后要研究的。

[1]P.F.Felzenszwalb and D.P.Huttenlocher.Distance transforms of sampled functions. Technical report,Cornell, 2004.

[2]J.Friedman, T.Hastie, and R.Tibshirani.Additive logistic regression∶ a statistical view of boosting.Annals of Statistics, 2000, 38(2)∶337-374.

TP391

A

1674-6708（2010）30-0158-02