现有桥梁剩余寿命预测方法研究
陈 默
兰州交通大学土木工程学院(730070)
我国自20世纪80年代起桥梁工程的工作重点逐步转移到养护维修、鉴定评估和加固改造方面。因此,合理评估与预测现有混凝土桥梁的承载能力与剩余寿命,具有重要的安全、技术与经济意义。
1 结构使用寿命预测的一般方法
使用寿命与材料性能、细部构造、暴露状态、劣化机理等许多因素及其相互作用有关而难以量化,目前对结构使用寿命的预测通常只能考虑其中的一个主要因素,主要方法有:
1)基于经验的预测方法:根据试验室和现场大量试验结果与经验积累,对使用寿命作半定量预测,包含了经验知识和推理。
2)基于类比的预测方法:假定混凝土在某一期限内是耐久的,则相似环境下的相似混凝土也将有同样的寿命。
3)基于加速试验的预测方法:混凝上结构的耐久性试验多采用加速试验,依据试验后的损伤程度,对使用寿命进行预测,应用范围有限制。
4)基于数学理论模型的预测方法:对所评估的结构研究得比较透彻,通过建立计算寿命的模型,并结合测试数据进行计算,推断其剩余寿命的办法。
5)其他方法:基于力学理论模型的预测方法、基于概率分析的预测方法、基于灰色理论的预测方法等。
2 基于可靠性理论的桥梁结构剩余使用寿命预测
可靠度方法建立在可靠度—时间关系的基础上,认为结构可靠度衰减到可接受的最小值或者失效概率增大到可接受的最大值的时间为使用寿命。对结构进行评估,并准确的预测其剩余使用寿命具有重要的工程意义。文献[1]提出了已知β反求时间t的思路,并结合文献[3]所述的可靠性评定标准,引入目标可靠指标βm,最终实现了结构剩余使用寿命的预测。对现存结构寿命预测的可靠度分析应考虑结构已承受过荷载作用而并没有破坏这一特点。现存结构在将来某段时间内的失效概率是某一使用荷载a(验证荷载)发生后的条件概率。在实际工程中,很难获得某一具体结构的验证荷载。所以可以通过考虑结构已使用年限内安全工作的条件概率来预测。
设结构的寿命为X,其分布函数为F(X),则结构的寿命大于x的概率可以表示为:
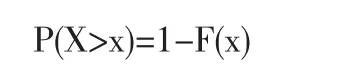
结构在X内的失效概率为 Pf(x)=F(x)=Φ(-βx),其中βx为结构在:x内的可靠指标,随着x的变化而变化,是一个动态可靠指标。
若该结构己经运行了t0,则它的剩余寿命Y可以表示为:
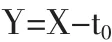
结构的剩余寿命Y大于某一个T的概率应该为一条件概率,即
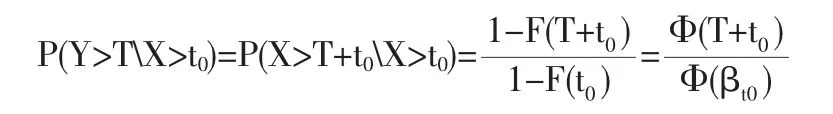
相应的失效概率为:
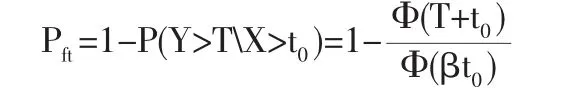
由此可得结构在剩余使用寿命期T内的可靠指标为:
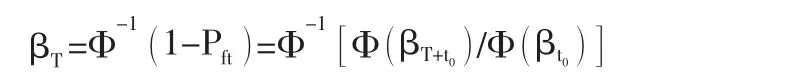
结合文献[1]所述,按照结构安全性等级划分的标准,至少应满足 b级,相应的可靠指标为βb=2.7,即βT≥βb。
由此,可以推导出:
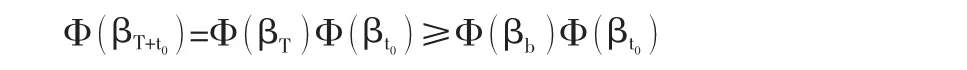
式中Φ(ΒT+t0)可按文献[3]所讲方法计算,所以上式是T+t0的函数,可以求解,所以结构剩余寿命可预测。
3 结束语
1)在已有研究成果的基础上,简单介绍了结构使用寿命预测的一般方法和基于可靠性理论的桥梁结构剩余使用寿命预测得方法。2)在役桥梁达到剩余使用寿命终点也并不意味着桥梁的完全失效,而是不宜再继续承载,需要对主要承重构件进行加固。
[1]穆加宇.结构可靠性理论在桥梁工程中的应用.
[2]邹挑花.结构可靠性理论在桥梁状态评估和寿命预测中的应用[J].科学论坛,2008,1(下):21-22.
[3]徐礼军.现役桥梁结构动态可靠度应用研究.
[4]刘斌云,霍达.现有混凝土桥梁结构剩余寿命预测方法研究[J].市政·交通·水利工程设计(2008)02-0078-04:78-80.

