Multisim软件在含受控源线性电路教学中的应用

孙 韬，侯世英，周 静，彭文雄

（重庆大学 电气工程学院，重庆400044）

受控源是伴随电子器件和部件，尤其是半导体技术的发展而引入的一种理想二端口电路元件。如果一个线性电路不含有受控源，则根据KCL、KVL和电路元件的伏安关系可建立线性独立的电路方程，各支路电压电流的解存在而且唯一；当线性电路中引入受控源后，其电路方程可能不具有线性独立性，从而导致电路解的性质发生变化［1－2］。由于难以用实际元器件构成理想的线性受控源，加上实际元件的精度难以保证，参数的调试也不方便，因此采用Multisim仿真软件对含受控源线性电路进行仿真分析不仅可以弥补实验条件的不足，还可以加深学生对电路理论基础知识的进一步理解。

1 Multisim仿真软件简介

Multisim软件是EWB的升级版本。EWB是加拿大IIT公司于20世纪80年代末、90年代初推出的基于Spice的电路设计与仿真虚拟电子工作台软件。从EWB6.0版本开始，IIT公司对EWB进行了较大规模的改动，并将仿真设计模块更名为Multisim。它集成了电路图编辑，高性能模拟、数字电路及混合电路的仿真功能，具有丰富的元件库，具有使用方便的虚拟仪器仪表库。

Multisim最重要的特点是：仿真手段切合实际，元件和仪器仪表与实际情况非常接近。元件、仪器仪表选取方便，并可扩充；仪器的操作如图使用真实仪器，容易学习。另外，在Multisim仿真软件中可以对电路设置故障，以观察故障情况下电路的各种状态，使学生加深对各种原理的理解，这在实际实验是难以做到的。

Multisim软件拥有完备的分析手段，提供了直流工作点分析、交流分析、瞬态分析、傅里叶分析、噪声分析、失真分析、参数扫描分析、温度扫描分析、极点一零点分析、传输函数分析、灵敏度分析、最坏情况分析和蒙特卡罗分析、批处理分析、用户定义分析、噪声图形分析和射频分析等，可以极大地方便设计人员对电路性能进行分析［3－4］。

Multisim软件的突出优点是将电路图输入、SPICE仿真器、元器件库、仪表库集成并融合在一起，相当于一个设备先进、功能完备的大型电子实验室。同时，实验的过程可以搬上多媒体屏幕，与理论课程的教学融为一体。

2 软件在电阻电路教学中的应用

受控源兼有两个基本性质：一是电源性质；二是电阻性质。因为受控源的输出量电压或电流依赖于控制量，只要控制量存在，则输出端就有电压和电流，即向外电路提供能量，故受控源具有电源的作用和性质。受控源的四种类型的性能方程也表明：表征受控源输出特性的数学方程是以电压或电流为变量的代数方程，根据受控元件的定义，受控源也可作为电阻元件。

正是由于受控源基本性质的复杂性，以及各种含有受控源电路模型的多样性，目前还没有一种通用的简便的分析方法，使得含有受控源电路的分析方法具有多样性和复杂性。在有关线性电路的分析方法的文献中已经提及到，当一个网络中不含受控电源时，其节点电导矩阵Gn、割集电导矩阵GQ和回路电阻矩阵R1都为对称矩阵，很任意通过观察法直接列写出网络方程的矩阵形式。当网络中含有受控电源时，这些矩阵一般情况都不是对称矩阵，那么这给列写方程和计算都增添了难度，传统的教学方法使得学生在理解这部分内容时存在一定的困难。

为了简化分析过程和得出相关的结论，文中所分析的含受控源线性电路应具备以下的两条性质：

（1）所有的电阻都是线性正电阻，电路中不存在纯电压源回路和纯电流源割集；

（2）所有受控源的控制量和被控量不在同一支路，否则受控源就有可能表现为纯电阻的性质。

例1在图1所示的受控源电路中，电阻的参数为G1＝2S，G2＝2S，G3＝4S，G4＝5S，G5＝2S，G6＝5S，电源的参数为Us1＝2V，Is3＝2A，Is6＝5A，以节点2的电压作为受控源的控制量，由观察法所得的节点电压方程的矩阵形式为

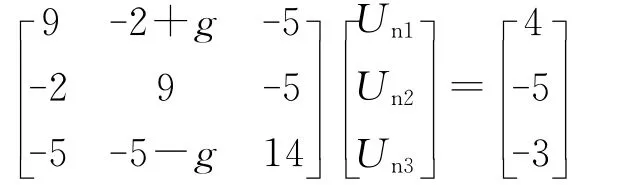
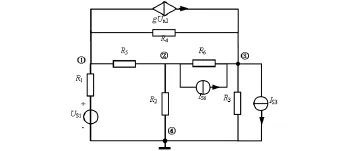
图1 含受控源的线性电阻电路

该方程系数矩阵的行列式值为528－2g，因此，当受控源的参数g＝264S时，电路是无解的，否则该电路的解是唯一。图2所示为Multisim仿真电路，这里以节点1、2、3的电压电压作为输出变量，对受控源的参数在260S至268S之间进行线性扫描分析（Parameter Sweep），扫描的步长为2S，参数扫描的分析结果如表1所示，可以看出，由于仿真软件采用数值计算的原因，当受控源的参数g＝264S时，节点的电压高达109～1012V数量级，相当于此时电路是无解的，而当受控源的参数取其它数值时，电路的解是存在并且是唯一的。

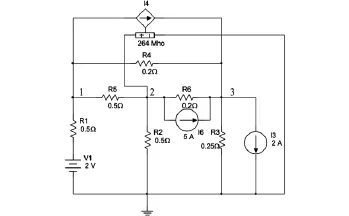
图2 含受控源线性电阻电路的Multisim仿真1

在图1所示的电路中，如果将G3由4S改为5S，那么此时该电路的节点电压方程的矩阵形式为

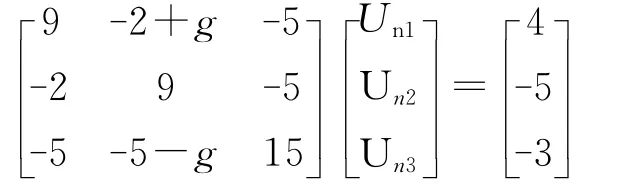
该方程系数矩阵的行列式值为605，与受控源参数无关，也就是说，不管受控源参数如何取值，该电路的解始终是唯一。其受控源参数的扫描分析结果如表2所示，可以看出，在扫描区间内，电路的解总是存在并且是唯一的。

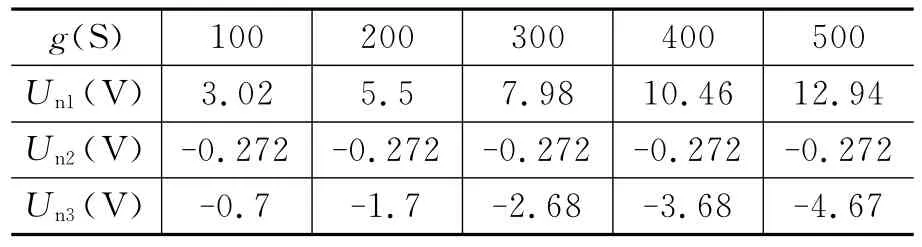
表2 受控源参数对节点电压的扫描计算结果2

例2在图1所示的电路中，假设G3、G4和G6都为0，其余元件参数不变。那么对各个节点分别列写KCL方程可以求出各个支路的电流，但是此时的问题却在于，当计算节点1的电压时，由电阻R1和R5计算所得的结果肯定是矛盾的，并且节点3的电压也不能确定，因此，在该电路中不管受控源的参数如何选取，电路是无解的。图3所示为Multisim仿真电路，受控源参数的扫描分析结果如表3所示，可以看出，受控源的参数在扫描区间内，节点3的电压是不存在的，因此电路是无解的。

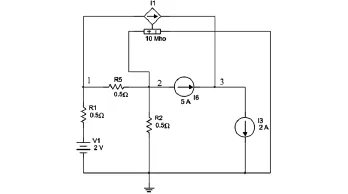
图3 含受控源线性电阻电路的Multisim仿真2

表3 受控源参数对节点电压的扫描计算结果3

在对含受控源线性电阻电路的仿真表明，如果受控电流源与纯电流源支路构成割集的情形下，不管受控源的参数取什么数值，电路是无解的；根据对偶原则，如果受控电压源与纯电压源支路构成回路，不管受控源的参数取什么数值，电路也总是无解的；在其余的情形下，在受控源参数的变化过程中，电路最多出现一种无解或有无穷多个解的情况。

3 Multisim在二阶电路教学中的应用

含受控源的线性动态电路只考虑二阶电路，因为对一阶电路而言，一般都可以通过戴维南等效电路消除受控源，其解的性质就如同不含受控源的一阶线性电路。对于图4所示的线性二阶电路，包含了一个VCCS，其控制量为电阻两端的电压。

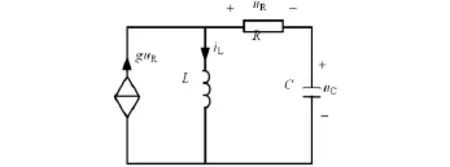
图4 含受控源的线性二阶电路

所得关于电容电压uC（t）的微分方程为

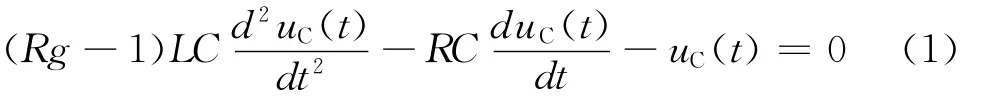
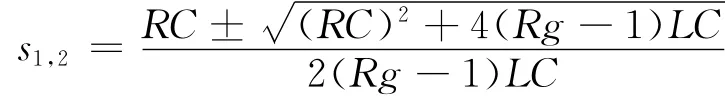
由上式可知，当受控源参数发生变化，有可能使特征根出现正的实部，那么将会使系统变得不稳定。

例3在图4所示的电路中，假设元件的参数为R＝1Ω，L＝1mH，C＝1μF，初始条件为uC（0＋）＝5V，iL（0＋）＝0A，其 Multisim仿真电路如图5所示为，以电容电压作为输出变量，对受控源的参数分别取值0.2、0.5、1、1.5、2进行扫描分析，参数扫描的分析结果如图6所示，可以看出，当受控源的参数g＝1时，该电路相当于一阶电路，暂态过程很快就结束；当g＞1时将使电路变得不稳定。

在对含受控源线性二阶电路的仿真表明，电路的解始终是存在的，只不过当受控源的参数发生变化时，二阶电路可能会等效为一个一阶电路。

从方程（1）可以看出，当受控源参数g＝1／R时，方程为一阶微分方程，电路相当于RC一阶电路；当受控源参数g≠1／R时，特征方程的特征根为

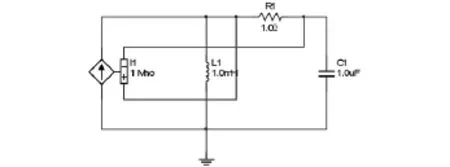
图5 含受控源线性二阶电路的Multisim仿真

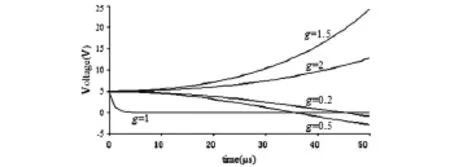
图6 线性二阶电路的Multisim仿真曲线

4 结语

在电路理论教学中融入Multisim仿真，使理论教学与仿真验证相结合，将抽象的理论知识变成直观的感性认识；同时，应用仿真软件进行教学，可以弥补一些实验条件的不足，有效克服传统实验的局限性，有利于解决由于硬件条件限制不能开出和因课时限制没有时间开出的实验项目，让学生有机会完成更多的实验。

［1］ 蔡少棠，葛守仁.线性与非线性电路［M］.世界图书出版公司.1992

［2］ 江泽佳.电路原理（上、下）［M］.人民教育出版社.1979

［3］ 付志红主编.计算机辅助电路分析［M］.高等教育出版社.2007

［4］ 王延才.基于Multisim的电路仿真分析与设计［J］.计算机工程与设计.2004，25（4）：654－656