电子邮件系统中PGP的改进研究

郑玉丽 刘翠香

洛阳理工学院 河南 471023

0 引言

随着计算机网络的广泛普及，电子邮件运用的日趋频繁，几乎所有上网的人每天都要收或发电子邮件，特别是商业邮件，对安全性的要求更高，但是人们对它的安全性似乎没有随着时间推移而增强。虽然电子邮件系统提供了极好私密性PGP保障安全，但是随着黑客技术的更新，邮件的私密性越来越显得不安全。因此，现行使用的基于大整数分解的RSA公钥算法，以及DES对称加密算法的PGP，已经明显滞后而且在方案设计上也亟待改进。鉴于此，针对现行PGP，本文采用能够快速加解密的椭圆曲线公钥密码体制 ECC和高级对称加密算法AES有机结合，特别又增加了时间戳DTS技术，提出了电子邮件安全管理的新方案。本方案进一步增强电子邮件的安全性，同时也解决了目前PGP中速度和安全性不能兼顾的问题。

1 算法设计

1.1 公钥对称加密算法选择

椭圆曲线指的是由韦尔斯特拉斯 Weierstrass方程y2+a1xy+a3y=x3+a2x2+a4x+a6所确定的平面曲线 E，此外再加上一个叫做无穷远点的特殊点O。

在ECC中，采用了定义在有限域上的椭圆曲线，其方程为y2=x3+ax+b(mod n) ，其中4a3+27b2(mod n)≠0，x、y、a、b ∈Fn，这里n是素数，a和b为两个小于n的非负整数。由满足此方程的点(x,y)和一个无穷远点O就组成了椭圆曲线E。

椭圆曲线离散对数问题 ECDLP定义如下：给定素数 n和椭圆曲线E，对Q=kP，在已知P，Q的情况下求出小于n的正整数k。可以证明，已知k和P计算Q比较容易，而由Q和P计算k则比较困难，至今没有有效的方法来解决这个问题，这就是椭圆曲线加密算法原理之所在。

数字签名算法基本过程(假如A方签名，B方验证)如下：

（1）A方先确定合适的椭圆曲线E，确定基点G、大素数n，选取私钥d∈[1，n-1]，计算Q=dP，生成公钥(E,P,n,Q)并公布；并对消息生成摘要e；

（2）签名

① 选择一个伪随机数k∈(1，n-1]，计算kP=(x1,y1)；

② 计算r= x1mod n，若r=0，回到第①步；

③ 计算s= k-1(e+dr)mod n，若s=0回到第①步；

④ 生成签名(r,s)，并发送签名和消息m；

（3）验证

① B方收到签名(r,s)和m，对m生成摘要e；

② 计算(x1,y1)= s-1eP+ s-1rQ(mod n)，如果x1=r，则验证成功。

公钥加密基本过程(假如B方给A方发送信息m)如下：

（1）A方先确定合适的椭圆曲线E，基点G，大素数n，私钥k，再生成K=kG，生成公钥(E,P,n,Q)并公布。

（2）B方把消息m嵌入椭圆曲线上一点M；

（3）用A方公钥加密：选取一个伪随机数r∈(1,n-1]，计算C1=M+rK,C2=rG；把C1、C2发给接收方B；

（4）A收到 C1、C2后，用自己的私钥进行解密M=C1-kC2，恢复出明文M；

（5）再把明文M解码恢复出原有信息m。

1.2 安全散列函数(SHA-2)

本方案对电子邮件信息产生摘要选用SHA-2(SHA-224、SHA-256、SHA-238、SHA-512)算法。它是比SHA-1更长更安全的散列算法。它也是目前美国国家标准和技术研究所(NIST)公布的最安全的散列算法。

1.3 AES算法

2000年，NIST经过三轮候选算法筛选，从众多的分组密码中选出Rijndael算法作为高级加密标准(AES)。

Rijndael算法的特点如下：采用SP结构、加密、解密相似但不对称、支持128/32数据块大小、支持128/192/256密钥长度、有较好的数学理论做为基础、结构简单、速度快等。AES的加密算法的数据处理单位是字节，128位的比特信息被分为16个字节，按顺序复制到一个4×4的矩阵中，称为状态(state)，AES的所有变换都是基于状态矩阵的变换。在轮函数的每一轮迭代中，包括四个变换，分别是字节代换运算(ByteSub())、行变换(ShiftRows())、列混合(MixColunms())以及轮密钥的添加变换(AddRoundKey())，其作用就是通过重复简单的非线性变换、混合函数变换、将字节代换运算产生的非线性扩散，达到充分的混合，在每轮迭代中引入不同的密钥从而实现加密的有效性。

1.4 数字时间戳

日期和时间是E-mail中的重要内容之一，需要加以确认与保护。数字时间戳(Digital Time Stamp,DTS)服务较好地解决了E-mail发送时间的安全问题。

时间戳是一个经加密后形成的凭证文档，它包括三个部分：需加时间戳的文件的摘要；DTS收到文件的日期和时间；DTS 的数字签名。时间戳产生的过程为：用户首先将需要加时间戳的文件用 Hash 编码加密形成摘要，然后将该摘要发送到 DTS，DTS 在加入了收到文件摘要的日期和时间信息后再对该文件加密，然后送回用户。

2 PGP方案设计

假设用户A使用PGP向用户B发送电子邮件E-mail，发送方用户A向用户B发送电子邮件的流程如图1，步骤如下：

第一步：发送方A

（1）对E-mail信息M使用散列函数SHA-2生成摘要；

（2）把上一步生成的摘要和自己的身份信息发给数字时间戳机构DTS，申请E-mail数字时间戳DTS(M)，并保存；

（3）生成对称密钥K，对DTS(M)和e-mail信息M进行加密，生成密文EK(M)和EK(DTS(M))；

（4）对EK(DTS(M))使用发送方A的私钥进行签名，生成签名SA(EK(DTS(M)))；

（5）对生成的签名用接收方B的公钥再次进行加密，生成密文EB(SA(EK(DTS(M))))；

（6）把 EK(M)和 EB(SA(EK(DTS(M))))发给 Internet，通过Internet传给接收方B。

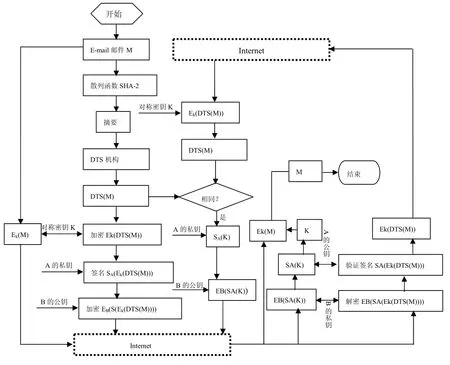
图1 改进的PGP方案

第二步：接收方B

（1）从 Internet上接受发送方 A 发过来的 EK(M)和EB(SA(EK(DTS(M))))；

（2）使用B的私钥解密得SA(EK(DTS(M)))；

（3）使用A的公钥解密得EK(DTS(M))；

（4）把EK(DTS(M))发到Internet上，传给发送方A。

第三步：发送方A

（1）接受到B传来的EK(DTS(M))；

（2）使用对称密钥 K进行解密得 DTS(M)，记为 DTS‘(M)；

（3）比较解密得来的DTS‘(M)和A在第一步中自己保存的DTS(M)；

（4）如果DTS(M)和DTS‘(M)相同，则对对称密钥K，使用A的私钥加密，生成SA(K)，再使用接收方B的公钥加密，生成密文EB(SA(K))，并发到Internet，通过Internet传给接收方B；否则结束对称密钥K的发送。

第四步：接收方B

（1）从Internet接收到EB(SA(K))，用自己的私钥进行解密，得SA(K)；

（2）使用发送方的公钥解密得对称密钥K；

（3）使用对称密钥K对第二步收到的EK(M)进行解密，得到M，即发送方发来的E-mail明文。

3 方案分析

本文主要从方案设计上分析，新增加了时间戳技术，对时间戳进行了3次加密发给接收方，接收方B收到后进行2次解密，把解密后的时间戳密文回发给发送方A，发送方对其进行比较验证，从而预防了重放攻击。

本方案从算法的选择上分析，非对称加密算法选用了ECC，这种算法与现行使用的RSA相比，可以用较少的密钥长度获取更高更大的安全强度；对称加密算法选用SHA-2，进一步增强了破解难度。

从计算开销上分析，对 E-mail信息使用对称加密，对E-mail的时间戳和对称密钥K使用了非对称加密算法的混合加密方案，本方案收发双方共进行了5次加密和6次解密，加密次数减少一次，并且对E-mail信息只使用对称密钥加密，没有再进行非对称加密算法加密。这些措施，在安全性增强的同时，很大程度地减少了计算开销，降低了加解密的时间，提高了加解密的速度。

4 结束语

本文提出的PGP新方案，不仅从算法选择上增强了传统的PGP的机密性，身份认证可靠性，数据完整性，不可抵赖性，而且加入了时间戳技术，从而抵御了重放攻击，另外还降低了计算开销，加快了加解密速度。从而在增强安全的同时兼顾了加解密速度。

[1]段保护,王建.数字签名技术的新探讨[J].计算机工程与科学.2009.

[2]Wongoo Lee,Jeakwang,Lee. Design and implementation of secure e-mail system using elliptic curve crptosystem[J]. Future Generation Computer Systems.2004.

[3]Woei-Jiunn Tsaur , Chih-Ho Chou. Efficient algorithms for speeding up the computations of elliptic curve cryptosystems[J].Applied Mathematics and Computation 168.2005.

[4]赖顺天.PGP 工作原理及其安全性[J].计算机安全.2008.

[5]冯登国.网络安全原理与技术[M].北京:科学出版社.2003.