带牵顶伞的大面积环帆伞充气性能分析

尚小娟 童明波 张红英

(南京航空航天大学 航空宇航学院,南京210016)

1 引言

随着航天技术的发展,载人飞船技术也日益兴起,对其回收系统也提出更高的要求。

在航天回收中,环帆伞因具有许多优点而被广泛应用。但是由于载人飞船回收系统采用的降落伞面积大,开伞程序复杂,容易受到伞衣尾流、高空突风等干扰气流的影响[1]。因此,在高速开伞过程中,伞衣之间容易出现了摩擦抽打,致使伞衣出现局部强度损失,在后续的充气过程中进一步遭到破坏,而伞衣的局部破损对载人航天回收构成严重的安全威胁,因此必须采取控制主伞开伞状态的措施,本文着重研究,在主伞顶部增加一具牵顶伞,以控制主伞开伞状态,降低主伞开伞动载,防止伞衣之间的摩擦抽打[2],并分析充气过程中牵顶伞对主伞充气形状等的影响,得出牵顶伞的充气性能,以便后续的工程应用。

2 降落伞充气过程的数值模拟

降落伞的充气过程是一个复杂的非线性、时变过程,涉及到流体力学和结构力学中几个复杂的现象,包括透气性、非流线型物体的气体动力学、大变形柔性结构的动力学问题、气动弹性力学、物-伞系统快速减速引起的时变流动现象等,理论分析十分困难[3]。充气过程决定于伞衣底边区域的伞衣幅形状、伞衣品质以及伞衣的透气性参数。

降落伞模型的简化假设:1)整个主充气过程中伞绳部分具有零弯曲刚度,即不发生“绳帆”现象;2)伞的质量集中于伞衣底边中心,伞衣充气过程中,伞的质心相对底边的位置保持不变;3)由于是轴对称伞,在对伞衣质点进行相应处理后,可在伞衣对称面内进行二维流场计算;4)假设伞绳、加强带和伞衣是弹性体,符合虎克定律。[4]

充气过程的简化假设:1)对称充气;2)假定伞衣已全长拉直并开始进入充气阶段;3)开伞过程中伞顶始终保持球冠形状;4)考虑伞衣透气量和伞顶孔的影响。

2.1 伞衣结构动力学模型

降落伞是一个复杂的气动弹性体,具有敞开式织物可拉伸透气结构。一般把降落伞当成是由具有连续性、较小相对厚度和较大变形量的薄膜材料组成。由此,可将降落伞离散为一系列用阻尼弹簧连接的质点,采用质点阻尼弹簧模型来描述伞衣的结构受力。

2.2 计算流体力学模型

降落伞伞衣的厚度很小,远小于伞衣的几何尺度。因此从流体力学的角度来考虑,可以把伞衣看成是薄膜材料,其厚度对流场本质不会产生影响。在对降落伞进行流体力学数值模拟时可以忽略伞衣厚度的影响。由于所关心的是伞衣张开时交界面的压力差,对附面层干扰及涡系结构只作大致了解。考虑到雷诺平均Navier-Stokes方程所需的计算网格数量小,耗费的计算资源及计算时间都较少,因此,选用雷诺平均NS方程数值求解程序,使用LU-SGS隐式推进方法及ROE的通量差分分裂格式,并结合带非线性限量因子的MUSCL插值方法[5]。

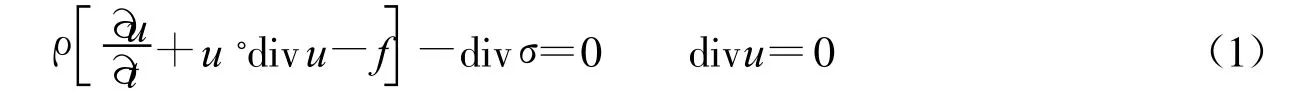
式中 ρ为大气密度;u为速度;t为时间;σ为主应力;f为体积力。

为了尽可能缩小远场边界条件对研究对象周围流动的影响,选择长为10R(R为降落伞投影半径),宽为6R的矩形作为计算域,并采用矩形网格进行填充。其中沿气流纵向前边界为4R,后边界为6R。整个计算域被分成多个子区域,各个子区域相互对接构成流场空间。为了适应粘性计算与捕捉分离涡的需要,采用了网格局部加密。

计算中边界条件的设定情况为:降落伞表面为无滑移壁面边界,对称面为对称边界条件,计算域的其它面均定义为压力远场,选择理想气体模型[6]。

2.3 计算流体力学-结构动力学(CFD-MSD)耦合模型

采用松散耦合,即将上个时间步长流体方程的计算结果传给结构方程并进行下个时间步计算,由结构计算得到新的结果,然后再传给流体方程进行新的一轮计算。程序结构图如图1所示。

这种耦合方式的计算速度大大提高,但是有可能使计算不稳定。耦合方法运用准定场假设进行分析,即认为每一个时间点处流场是定常的:先根据初始数据,在每一时间步长开始时,降落伞到达一个新位置,将伞面附近的流场网格点移动至伞面上;通过修改这些点相应的动量方程,更新源项,利用CFD程序计算得出交界处质点的压差系数,将计算结果传给结构动力学(MSD)方程,进行表面力计算和进行伞面变形运动计算,得到下一形状,依据下一形状,流场计算程序进入下一个时间步长,开始新一轮的计算。

图1 程序结构图

3 仿真结果与分析

3.1 主伞充气过程外形变化

通过仿真计算得到了环帆伞充气过程伞衣外形变化、伞衣周围流场变化、伞衣阻力特征变化和开伞动载等的变化。在充气阶段,空气首先在伞衣顶部聚集,使伞衣顶部膨胀,然后膨胀部分向伞衣底边扩展,直到伞衣完全张满。

将计算仿真结果(如图2)与试验拍摄图片(如图3)进行对比,发现吻合较好,说明所建立的数学模型可以用于降落伞充气过程的数值仿真计算。

图2 带牵顶伞的主伞充气过程伞衣外形变化

图3 充气过程伞衣外形变化实验拍摄图

3.2 牵顶伞阻力系数分析

(1)牵顶伞阻力系数随充气时间的变化

初始充气阶段定义为伞衣充气开始至伞顶孔即将被冲开这一时间段受主伞尾流的影响,牵顶伞所受阻力(即载荷)与自由来流条件不同。为了便于研究该阶段牵顶伞阻力的变化规律,定义初始充气过程的特征时间为:

式中 t0为初始充气开始时间;tn为初始充气结束时间;t为当前时刻。

牵顶伞阻力系数Cd为:

式中 D为牵顶伞受到的阻力;ρ为大气密度;V为降落伞下降速度;S为牵顶伞迎风面积。

计算所得的牵顶伞在初始充气阶段的阻力系数Cd随的变化规律如图4(a)所示,在初始充气的前半段,Cd保持在0.8左右,之后则大致呈线性规律下降。为了工程应用的简便,可以设定Cd在初始充气的前半段保持为常数,在后半段采用线性公式拟合。图4(a)显示了以=0.4作为分界点的拟合结果,得到的Cd表达式为:

图4 牵顶伞阻力系数随时间的变化

考虑到牵顶伞在解除收口绳之前即失效,只分析主充气阶段开始至收口绳张紧这一时间段内牵顶伞阻力系数的变化。计算所得的牵顶伞阻力系数随时间的变化如图4(b)所示。

在主充气阶段初期,随着伞顶孔的冲开,牵顶伞阻力系数大致呈线性上升,之后则下降至0.4左右,总的来看其规律性不如初始充气阶段明显。考虑到伞顶孔冲开过程相对整个主充气过程并不长,为了工程上的简便,可以使用0.4作为主充气阶段开始至牵顶伞失效这一时间段内的牵顶伞阻力系数。

(2)牵顶伞阻力系数随连接带长度的变化

牵顶伞位于降落伞轴线上,阻力系数与其前方来流动压成正比,因此通过分析轴线上动压的变化,可以预测不同连接绳长度下牵顶伞的阻力系数变化情况。设轴线上动压为Q,牵顶伞与主伞顶部距离为L,图5(a)显示了=0.75时计算所得的Q随L的变化规律。

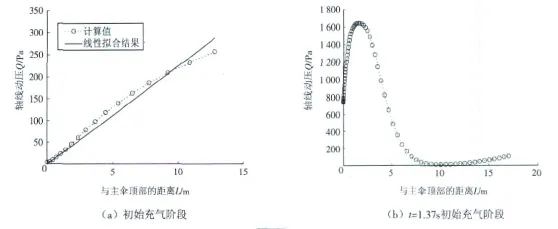
图5 轴线动压Q随牵顶伞与主伞顶部距离L的变化

在图中L的取值范围(0m≤L≤13 m)内,Q与L呈近似线性关系,可以拟合得到一条斜率为22.5过原点的直线。又由于阻力系数Cd与动压Q成正比,因此有:

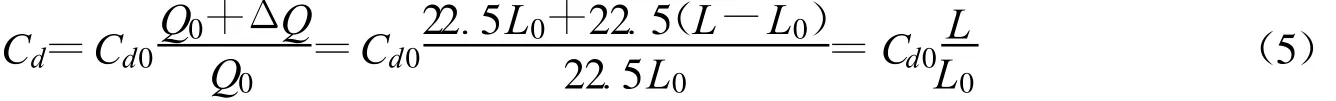
式中 ΔQ为动压变化量;Q0为原始大气压;L0为当前设计的牵顶伞与主伞顶部的距离;Cd0为当前设计的牵顶伞阻力系数。

结合式(4)和式(5)有:

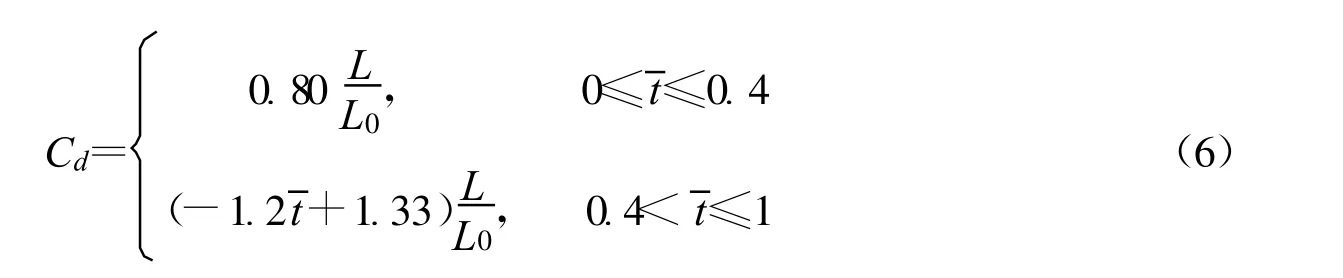
主充气阶段,轴线动压Q随牵顶伞与主伞顶部距离L的变化如图5(b)所示。可见,主充气阶段Q与L的关系比初始充气阶段复杂,不利于使用简单的公式表达。另外,由于主充气阶段主伞尾涡对流场有显著影响,不同充气时刻的流场变化较初始充气阶段大,因此这里不再试图以公式的形式表达牵顶伞阻力系数随连接绳长度的变化关系。

(3)牵顶伞阻力系数随投影面积大小的变化

在均匀的自由来流中,牵顶伞增大或减小,其阻力系数将基本保持为常数。但牵顶伞处于主伞的尾流之中,来流速度不等于主伞前的来流速度(降落伞的下降速度),且来流速度分布不均匀,见图6,因此其阻力系数将随着牵顶伞直径(或面积)的变化而变化。

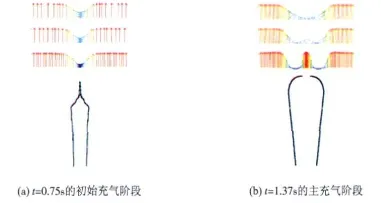
图6 主伞尾流的速度矢量

计算所得的初始充气阶段牵顶伞阻力系数随迎风面积的变化,如图7(a)所示。牵顶伞位于距离伞顶孔较近的区域,其阻力系数Cd随迎风面积S的变化规律如图7(b)所示。Cd随S的增大而减小,这与初始充气阶段的变化规律相反。两者之间的线性关系不如初始充气阶段明显,不同时刻斜率的差别也比初始充气阶段大,不利于得出Cd与S之间的简单表达式。但与初始充气阶段类似,Cd随S的变化并不剧烈,因此如果牵顶伞大小变化不大,可以使用当前设计的阻力系数作为近似值。

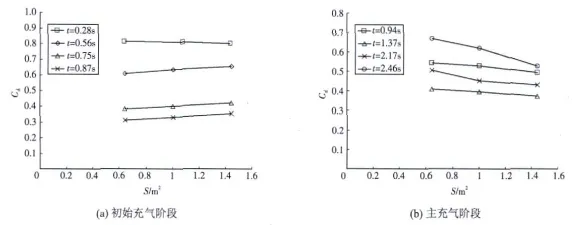
图7 牵顶伞阻力系数与其迎风面积的关系

可见,牵顶伞阻力系数与迎风面积大致呈线性关系,且在不同时刻的斜率基本一致,约为0.05。因此,牵顶伞阻力系数与其迎风面积的关系可以表示为:

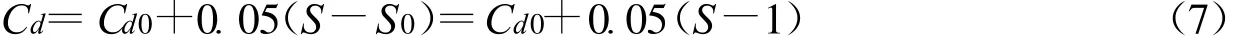
式中 S0和Cd0分别为当前设计的牵顶伞迎风面积和阻力系数,S0=1.003≈1.00,Cd0可以根据式(6)计算得到。结合式(6)和式(7)即可得到不同面积的牵顶伞在初始充气阶段各个时刻的阻力系数公式:

需要指出的是,以上公式只在牵顶伞在宽度方向上完全处于主伞尾流内时有效。从图7(a)可以看出,主伞尾流宽度与主伞已冲开的直径相当,因此,当牵顶伞直径大于主伞已冲开直径时,以上公式不再适用。

图6(b)显示了t=1.37s时主伞尾流的速度矢量。受伞顶孔射流的影响,在距离伞顶孔较近的区域,降落伞轴线上主伞尾流速度高,往外速度降低,然后再增大至来流速度。在距离伞顶孔较远的区域,伞顶孔射流的影响减弱,呈现中心速度低,外侧速度高的特点,与初始充气阶段的主伞尾流速度分布类似。

4 结束语

采用流固耦合的计算方法对带牵顶伞的主伞充气过程进行了数值模拟,通过计算得到了主伞充气过程外形变化情况,并与试验结果进行了对比;对牵顶伞阻力系数的变化进行了分析,给出了适合工程估算的牵顶伞阻力系数公式。

[1]Sundberg W D.Status Report:Parachute System Design,Analysis and Simulation Tool[R].AIAA 93-1208,1993.

[2]林斌.牵顶伞设计分析[C].中国宇航学会返回与再入专业委员会学术会议论文集.南宁:中国宇航学会返回与再入专业委员会,2006:74-78.

[3]潘星,胡利,曹义华.降落伞主充气阶段的动态仿真及流场分析[J].航空动力学报,2008,23(1):87-93.

[4]余莉,史献林,明晓.降落伞充气过程的数值模拟[J].航空学报,2007,28(1):52-57.

[5]张红英,秦福德,刘卫华,等.牵顶伞对主伞充气过程的影响[J].南京航空航天大学学报,2010,42(1):47-51.

[6]彭勇,张青斌,秦子增.降落伞主充气阶段数值模拟[J].国防科技大学学报,2004,26(2):13-16.

[7]滕海山.航天器回收降落伞系统设计程序介绍[J].航天返回与遥感,2005,26(1):24-27.

[8]苏媛,邓辉.降落伞物理模型和充气过程的系统仿真分析[J].系统仿真学报,2003,15(4):560-563.

[9]彭勇,程文科,宋旭民,等.降落伞充气过程研究方法综述[J].中国空间科学技术,2004(3):38-44.

[10]张青斌,王显,宋旭民,等.降落伞载荷分析介绍[J].航天返回与遥感,2003,24(4):1-4.