海水环境下混凝土的断裂能及其应变软化

张 鹏,孙志伟,赵铁军,W ittmann F H ,2

(1.青岛理工大学耐久性与可持续发展研究中心,山东青岛266033;2.Aedificat Institute Freiburg,Freiburg,Germany)

海水环境下的钢筋混凝土结构,如海港码头、海洋平台、跨海大桥和隧道等,由于海水侵蚀,结构过早破坏的现象非常严重。对于这些严酷环境下的钢筋混凝土结构,其耐久性已引起广泛关注。对于海水中所含的Cl-、SO42-、M g2+等有害离子对混凝土耐久性造成的耐久性破坏以及相应的防护措施,已进行了大量试验研究和工程实践[1-3];然而,除了上述化学腐蚀外,海水还能够对混凝土的强度和断裂能等造成一定的影响,但从这一角度来研究海水等盐溶液对混凝土的劣化作用却往往被忽视,相关文献尚不多见。Cook等人[4]曾就水和甲醇浸泡对砂浆和混凝土强度和长度的影响变化进行了试验研究,M atsushita和Onoue[5]也从液体表面张力的角度就多种液体对水泥砂浆静态抗压强度和疲劳强度的影响进行了试验研究,但都没有涉及海水等盐溶液对混凝土断裂能的影响。断裂能也是混凝土材料耐久性的一个重要指标,研究海水对混凝土断裂能及其应变软化的影响,有助于深入理解和重视海水对混凝土材料产生的严重劣化作用,进而对海水环境下的混凝土结构采取相应的防护措施。

该文采用带初始切口梁的三点弯曲试验和楔形劈拉试验2种方法,对完全干燥、半干燥、水浸泡、海水浸泡以及不同浓度NaCl盐溶液浸泡状态下的混凝土试件进行了试验研究,测定了不同含水状态时混凝土的荷载-位移曲线,计算了各种混凝土的断裂能值,并通过Consoft软件进行逆向分析得到了不同状态下混凝土的应变软化曲线,研究了海水对混凝土断裂能及其应变软化的影响。

1 混凝土断裂能与应变软化

G riffith[6]在研究玻璃等脆性材料时首先提出了断裂理论,并根据经典力学和热力学能量平衡原理引入了应力和材料表面能的关系,如式(1)所示。

式中,σ表示材料所受拉应力;γ表示材料的表面能,即产生单位面积所需要的能量;E为材料的弹性模量;c为材料在应力作用下产生的裂缝宽度的一半;μ为泊松比。

对于理想的脆性材料,Griffith公式能够有效地描述在单轴拉力作用下裂缝的形成和材料的失效过程,但对于多孔的非均质混凝土材料,由于其断裂过程消耗的能量取决于固体物质的表面能和每个单位断裂的粒子数,这意味着在没有水分和其它液体进入混凝土孔隙的情况下,只有断裂的固体粒子表面能对能量平衡有贡献。但当混凝土孔隙中存在一定含量的水分或其它液体时,其表面能则必须需考虑液体表面张力的影响,由式(2)进行计算[5]。

同时,大量研究也认为[7-9],混凝土并非完全脆性材料,当混凝土达到临界应力时,在其宏观裂缝的端部会产生一个类似金属材料塑性区的断裂过程区,并按应变软化曲线来传递应力;只有当应变达到混凝土的软化极限时,混凝土才完全断裂。混凝土断裂能即定义为产生单位面积的裂缝所需要的能量,是混凝土材料单元粒子表面能的宏观反映,表征混凝土的断裂性能。

理论上来说,混凝土的应变软化曲线是高阶非线性的,其数值计算一般较难实现。因此,针对广泛采用的三点弯曲试验和楔形劈拉试验,通常采用简化的软化曲线来进行分析计算,如线性[10]、双线性[11-12]和三线性[13]模型等。该文采用Consoft软件[11]对混凝土试件的荷载-位移曲线进行了逆向分析,按双线性模型模拟了混凝土的应变软化行为,同时也计算了混凝土的断裂能值,研究讨论了海水对混凝土断裂韧性的影响作用。由于直接拉伸试验很难实现,不适合作为混凝土断裂能测试的标准方法,该文采用了国际材料与结构实验室联合会(RILEM)混凝土断裂力学委员会建议的带切口梁三点弯曲试验[14]和楔形劈拉试验[15]方法。

2 试验

2.1 原材料与试件制备

试验原材料包括：P.O 32.5级青岛山水水泥;5～20 mm连续级配的花岗岩质碎石,密度为2 620 kg/m3,压碎指标为5.8%;青岛大沽河砂,细度模数为2.7,中砂,密度为 2 610 kg/m3;自来水;萘系高效减水剂。混凝土试件的水灰比为0.5,配合比如表1所示。

表1 试验用混凝土的配合比/(kg◦m-3)

试验用混凝土试件包括：用于三点弯曲试验的100 mm×100 mm ×515mm棱柱体,用于楔形劈拉试验的200mm×200 mm×40 mm试件。试件成型24 h后拆模,放入标准养护室(20±3℃,RH ＞90%)中养护至28 d龄期,随后取出试件按三点弯曲试验(2.2)和楔形劈拉试验(2.3)的要求将试件加工成型。然后将所有试件放入105℃的烘箱中烘干14 d直至完全干燥,取出试件待降至室温后将所有试件分为6组,每组6个试块,3块用于三点弯曲试验,另3块用于楔形劈拉试验。6组试件包括：第1组为完全干燥试件;第2组试件放入相对湿度为75%的室内环境6周,使混凝土与环境湿度达到一致而部分含水;第3组试件浸泡于水中14 d;第4组浸泡于青岛地区的海水(其中NaCl的浓度为3.1%)中 14 d;另2组分别浸泡于浓度为 5%和23.4%的NaC l盐溶液中14 d。上述处理完成后,对这6种不同含水状态下的混凝土试件进行三点弯曲试验和楔形劈拉试验,每种情况取3个试块的平均值。

2.2 三点弯曲试验

该文三点弯曲试验采用了RILEM推荐的带切口梁三点弯曲测定混凝土断裂能的试验标准[14]。所用试件尺寸为100 mm ×100 mm ×515mm,如图1所示,2个支点跨距为500 mm,试件中心处用切割机制作初始切口,缝高比a/h为0.5。

在万能试验机上进行,2个引伸计固定在试件侧面用来测定跨中初始缺口处的位移(挠度)变化,荷载传感精度为0.1 N,位移传感精度为 0.001 mm。加载采用恒定位移速率0.3 mm/min,由计算机同步记录试件的荷载-位移曲线。混凝土试件的断裂能G f(N/m)可根据公式(3)进行计算。

式中,M为荷载-位移曲线与坐标轴所围成的面积;W为试件沿长度方向的线密度;δ0为试件最终破坏时的挠度变形;A lig为试件的断裂韧带面积。

2.3 楔形劈拉试验

楔形劈拉试验也采用了RILEM推荐的试验方法[15]。试件尺寸为200 mm ×200 mm ×40 mm,在进行劈拉试验前,在试件上表面的中心处制作一个凹槽和一个缝高比为0.5的初始裂缝,如图2所示。加载也采用恒定位移速率0.3 mm/min,由计算机同步记录试件的荷载-CMOD(Crack M outh Opening Disp lacement裂缝张开位移)曲线。

图2 楔形劈拉试件示意图

根据式(4)计算混凝土试件的断裂能值(N/m),式中符号M和代表的意义与式(3)相同。

3 结果分析与讨论

3.1 不同含水状态下混凝土的荷载-变形曲线和断裂能值

对6种不同含水状态下的混凝土进行三点弯曲试验和楔形劈拉试验后得到荷载-位移曲线,通过Consoft软件逆向分析拟合后的结果如图3和图4所示。可以看出,无论是三点弯曲试验还是楔形劈拉试验,结果都显示,混凝土在完全干燥时所能承受的荷载最大;而当混凝土处于相对湿度75%环境和浸于水中时,水泥基体吸收水分,在内部孔隙中形成水膜,当水膜越厚时,根据多孔材料表面能的表述式(2)可以认为混凝土的表面能变小,而根据公式(1)又可以得到材料所承受荷载能力与表面能之间的关系,如式(5)所示,即相对临界荷载的平方等于相对表面能。

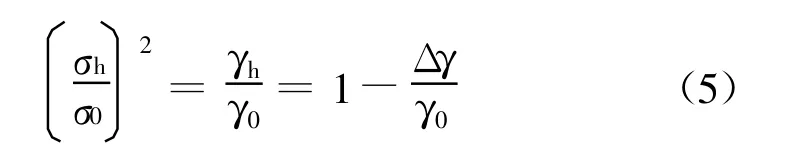
式中,σh为含一定水分时混凝土的临界荷载,σ0为完全干燥混凝土的临界荷载,γh为一定含水状态时混凝土的表面能,γ0为干燥混凝土的表面能,Δγ为其表面能损失。这说明,混凝土孔隙中的水分越多,其表面能就越低,进而造成混凝土的荷载承受能力随之下降,正如图3和图4中完全干燥、75%RH和水浸泡3种状态混凝土的荷载-位移曲线所示。

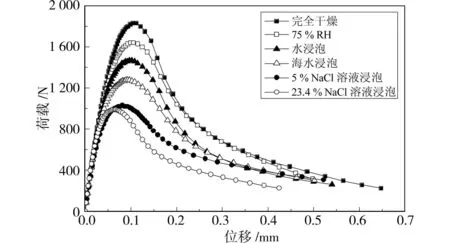
图3 不同含水状态下混凝土三点弯曲试验的荷载-位移曲线

图4 不同含水状态下混凝土楔形劈拉试验的荷载-位移曲线

根据式(3)和式(4)分别对图3和图4所示三点弯曲和楔形劈拉试验得到的数据进行计算,得到6种不同状态下混凝土的断裂能值,如表2所示。由结果可见,混凝土在完全干燥时具有的断裂能最大,但当混凝土吸收水、海水和高浓度盐溶液后,断裂能依次下降。究其原因,是由水、海水、高浓度NaCl溶液的表面张力不断增大引起的。根据式(2),当混凝土完全干燥即液体表面张力为0时,方程左侧即混凝土断裂表面能具有最高值;一旦水分进入混凝土孔隙中,本试验所用水的表面张力为72.1 m N/m,根据式(2)则断裂能势必变小;而当海水和高浓度NaCl溶液侵入混凝土时,由于试验所用青岛地区海水的表面张力为73.5mN/m,配制的5%NaCl溶液的表面张力为74.2 mN/m,23.4%NaCl溶液的表面张力则为85.5 m N/m,由式(2)可推断,随着进入试件开放孔隙中溶液的表面张力不断增大,混凝土的断裂能随之下降,试验结果也完全表明了这一趋势。

并且,经过海水和NaCl溶液浸泡后的混凝土试块在三点弯曲和楔形劈拉试验中所承受的最大荷载也较水浸泡时更低,水浸泡后混凝土的最大承载力较完全干燥时降低了19.6%(三点弯曲试验)和14.5%(楔形劈拉试验),而海水浸泡后则降低更多,分别为28.9%和21.7%。这一现象出现的原因同样归结为溶液表面张力的增大引起断裂能下降,当试件承受荷载时,积存于试件中的应变能达到一定极限后以断裂表面能的形式释放形成裂缝,因此,海水和NaCl溶液浸泡后混凝土断裂能下降的情况下,根据式(5),承载力也随之下降。

另外,2种试验方法得到的断裂能值并不完全相同,这主要是由于三点弯曲试验和楔形劈拉试验时混凝土试件的受力方式以及裂缝扩展方式不同造成的,前者为受弯破坏,初始裂缝出现在试件底部,而后者为受拉破坏,裂缝由试件上部扩展;并且,三点弯曲试验还受到支座摩擦和支座局部屈服的影响,以及试件自重在试验过程中消耗能量等,由其得到的断裂能值稍小。2种试验方法所测结果的轻微差别并不影响本试验结论。

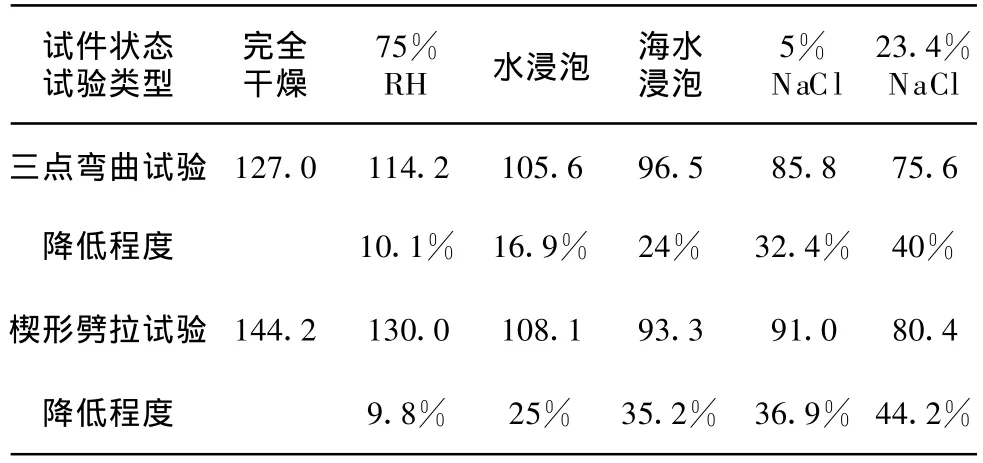
表2 不同状态下混凝土的断裂能及其降低程度/(N◦m-1)

由图3和图4还发现,经过海水和NaCl溶液浸泡后的混凝土,在三点弯曲和楔形劈拉试验中所承受的最大荷载比水浸泡时更低。水浸泡后混凝土的最大承载力较完全干燥时降低了19.6%(三点弯曲试验)和14.5%(楔形劈拉试验),而海水浸泡后则降低更多,分别为28.9%和21.7%。这是由于海水和NaCl盐溶液的表面张力比水高引起的,21℃左右时,测定试验中所用水的表面张力为72.1 mN/m,青岛地区海水的表面张力为 73.5 mN/m,配制的5%NaCl溶液的表面张力为 74.2 mN/m,23.4%NaCl溶液的表面张力则为85.5 mN/m,由此,根据式(2)和式(5),混凝土的承载力势必随着液体表面张力的增大而不断下降。当水、海水以及NaCl溶液进入混凝土内部孔隙后,混凝土的表面能下降,这意味着形成新的面积所需要的能量减少,整个混凝土试件宏观初始裂缝的扩展所需要的外力功就越少,表现为混凝土加载点变形能力变差,断裂能降低。根据式(3)和式(4)分别对三点弯曲和楔形劈拉试验得到的数据进行计算,得到6种不同状态下混凝土的断裂能值,如表2所示。可见,混凝土在完全干燥时具有的断裂能最大,但当混凝土吸收水、海水和盐溶液后,断裂能依次下降。另外,2种试验方法得到的断裂能值并不完全相同,这主要是由于三点弯曲试验和楔形劈拉试验时混凝土的受力方式以及裂缝扩展方式不同造成的,前者为受弯破坏,初始裂缝出现在试件底部,而后者为受拉破坏,裂缝由试件上部扩展;并且,由于三点弯曲试验还受到支座摩擦和支座局部屈服的影响,以及试件自重在试验过程中消耗能量等,由其得到的断裂能值稍小。

3.2 不同含水状态下混凝土的应变软化曲线

需要指出的是,2种材料的断裂能相同时,其应变软化曲线并不一定完全相同,因此,在判断混凝土材料的断裂韧性时,需要同时评价其断裂能和应变软化性能。通过Consoft软件对6种不同含水状态的混凝土试件的荷载-位移曲线进行了逆向分析,按双线性模型模拟了混凝土的应变软化行为,6种不同状态混凝土的三点弯曲和楔形劈拉试验的双线性应变软化曲线分别如图5和图6所示。由结果明显可见可以看出,完全干燥时混凝土的抗拉强度最高,软化阶段也呈现较好的韧性,但随着水、海水和高浓度盐溶液进入混凝土内部孔隙,使得孔溶液表面张力增大,引起混凝土表面能下降,这意味着材料内压发生变化,固体粒子的平均拆开压力增大,砂浆与骨料的咬合力以及骨料间的互锁能力减弱,骨料对裂缝的延迟机制不明显,混凝土形成新的裂缝面积所需要的能量就越少,整个混凝土试件宏观初始裂缝的扩展所需要的外力功也就越少,并且开裂后的裂缝发展更不稳定,混凝土表面能下降,水泥浆体和骨料之间的咬合力也变弱,表现为混凝土加载点变形能力和韧性变差,抗拉强度相应下降,降低,变形能力和韧性也随之变差,裂缝更易形成和扩展。

图5 不同含水状态下混凝土三点弯曲试验的应变软化曲线

图6 不同含水状态下混凝土楔形劈拉试验的应变软化曲线

因此,对处于海水和除冰盐环境下的混凝土结构来说,除了氯离子等有害介质的侵入能够引起钢筋锈蚀和耐久性失效外,水以及含有NaCl的海水和盐溶液还能够造成混凝土承载力、断裂能和断裂韧性减弱,因此,在对海水环境下的混凝土结构进行耐久性设计和施工时,还需考虑海水对混凝土的这些影响作用并采取相应措施。对此,W ittmann等人[16-17]提出对混凝土表面进行硅烷浸渍防水处理,一方面可以有效抑制海水和氯离子侵入混凝土内部孔隙,减小孔隙内水分含量;另一方面,硅烷分子能够在混凝土孔隙壁上形成一层憎水膜,改变水与固体的接触角,由未处理时的锐角转变为钝角,根据多孔材料表面能表达式(2),从而相应提高混凝土的表面能及其断裂韧性;但鉴于海水环境的极端恶劣性,对于该处理方法的长期有效性,还有待于进一步系统研究。

4 结 论

1)随着混凝土内部孔隙中水和海水的进入,混凝土表面能降低,造成材料荷载承受能力显著下降,水浸泡后混凝土承载力较完全干燥时降低了19.6%(三点弯曲试验)和14.5%(楔形劈拉试验),海水浸泡后则降低更多,分别为28.9%和21.7%。

2)混凝土完全干燥时具有最高断裂能,但当水、海水和高浓度盐NaCl溶液侵入混凝土后,由于液体表面张力的增大导致混凝土断裂能和断裂韧性大幅下降;海水浸泡状态下混凝土的断裂能较干燥时降低了24%(三点弯曲)和35.2%(楔形劈拉)。

3)海水浸泡后,混凝土的承载力、断裂能和软化韧性均减弱,裂缝更容易形成和扩展,这对于海水环境下的混凝土结构设计和施工来说,应当引起足够重视。

[1]赵铁军.混凝土渗透性[M].北京：科学出版社,2006：1-6.

[2]GJØRV O E.Durability design o f concrete structures in severe environment[M].1st ed.Oxon：Taylor&Francis,2009.

[3]GEH LEN C.Durability design according to the new model code for service life design [C] ∥TOUTLEMONDE K,SAKA I K and GJØRV O E.Fifth International Conference on Concrete Under Severe Conditions：Environment and Loading.Paris,France：Laboratoire central des ponts et chausses,2007：35-50.

[4]COOK D J,HAQUE M N.Strength reduction and length changes in concrete and mortar on w ater and methano l sorp tion[J].Cement and Concrete Research,1974,4(5)：735-744.

[5]M ATSUSHITA H,ONOUE K.Influence of surface energy on comp ressive strength o f concrete under static and dynamic loading[J].Journal of Advanced Concrete Techno logy,2006,4(3)：409-42.

[6]GRIFFITH A A.The phenomena of rup ture and flow in solid[J].Philosophical T ransactions of the Royal Society of London,1921,A 221：163-198.

[7]V ILLMANN B,VILLMANN T,SLOWIK V.Determ ination of softening curves by backw ard analyses of experiments and optim ization using an evo lutionary algorithm[C]∥LIV C,LEUNG C K Y,W ILLAM K J,et al.Proceedings of Fram cos-5 Fracture Mechanics of Concrete Structures,Vail Cascade Resort,Vail Colorado,USA：Tay lor&Francis,2004：439-445.

[8]ØSTERGAARD L,OLESEN JF.Comparative study of fracturemechanical test methods for concrete[C]∥LI V C,LEUNG C K Y,WILLAM K J,et a l.Proceedings o f Fram cos-5 Fracture Mechanics of Concrete Structures, Vail Cascade Resort, Vail Colorado,USA：Tay lor&Francis,2004：455-462.

[9]FERRETTI E.A discussion of strain softening in concrete[J].International Journal of Fracture,2004,126(n1)：L3-L10.

[10]H ILLERBORG A.Results of three comparative test series for determ ining the fracture energy of concrete[J].Materials and Structures,1985,18(107)：407-413.

[11]SLOWIK V,V ILLMANN B,BRETSCHNEIDER N,et al.Com putational aspec ts o f inverse analyses for determ ining softening curves of concrete[J].Computer M ethods in Applied M echanics and Engineering,2006,195(52)：7223-7236.

[12]W ITTMANN F H,SUN Z W,ZHAO T J.Strength and fracture energy of concrete in seaw ater[C]∥CARPINTERI A,GAMBAROVA P,FERRO G,et al.Proceedings o f Fram cos-6 Fracture M echanics of Concrete and Concrete Structures,Catalina,Italy：Taylor&Francis,2007：213-217.

[13]ROELFSTRA P E,W ITTMANN F H.Numerical method to link strain so ftening with failure o f concrete[C]∥WITTMANN F H.Fracture Toughness and Frac ture Energy of Concrete,Am sterdam：Elsevier,1986：163-175.

[14]RILEM Recommendation FMC-50.Determination of fracture energy o f mortar and concrete by means of three-point bending test on notched beams[S].M ateria ls and Structures,1985,18(106)：285-290.

[15]RILEM Recommendation AAC 13.1.Determ ination of the specific fracture energy and strain so ftening of AAC,RILEM technical recommendations for the testing and use of construction materials[S].E&FN Spon,1994：156-158.

[16]WITTMANN F H,FELTZUNG F,ZHAO T J.Shrinkage mechanisms,crack formation,and service life of reinforced concrete structures[C]∥JIN W L,UEDA T,BASHEER M.Proceedings of International Conference of Concrete Structures,H angzhou,China：Zhejiang University Press,2008：52-63.

[17]ZHAO T J,SUN Z W,ZHANG P.Moisture content,strength and fracture energy of concrete[C]∥XU B,XIAO Y,RU J P,et al.Proceedings of the 10th International Symposium on Structural Engineering for Young Experts,Changsha,China：Science Press,2008：1745-1751.