静水中自由船模拖曳CFD模拟方法研究
吴乘胜,陈 雄,孙立宪,顾 民,朱德祥
(1中国船舶科学研究中心,江苏 无锡 214082;2上海市计算技术研究所,上海 200040)
静水中自由船模拖曳CFD模拟方法研究
吴乘胜1,陈 雄1,孙立宪1,顾 民1,朱德祥2
(1中国船舶科学研究中心,江苏 无锡 214082;2上海市计算技术研究所,上海 200040)
基于RANS方程结合VOF处理自由面,建立了自由船模拖曳的数值模拟方法,并用于数条水面船模阻力的数值计算。数值模拟结果与模型试验的比较表明:在全Fr范围内,阻力数值计算结果与模型试验相差2%~3%之内,较拘束模计算准确度大为提高;兴波计算结果同样有明显改善;船模姿态的计算结果与模型试验也比较接近。建议在进行中高速水面船自由面绕流问题的数值计算时,使用自由模方法模拟。
自由船模;数值模拟;RANS方程;VOF方法
1 引 言
船舶阻力的准确预报长期以来一直是船舶研究设计人员关心的问题之一,也是CFD工作者关注的问题之一。为了运用CFD技术准确预报船舶/船模阻力,近年来,国内外研究人员做了大量的工作[1-5],包括对计算区域、网格划分、湍流模型以及自由面处理等等各方面的研究,这些研究工作在一定范围内大幅提高了CFD预报精度。
众所周知,水面船绕流问题的一个重要特点是自由面的影响。正是由于自由面的存在,给水面船绕流数值模拟带来了一些困难。首先是自由面的模拟,经过研究人员长期的努力,目前已经有诸如VOF、Level-set等成功的算法得到了广泛的应用,并且不断有新的算法出现。其次,水面船航行会对其附近流场产生影响,使得压力场和剪应力场发生变化,这些变化反过来又会影响船舶的航行姿态,即产生升沉和纵倾;航行姿态的变化又会影响船舶附近流场及其所受阻力。这些影响及变化是相互耦合的。
在早期的水面船CFD计算中,一般都不考虑船舶姿态变化的影响。对于大多数低速船(Fr在0.2左右或更低)来说,不考虑船舶航行姿态的变化进行CFD计算也是合理的,因为模型试验和数值计算经验都表明,此时船舶航行姿态的变化很小,尚不足以对阻力、兴波等产生明显影响。但对于中高速船来说,再不考虑船舶航行姿态的变化就不太合理了,因为此时船舶的升沉、纵倾较大,将会对阻力、兴波等产生比较明显的影响。作者在此前的研究工作中[6],曾经针对ITTC标模DTMB5415,进行了Fr=0.10~0.45时船模的阻力、兴波等的数值计算,并与模型试验进行了全面的比较。CFD计算与模型试验结果的对比说明:在航速较低时(Fr<0.25),船模的升沉和纵倾都很小,对阻力的影响也很小,不高于2%,在模型试验或数值模拟的不确定度范围之内;而在航速较高时(Fr>0.25),船模的升沉和纵倾对阻力的影响则比较明显,最大达到约20%,此时如再不考虑升沉和纵倾的影响显然是不合理的。
为了使较高航速下水面船CFD计算结果更为准确,研究人员采取了各种方法。有的根据模型试验或其它手段获得的数据对计算结果进行修正[6];或是在数值模拟时给定船模的升沉和纵倾再进行计算[7,9]。这类方法的主要问题在于要预先知道船模的升沉和纵倾。截止目前,这些方法仍被较广泛使用。近年来,CFD技术的发展也使得自由船模拖曳的模拟成为可能,并得到了一定范围的应用[8-9];Gothenburg2010 CFD Workshop的算例中也有要求自由模模拟。
本文基于 RANS(Reynolds Averaged Navier-Stokes)方程结合 VOF(Volume of Fluid)方法处理自由面,建立了自由船模拖曳的数值模拟方法,并用于数条水面船模阻力的数值计算。数值模拟结果与模型试验的比较表明:在数值模拟的全Fr范围内,阻力计算结果与模型试验相差最大不超过2%~3%,在中高速情况下,较拘束模计算准确度大为提高;兴波计算结果同样有较大改善;船模姿态(升沉和纵倾)的计算结果与模型试验也相当接近。
2 数学模型及控制方程
在本文的水面舰船自由面绕流问题的数值模拟中,将自由面流动作为两相流(水和空气)来处理,自由面就是水和空气的交界面;由于流场中流体流动速度与音速相比很小,因此将水和空气都作为不可压缩流体处理;自由面使用VOF方法处理。
不可压缩流体流动的连续性方程为:

对于水面船自由面绕流问题这种两相流,水与空气的质量都应该是守恒的。由于流体的不可压缩性,可以用体积分数写为:

计算区域内的每个控制体积都由水和/或空气充满,它们的体积分数之和应为1,即:

其中α表示体积分数,下标a和w分别代表空气和水。
两相流同样要满足动量守恒方程:

其中:ρ为流体密度;μ是粘性系数;g→为重力加速度;p是压力;F→为采用随体坐标系模拟运动而产生的非惯性项,其表达式为:

数值模拟中使用的RNG k-ε二方程模型是船舶CFD计算中经常使用的一种湍流模型,其具体形式可以参阅相关文献。
3 数值计算
3.1 计算区域及网格划分
由于本文的CFD计算问题具有对称性,因而在数值计算时只需计算一半区域。计算区域及网格划分参考了文献[4-6]的研究成果。
计算区域如图1所示,其边界包括以下几个部分:
a.前端—模型首部前约1.2LWL处;
b.后端—模型尾部后约2.5LWL处;
c.侧边界—模型侧方约1.3LWL处;
d.上边界—水线以上约0.3LWL处;
e.下边界—水线以下约1.3LWL处;
f.对称面—模型中纵剖面的延展面;
g.舰船模型表面。
计算中使用的网格为H-O型结构化网格(纵向H型、横向O型),计算区域的网格单元总数约为50万左右。网格划分的基本原则为:舰船模型首部和尾部网格适当加密,中部网格较为稀疏;在模型表面附近网格加密,其中第一层网格间距根据y+确定(y+平均约为50左右);自由表面附近网格也适当加密。图2给出了舰船模型表面网格划分示意图。
3.2 边界条件及初始条件
数值计算中,边界条件的具体设置如下:
a.在入口边界上,根据舰船模型运动速度和自由面位置,给定入口流动速度以及水和空气的体积分数;
b.出口边界距离船模足够远,其压力分布设置为静水压力;
c.在舰船模型表面,引入标准壁面函数;
d.在对称面上,满足对称条件。
以均匀流场作为数值计算的初始条件。

3.3 离散格式及求解
控制方程使用有限体积法(Finite Volume Method,FVM)离散,其中对流项采用二阶迎风差分格式,扩散项采用中心差分格式。离散得到的差分方程组具有高度耦合性和非线性,使用SIMPLE(Semi-Implicit Method for Pressure Linked Equations)方法求解,使用多重网格(Multigrid)技术加速收敛。
4 船模升沉和纵倾模拟
水面舰船模型拖曳前进时,会对其周围流场产生影响,使压力场和剪应力场发生变化,也就使船模所受的力和力矩发生变化:

根据牛顿第二定律,船模运动的六自由度控制方程表达式如下:


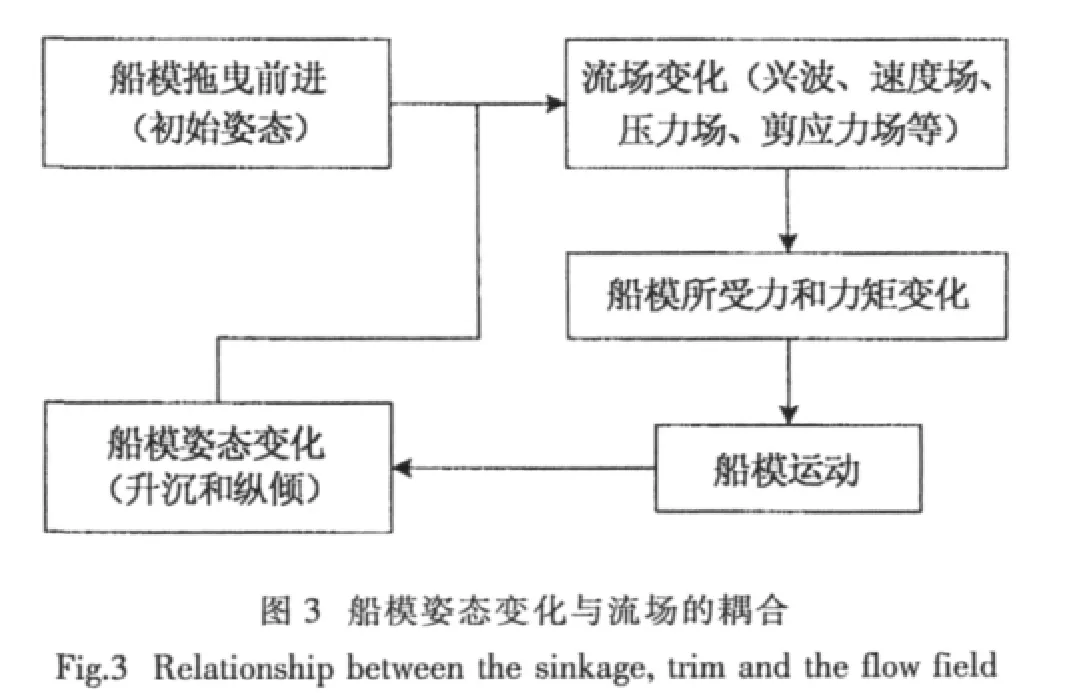
在数值模拟中,作用在船模上的力和力矩可由(6)、(7)两式得到,其运动的速度、角速度及位置、姿态等可以通过(8)、(9)两式求解、积分得到。船模姿态变化与流场之间的耦合如图3所示。这个耦合迭代过程使得数值模拟足够长时间后,力和力矩相对平稳(或在某个值附近振荡),船模运动至某个姿态也会相对稳定(或在某一姿态附近振荡),这一姿态也就是船模拖曳前进的平衡姿态。
5 算例简介
本文首先针对水面船模DTMB5415进行模拟,计算结果与模型试验及拘束模模拟的结果进行全面的比较分析,对本文的模拟方法进行了验证。然后对三艘水面船模型进行了计算,并与模型试验进行了比较,进一步验证了本文的模拟方法。
DTMB5415船模及三艘水面船模型M1、M2和M3的主尺度列于表1中。在低速工况下(Fr<0.20),船模的升沉、纵倾都很小,对阻力、兴波等的影响微乎其微,因而仍使用拘束模方法模拟;在中高速工况下(Fr>0.20),则使用自由模方法进行模拟。
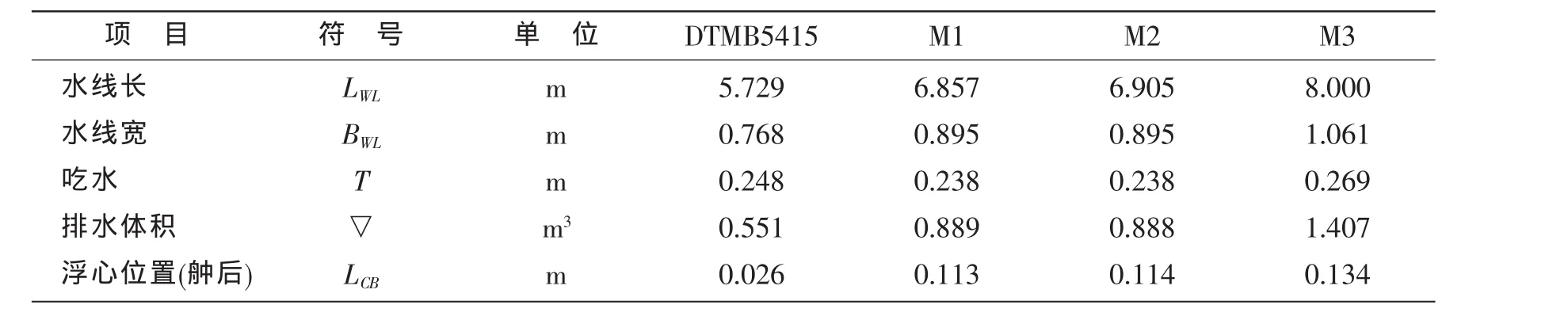
表1 船模主参数Tab.1 Main particulars of the ship models
6 计算结果及分析
CFD计算中,坐标轴的定义为:流动方向为X轴正向,Y轴正向指向舰船的右舷,Z轴正向垂直于水平面向上,坐标原点位于船模横中剖面、对称面和设计水线面的交点。结果处理中,无量纲量如傅汝德数Fr、雷诺数Re的定义如下:

其中,V 为船模速度,ρw,μw分别为水(15°C 淡水)的密度和粘性系数。
总阻力系数CT、摩擦阻力系数CF和剩余阻力系数CR的定义如下:

其中,R为船模阻力,SW为船模湿表面积,(13)式为计算相当平板的摩擦阻力系数的Prandtl-Schlichting公式。
无量纲化的升沉和纵倾定义为:

其中δz和θ分别为船模的升沉量(上升为正)和纵倾角(尾倾为正)。波形中波面升高的无量纲化形式为:

其中z为兴波波面升高。
在本文的数值模拟中,船模有二自由度运动,即升沉和纵倾。图4给出了数值模拟中一个典型的垂向力时间历程曲线,图中虚线表示船模所受重力。在实际中,垂向力应该与船模重力平衡,而图中数值计算的垂向力正是在船模重力附近小幅振荡。图5则给出了船模升沉量的时间历程。从图中可以看出,船模的确是运动至某一姿态后相对稳定,在平衡位置附近小幅振荡。纵摇力矩和纵倾角的时间历程与上述情形类似。以上这些都说明了本文的数值模拟方法是稳定可行的。

6.1 DTMB5415计算结果
表2和图6给出了船模DTMB5415的阻力数值计算结果,表中同时给出了拘束模计算结果和模型试验结果。从图表中可以看出,在数值模拟的全航速范围内,阻力的计算结果与模型试验相当吻合,二者之间的差别最大不超过2%~3%,基本上都在模型试验的不确定度范围之内[10];与拘束模数值模拟相比,在速度较高时,本文的数值方法计算得到的船模阻力准确度大为提高。图7则给出了DTMB5415的总阻力系数和剩余阻力系数,图中同时给出了CSSRC和IIHR(Iowa Institute of Hydraulic Research)的模型试验结果。从图中可以看出,本文数值计算结果与国际知名研究机构的模型试验结果也相当吻合。
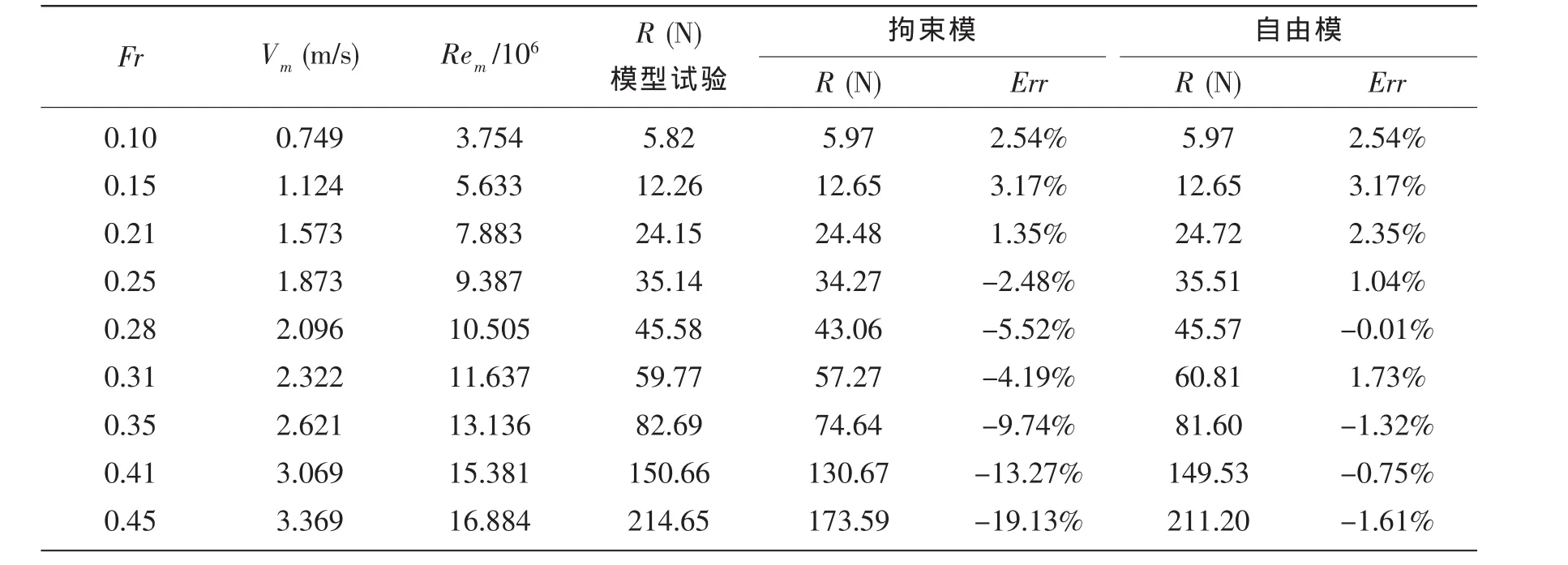
表2 DTMB5415阻力计算结果Tab.2 Computed resistance of DTMB5415

表3给出了DTMB5415升沉和纵倾的数值计算结果,表中同时给出了CSSRC和IIHR的模型试验结果;图8则给出了船模的无量纲化升沉、纵倾及其与模型试验结果比较(图中左侧为无量纲化升沉,右侧为无量纲化纵倾)。从图表中可以看出,数值计算的船模升沉、纵倾与模型试验有一定差别,但总体上符合尚好,且二者的趋势是一致的。考虑到模型姿态变化不是很大,特别是纵倾角比较小(最大不过1°左右),同时自由船模拖曳的数值模拟进行得还相当少,数值模拟的船模姿态能与模型试验符合到这种程度亦属不易。
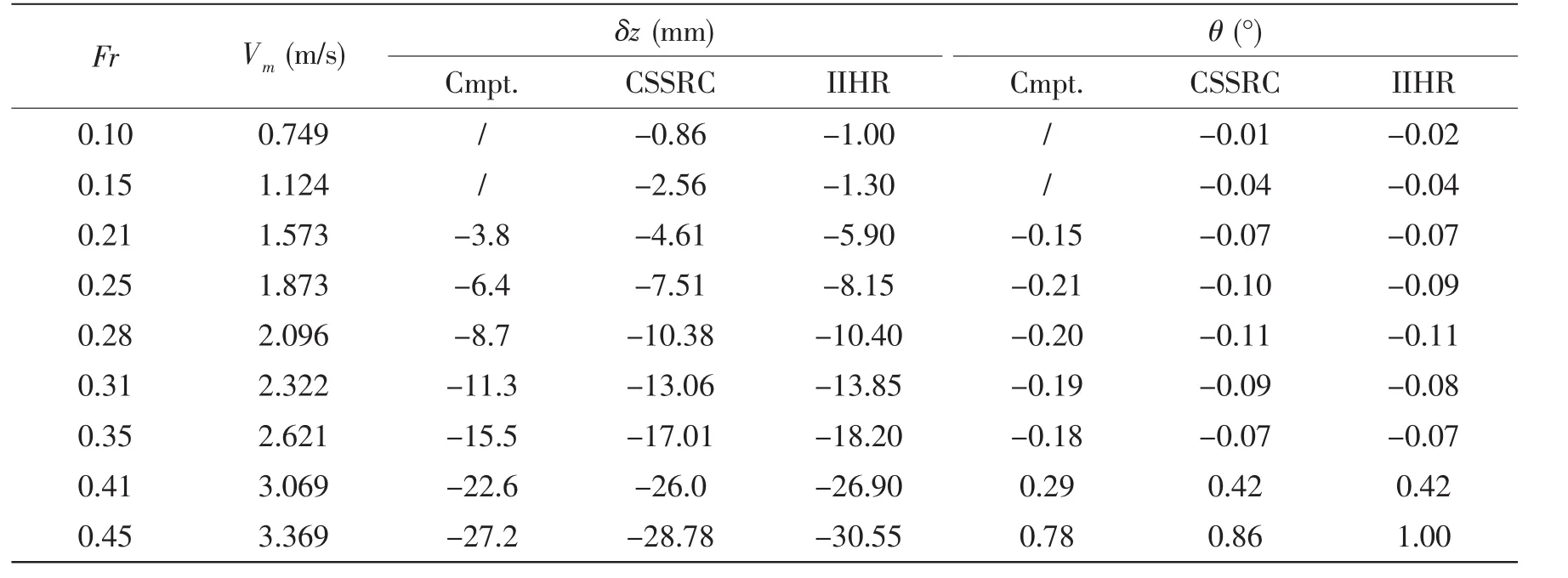
表3 DTMB5415升沉、纵倾计算结果Tab.3 Computed sinkage and trim of DTMB5415

图9给出了Fr=0.41时,y=0.172LPP纵切面的波形数值模拟结果,图中同时给出了拘束模模拟结果和模型试验结果。从图中可以看出,相对于拘束模方法,自由模方法的兴波模拟结果有较为明显的改善,特别是在船体舯部的波谷处,同时船体后方波峰、波谷的模拟结果也有所改善;x/LPP=1.5之后的波形计算结果与模型试验差别明显,是由于为了尽量减小出口边界的影响,此处的网格逐渐稀疏,数值粘性增大所致。
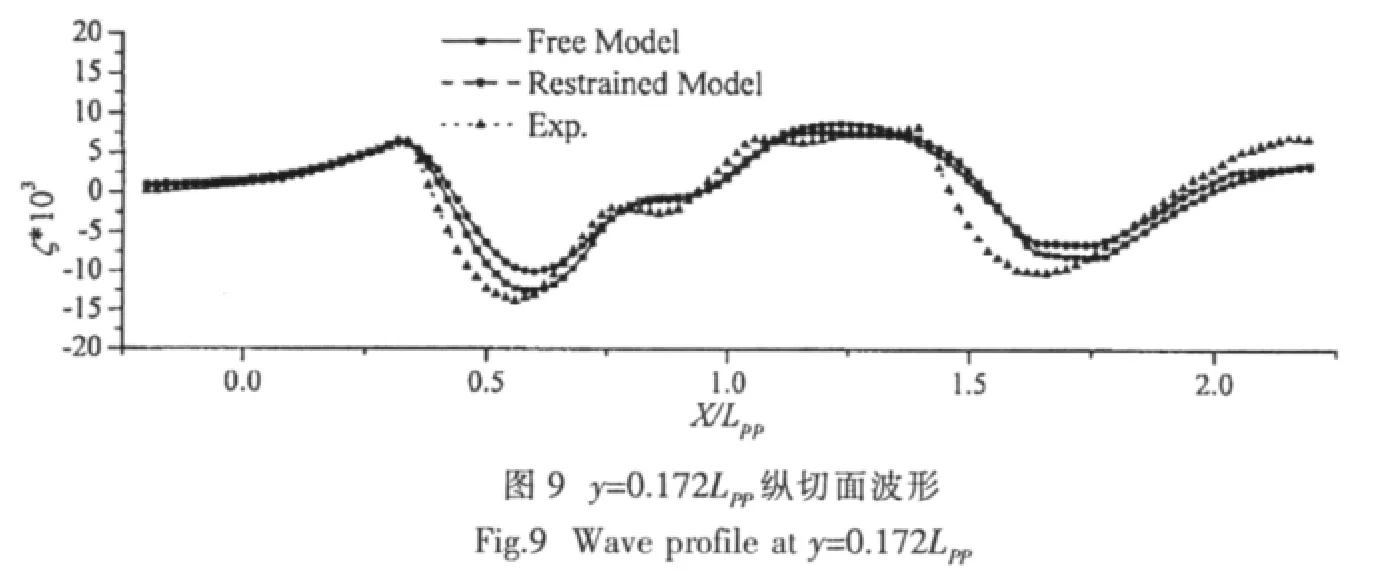
由以上数值模拟结果可以看出,本文建立的自由模拖曳的数值模拟方法,相对于拘束模方法,在中高速情况下,阻力、兴波的计算结果都有明显改善,同时船模姿态的模拟结果与模型总体上符合尚好。
至此,本文的自由船模拖曳CFD模拟方法得到了较为完整的模型试验验证。由此,建议在进行中高速水面船(Fr>0.20)自由面绕流问题的数值模拟时,应尽量采用自由模方法。以下将本方法用于三艘水面船模的阻力及姿态预报,并通过与模型试验的比较,进一步验证本文的数值方法。
6.2 船模 M1、M2、M3计算结果
表4给出了船模M1、M2和M3的阻力数值计算结果,表中同时给出了模型试验结果(其中下标cmpt代表计算,exp代表模型试验)。从表中可以看出,在数值模拟的全航速范围内,阻力的计算结果与模型试验相当吻合,二者之间的差别最大不超过2%~3%,基本上也都在模型试验的不确定度范围之内。图10-12则给出了各船模阻力及阻力系数的计算结果与模型试验结果比较(各图中左侧为阻力曲线,右侧为阻力系数曲线)。

表4 船模阻力计算结果Tab.4 Computed resistance of the ship models
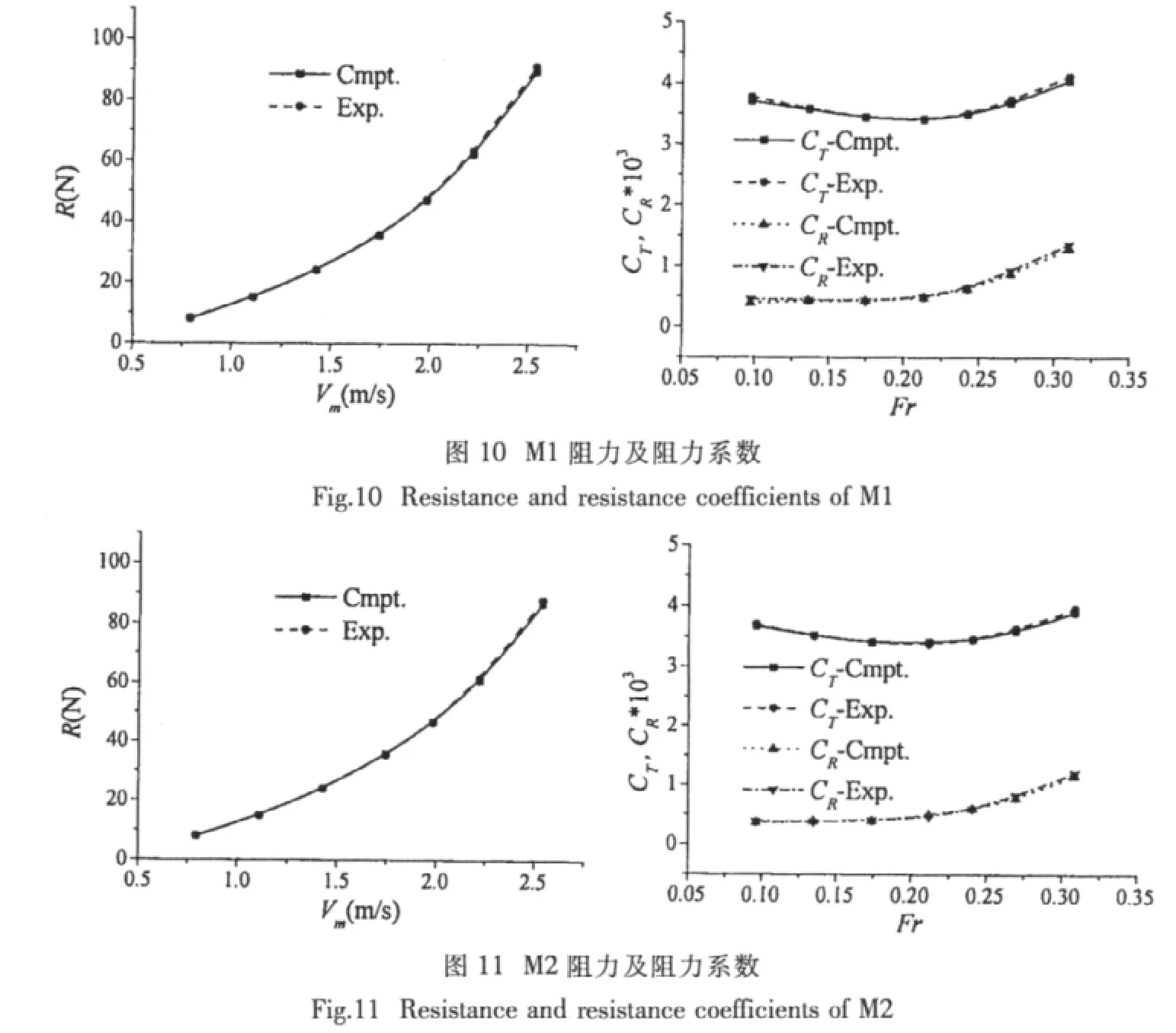


表 5 船模升沉(单位:mm)、纵倾(单位:°)计算结果Tab.5 Computed sinkage(mm)and trim(°)of the ship models

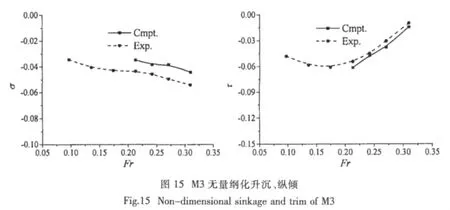
表5给出了船模M1、M2和M3升沉和纵倾的数值计算结果,表中同时给出了模型试验结果;图13-15则给出了各船模的无量纲化升沉、纵倾及其与模型试验结果比较(各图中左侧为无量纲化升沉,右侧为无量纲化纵倾)。从图表中可以看出,数值计算的各船模升沉、纵倾与模型试验有一定差别,但总体上符合尚好,且二者的趋势是一致的。考虑到模型姿态变化不是很大,特别是纵倾角相当小(最大不过0.1°左右),数值模拟的船模姿态能与模型试验符合到这种程度实属不易。
由以上三艘船模的数值模拟结果可见,本文建立的自由船模拖曳的CFD模拟方法,确实适用于中高速水面船自由面绕流问题,数值计算得到的船模阻力与模型试验相当吻合,船模姿态的模拟结果与模型试验总体上也符合较好。
7 结 语
根据上述几艘水面船模型的计算结果,说明采用本文的数值方法能够进行静水中自由船模拖曳前进的模拟:
a.在数值模拟的全航速范围内,阻力的计算结果与模型试验相当吻合,二者之间的差别最大不超过2%~3%,基本上都在模型试验的不确定度范围之内,相对于拘束模方法数值模拟,在速度较高时,阻力预报的准确度大为提高;
b.对于航行姿态的模拟,数值计算的各船模升沉、纵倾与模型试验有一定差别,但总体上符合尚好,且二者的趋势是一致的;
c.兴波的模拟结果也有明显改善。
因而,建议在进行中高速水面船自由面绕流问题的数值计算时,应采用自由模方法模拟。
本文的工作仅是针对裸船体的,今后将进一步针对全附体船进行模拟,并考虑将本方法应用到水面船自航数值模拟中。
[1]Svennberg S U.A test of turbulence models for steady flow around ships[C]//Proc.of Gothenburg 2000-A Workshop on Numerical Ship Hydrodynamics.Gothenburg,Sweden,2000.
[2]张志荣,李百齐,赵 峰.船舶粘性流动计算中湍流模型应用的比较[J].水动力学研究与进展,2004,19(5):637-642.
[3]张志荣.水面舰船综合性流场的实用化CFD研究[D].无锡:中国船舶科学研究中心,2004.
[4]黄少锋.带自由面肥大型船舶CFD实用化研究[D].无锡:中国船舶科学研究中心,2006.
[5]黄少锋,徐 杰,马 峥.散货船阻力预报的数值试验研究[C]//第九届全国水动力学学术会议及第二十二届全国水动力学研讨会.成都,2009.
[6]吴乘胜.ITTC标模DTMB5415阻力CFD计算[R].无锡:中国船舶科学研究中心科技报告,08299,2008.
[7]Maki K J,et al.Resistance predictions for a high speed sealift trimaran[C]//Proc.9th Int.Conf.Numerical Ship Hydrodyanmics.Ann Arbor,MI,USA,2007.
[8]Azcueta R.Steady and unsteady RANSE simulations for littoral combat ships[C]//Proc.25th Symp.Naval Hydrodynamics.St.John’s Newfound Land,Canada,2004.
[9]Miller R,et al.Resistance predictions of high speed mono and multihull ships with and without water jet propulsors using URANS[C]//Proc.26th Symp.Naval Hydrodynamics.Rome,Italy,2006.
[10]吴乘胜,杨 磊.水面船模兴波、阻力CFD不确定度分析[C]//第九届全国水动力学学术会议及第二十二届全国水动力学研讨会.成都,2009.
[11]The Resistance Committee-Final Report and Recommendations to the 24th ITTC[C]//24th ITTC.Edinburgh,UK,2005.[12]The Resistance Committee-Final Report and Recommendations to the 25th ITTC[C]//25th ITTC.Fukuoka,Japan,2008.
Numerical simulation of free ship model towed in still water
WU Cheng-sheng1,CHEN Xiong1,SUN Li-xian1,GU Min1,ZHU De-xiang2
(1 China Ship Scientific Research Center,Wuxi 214082,China;
2 Shanghai Insitute of Computing Technology,Shanghai 200040,China)
Numerical simulation of free ship model towed in still water is carried out in this paper by solving RANSEs with VOF method for the treatment of free surface.The computed results of resistance,sinkage and trim for several surface ship models are compared with those of experiments and show quite good agreement.The prediction of resistance and wave profile is improved quite a lot as compared with that by restrained model simulation.
free ship model;numerical simulation;RANSE;VOF method
U661.3
A
1007-7294(2010)08-0823-11
2010-02-30
吴乘胜(1976-),男,博士,中国船舶科学研究中心高级工程师。

