图像压缩技术JPEG的分析

郑崴,苗青林

（河南科技学院,河南新乡453003）

随着数字图象技术应用的日益广泛,多媒体技术、电话会议以及高清电视的普及,都可以给工作生活带来丰富的图象信息.由于图象信息会占用大量的通信带宽和存储空间,因此图象信息越多,对带宽和存储空间的要求也就越高.一张高为297 mm、宽为210 mm的照片,利用一台300 DPI的彩色扫描仪将其转换为数字图象进行存储,则需要26 M的存储空间.可以看出,对高效率的图象压缩技术的需要在数字图象应用日益广泛的今天是非常迫切的.

现在已经有多种非常成熟的图象压缩技术,而这其中最常用的不外乎Joint Photographic Experts Group发布的JPEG2000和JPEG这两种图象压缩标准.虽然两种标准都可以实现数字图象的压缩,但是它们使用了两种截然不同的实现方法.JPEG标准是基于离散余弦变换,这是一种类似与傅立叶变换的数学变换方法[1],并且是一种有损的图象压缩技术[2].而JPEG2000标准的提出主要是为了实现图象的无损压缩,并且利用JPEG2000实现的图象压缩获得的图象效果一般情况下是好于JPEG标准的.尽管如此,由于JPEG2000是基于小波变换的一种压缩技术,因此无论是在硬件上还是软件上其实现起来,都要难于JPEG[3].所以,在一些处理器速度比较低的移动设备中,JPEG的应用更加广泛,并且基于模块编码算法的JPEG也更加的容易实现.所以,这种基于模块编码的图象压缩技术的关键就在于研究快速的算法的实现以求减少图象信息处理过程的计算量.

1 JPEG标准的优点

JPEG（Joint Photographic Experts Group）全称为联合图像专家组,建立于1986年.在1992年,联合图像专家组发布了图象压缩标准JPEG,直到现在,JPEG标准仍然广泛的应用于图象压缩领域.由于JPEG标准的优越性,它成为在通信中尤其是互联网中最常用的图片格式.JPEG是一种有损图象压缩方法,也就是说,JPEG将图象信息中的多余的信息量和对视觉影响不明显的信息量删除掉来达到压缩的目的.因此,如果压缩比过大,则压缩后的图片效果就会比较差.尽管如此,在存储空间有限的情况下,JPEG仍然有其应用的价值.一般的JPEG编码器会提供从10：1到40：1的压缩比,当然,压缩比越高,则得到的压缩图象的质量会越差,而压缩过程中丢失的信息是对视觉影响不明显的低频部分,而视觉比较敏感的高频部分则会被保存下来[4].图1是一个JPEG图象编码标准的流程,而解码部分是编码部分的逆过程.

图1 一般的JPEG标准

近来,基于小波变换的JPEG2000图象压缩标准得到了广泛的应用,由于JPEG2000相较于JPEG可以得到较高的压缩比和较高的图象效果,在一定程度上,有取代JPEG的趋势.但是,JPEG由于实现简单、计算量小、占用内存少等优点,在一些特殊的场合,尤其是在计算速度较慢的移动设备中,JPEG相比较于JPEG2000来说更加的适用.所以,基于对图象模块编码的以JPEG为代表的图象处理方法仍然具有光明的前途,并且广泛的应用与互联网与图象存储中,尤其是在移动电话越来越流行的今天,JPEG的这些优点决定了其无可替代的地位.此外,由于JPEG出色的压缩图象质量和迅捷的下载速度,现在常用的各种浏览器全部支持JPEG格式的图象文件.

2 图象压缩中的DCT与DCT算法

压缩是出于对存储和数据传输的目的,对于信息进行重新组合的过程[5],与一般的数据压缩相比较而言,图象压缩具有其自身特有的压缩技术.一般数据的压缩通常都是无损的,因为这个时候一个数据的错误都可能导致最后的结果出现错误,而图象压缩恰恰相反,图象中的冗余信息的比重是相当大的,因此,在一些即时更新的图片网站中,图象压缩是必不可少的过程.图象压缩的目的就是去除原始信息中冗余的信息和对图象效果影响较少的这部分数据,而DCT变换的作用就是将图象中各个频率的信息区分开来.再将对视觉敏感的高频部分信息保留下来,而对视觉无法察觉的低频部分在数值上设为零从而达到图象压缩的目的.这个过程在图象处理中称之为量化,其实就是删除原始图象数据中的冗余部分.由此可以看出,DCT在图象压缩技术中,尤其在JPEG中的重要地位,没有DCT对数据进行区分,图象的压缩就无法实现.

DCT在JPEG当中扮演着重要的作用,而且DCT应用于图象压缩中是以对图象模块编码处理为基础的,其处理过程就是将一张图片划分为许多小的模块,再按自左至右,自上而下的顺序对这些模块分别进行DCT运算.实际上,离散余弦变换一共有四种形式,而常用于图象压缩的离散余弦变换是第二种形式,多表示为DCT-II型,其主要包括式（1）、（2）[1],其中p表示原始图象矩阵中的一个象素点.

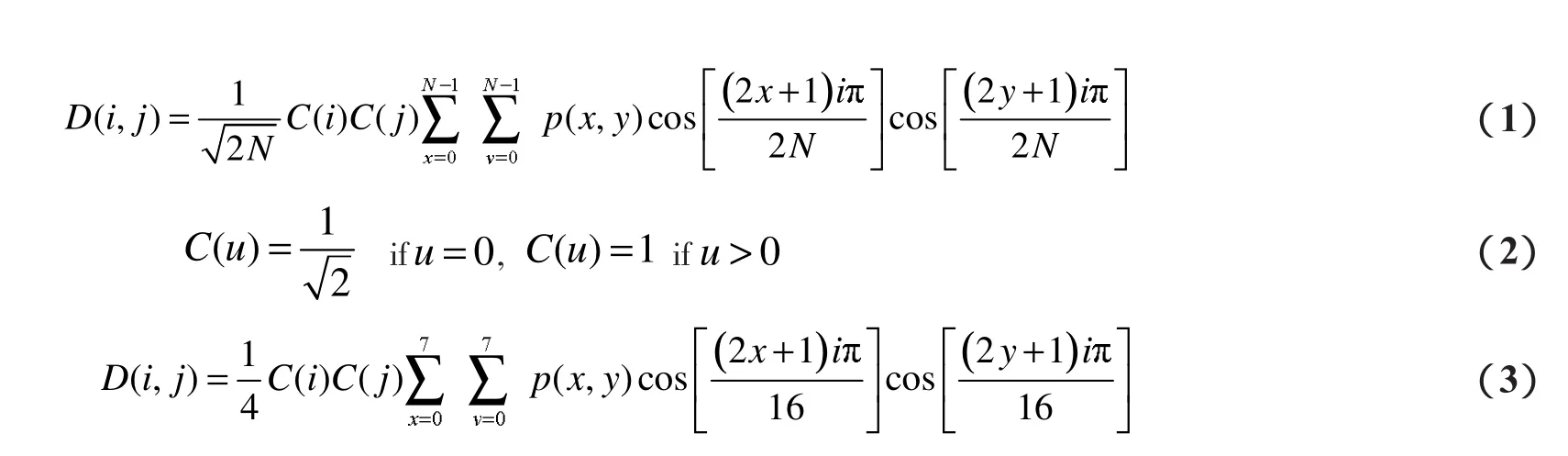
N表示一个DCT模块的标准.一般情况,标准的DCT模块的标准多为N=8（JPEG,H.263）[2,5]或者N=16（MPEG）[6].如过一个基于的DCT模块的算法,其中x和y的取值应该是由1到7,以保证符合DCT模块的标准.将式（2）带入式（1）可得式（3）,可以得到一个变换后的矩阵 T,再经过式（4）[1]进行计算,便可得到一个完成DCT变换的8×8的矩阵,其中M表示原始图象矩阵中的一个需要进行处理的8×8矩阵模块,T’表示矩阵T的转置矩阵.

需要注意的是,因为这里用到的是一个8×8的DCT矩阵模块,所以在进行变换之前需要先把一个a*b大小的原始图象平均的化为若干个8×8的模块.此时,如果a和b能够被8整除,称之为完美矩阵模块.当a和b不能被8整除时,则需要补上值为0的象素点以使得图象能够达到完美矩阵模块来进行变换.

这种基于DCT模块编码的图象压缩技术更容易在一些低端处理器上实现,而这种图象压缩技术研究的核心问题就是如何找到快速的DCT算法.经过DCT处理,可以将一张图片的低频部分放在一个DCT模块的左上角,而高频部分则放在模块的右下角,这样,通过变化可以将一张图片的各个不同的能量部分区分开来以方便进行量化压缩[7].因此,无论是在硬件实现还是软件实现上,都有很多的快速DCT的算法.有些快速DCT算法是利用了离散傅立叶变换（DFT）和DCT之间的关系而得到的,所以已有的快速FFT算法在这里也可以做为提高DCT处理的速度,比如FFT[8-9]和Walsh-Hadamard transform（WHT）[10-11].但是由于本身DFT的复杂性,这种类型的快速DCT算法在减小计算量提高运算速度上的作用是有限的；还有一些快速DCT算法是通过对DCT矩阵进行因数分解,将复杂的计算变为简单的三角函数计算,在一定程度上减少DCT处理中的计算量,使其容易实现.如图2中的算法结构,就是基于这种思想的一种算法.这些算法的主要思想就是尽量减少DCT中的乘法次数,因为乘法会占用大量的处理器资源.

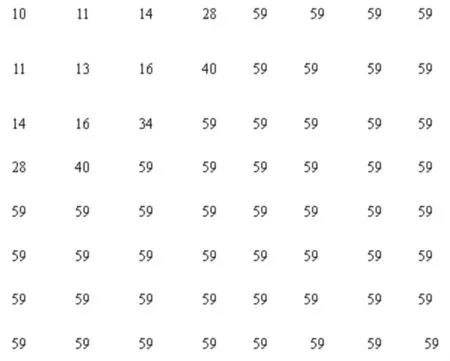
图2 量化表

3 量化

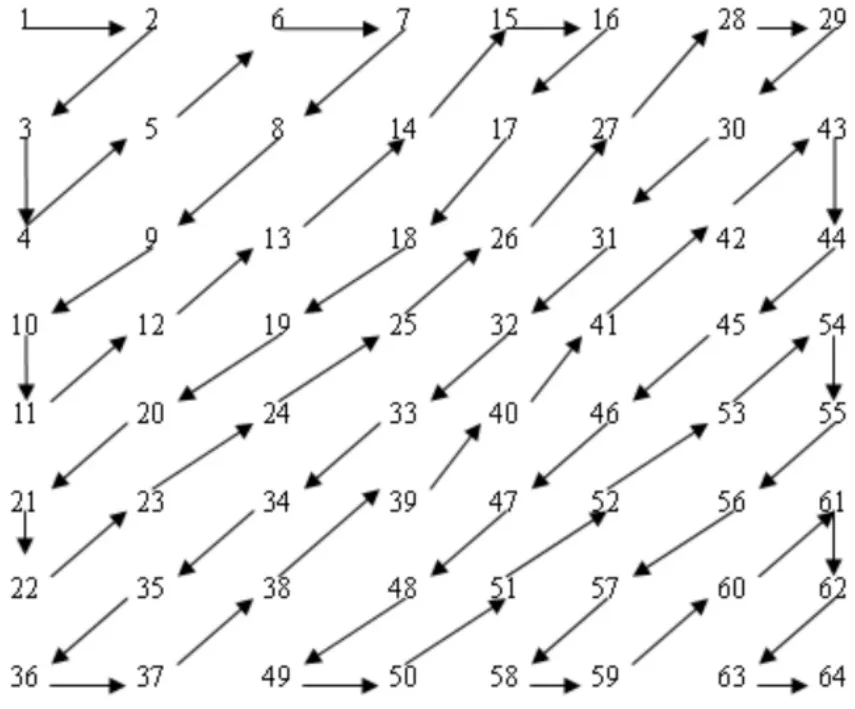
图3 Z顺序表

实际上,图象的多余信息的压缩完全是由量化部分完成的.在JPEG标准中,当DCT变化执行完毕后,图象中的信息根据各自不同的频率分布在不同的位置上.这时,在根据不同的压缩要求将这些象素值进行四舍五入计算,再与标准量化表进行相乘,之后变得到量化后的值.如设x为DCT变化后的一个象素点的值,q为使用的量化表的规格,常用的为8×8标准的量化图,则由公式可得量化后的结果.图2为常用的一个标准量化表.

4 编码

在JPEG标准中,编码部分的功能是将DCT和量化后的图象信息变为数字信息.在基于模块化图象压缩的JPEG标准中,最常用是霍夫曼编码,在编码过程中需要按照一定的顺序进行处理,这种顺序称为“Z顺序”,如图3所示,图中的数字代表这量化后的图像点的系数.一般情况下,左上角的系数代表这一个8×8模块的交流值,而其他系数代表这模块的直流值,经过编码后,不同的直流值和交流值则会被变化为不同的霍夫曼码.

5 结语

在对JPEG的各个模块进行分析的基础上,着重分析了DCT在JPEG标准中的所起到的分离信息量的作用,可见DCT是JPEG能够实现图像压缩的基础,而快速的DCT算法可以提高JPEG编码器的计算速度和压缩效率,而在量化和编码的部分主要利用图表法来实现,因此要想提高图像压缩的效率只有考虑快速DCT的算法来实现.

[1]Gregory K W.The JPEG still picture compression standard[J].IEEE Transactions on Consumer Electronics,1992,1（38）：777-789.

[2]AndrewB.Watson.Image compressionusingthe Discrete Cosine Transform[J].Mathematical Journal,1994,4（1）：81-88.

[3]ZixiangXiong,KannanRAchandran,Michael T,et al.Acomparative studyofDCT-andwavelet-basedimage coding[J].IEEE Transactions onCircuits andSystems forVideoTechnology,1999,5（9）：202-207.

[4]Shao G F,Li Z S,Zhang H,et al.Image Fusion Based on Human Vision Perception[C].Shanghai：Proceedings of the Third international Conference onMachine LeaningandCybernetics,2004：26-29.

[5]Li J.Image compression-the mathematics ofJPEG2000[C].MSRImodernsignal processingseries,2000.

[6]AhemdN,NatarajanT,RaoKR.Discrete Cosine Transform[J].IEEETransactions onComputer,1974,23：90-93.

[7]ChenWH,PrattWK.Science adaptive coder[J].IEEETransactions onCommunications,1984,32：225-232.

[8]RaoKR,YipP.Discrete Cosine Transform[R].NewYork：Academic,1990.

[9]PennebakerWB.JPEGStill Image DataCompressionStandard[C].NewYork：VanNorstrandReinhold,1993.

[10]ITU-T.MPEG-2 video[S].ITU-TRecommendationH.262-ISO/IEC13818-2,1995.

[11]ITU-T.Videocodingforlowbitrate communication[S].ITU-TRecommendationH.263,1995.