有效估计罗兰C天波参数的方法
李 睿,田孝华,王维康
(空军工程大学电讯工程学院,西安 710077)
0 引言
罗兰C接收机通过测量不同发射台发射的地波信号到达接收机的时间差计算双曲线位置线,而后解算目标位置进行定位。时间差的测量使用脉冲相位技术,即以地波信号载波上某一个相位零点为基准点,接收设备产生多个采样脉冲,使采样脉冲分别对准主、副台信号的基准点,测量采样脉冲的时间间隔得到时差值。理论上,基准点的最佳位置在地波载波包络上升沿上最靠近天波前沿的那个周期内,但是罗兰C接收机接收到的地波信号会不可避免地受到天波以及噪声等的影响,从而使得对准基准点时会产生误差。为了防止天波干扰,目前的接收机大多将载波第3周期末的过零点作为基准点。但是,采用固定的基准点的测量方法使得基准点处信噪比较低,受噪声干扰影响较大,制约接收机性能提高。若接收机能根据实际情况,灵活调整基准点的位置,以使得基准点处信噪比较高,就可有效抑制噪声干扰。因此,必须估计出天波的参数。基于此目标,本文提出利用代价函数估计天波参数,并利用迭代提高估计精度。
1 信号模型
为了减少天波影响,罗兰C系统对发射信号的要求是:前沿要陡、频谱要窄。因此,信号包络函数由抛物线和指数衰减曲线两部分相乘而组成。它利用抛物线迅速上升的特点,获得陡的前沿;利用指数衰减曲线迅速下降而后平稳的特点,使其频谱不太宽。其包络函数表达式为

其中:τ为信号起点到峰值点的时间。随着τ值的减小,带宽加大,一定带宽内的能量减少。一般τ的取值范围是60~75 μs。接收机接收到的罗兰C信号是由地波信号、天波信号、噪声以及干扰组成的合成信号。为便于分析,假定天波和地波具有完全相同的包络形状,只是具有不同的幅度和时间上的延迟,只受噪声干扰。因此,在时域可以将接收到的合成信号表示为
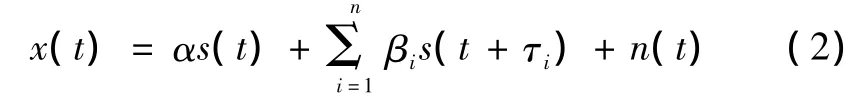
其中:x(t)是接收信号;s(t)是发射的原始信号;α是地波幅度;βi是天波幅度;τi是天波相对地波的时延;n(t)是噪声。
2 时延和幅度估计方法
从构造的信号模型可知,有3个参数需要估计,即地波的幅度,天波的幅度以及天波相对地波的时延。如果只利用一个代价函数对3个参数一起进行估计,运算量大,估计效率低。因此分3次分别对天波时延、幅度以及地波幅度进行估计。
2.1 天波时延和幅度估计
在时域利用代价函数估计天波时延,若假设时延与真实时延相差一个周期,构造的天波将与实际接收的天波接近,则代价函数的函数值相差较小。当存在噪声时,估计误差比较大。所以,考虑在频域利用代价函数对时延进行估计。若假设时延与真实时延不同,频谱的变化将比较明显,因此在频域构造代价函数,对天波时延进行估计。代价函数表达式如下:

其中:f1,f2表示接收机带宽的上下界;α0,β0是代价函数寻优开始时对地波和天波幅度的初始估计值,可以在预处理时进行估计。由于α0,β0的估计精度对最终天波参数的估计精度影响不大,因此本文不对其估计的方法进行讨论。
通过式(3)从频域估计出时延τ'后,若继续在频域利用代价函数估计天波幅度,估计结果受时延估计影响较大。当时延τ'估计不准确时,构造的信号频谱与真实的频谱无法完全重合,估计误差大。可以考虑在时域对幅度进行估计。由于信号包络不会发生剧烈变化,相差一个周期的信号变化不大,所以在时域估计幅度时,受时延估计影响小。当时延估计发生变化时,最小值位置与真实值的偏离程度不大。因此在时域构造代价函数对天波幅度进行估计。代价函数表达式如下:

其中:T是接收信号的最大时间;α0是代价函数寻优开始时的地波幅度的初始估计值;τ'是通过式(3)估计的天波时延。
2.2 地波幅度估计
估计出天波的时延和幅度后,就可在时域构造代价函数对地波的幅度进行估计,表达式如下所示:
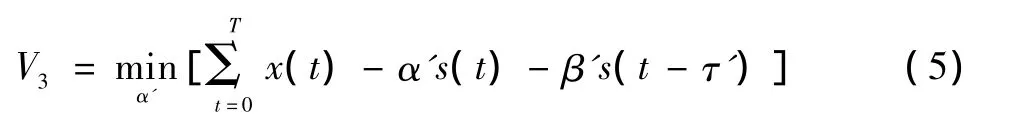
其中:T是接收信号的最大时间;β'是通过式(4)估计出的天波幅度;τ'是通过式(3)估计的天波时延。通过式(5)估计出地波幅度α'。
为了提高估计的精度,可迭代估计,式(3)~式(5)为一次迭代过程。经仿真验证,2~3次迭代就可以得到满意的估计效果。利用代价函数估计天波时延和幅度具体的估计框图如图1所示。
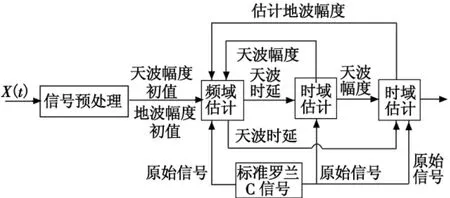
图1 天波的时延和幅度估计框图Fig.1 Diagram for estimating the time delay and fade of skywave
信号预处理的目的在于对天波、地波信号的幅度进行初步估计。根据已有的测量数据可知,天波时延范围在37.5~1500 μs,因此可以在第3周期的峰值位置粗略估计地波的幅度,再通过对比信号的最大值来粗略估计天波的幅度。经仿真检验,对天波、地波幅度初值估计的准确程度对最终的估计精度影响不大。
3 仿真分析
仿真条件为:采样率1 MHz,天波幅度相对标准罗兰C信号幅度的衰减系数为0.85,天波与地波幅度之比为12 dB、天波到达时刻相对地波时延为105 μs,信号中迭加的噪声为高斯白噪声,SNR为-10 dB(美国海岸警卫队要求的罗兰C接收机正常工作的最小信噪比指标)。
如图2所示为标准罗兰C信号,图3为迭加了天波和噪声的接收信号。可以看出,信号失真明显,直接利用图3所示波形进行周期匹配误差较大。
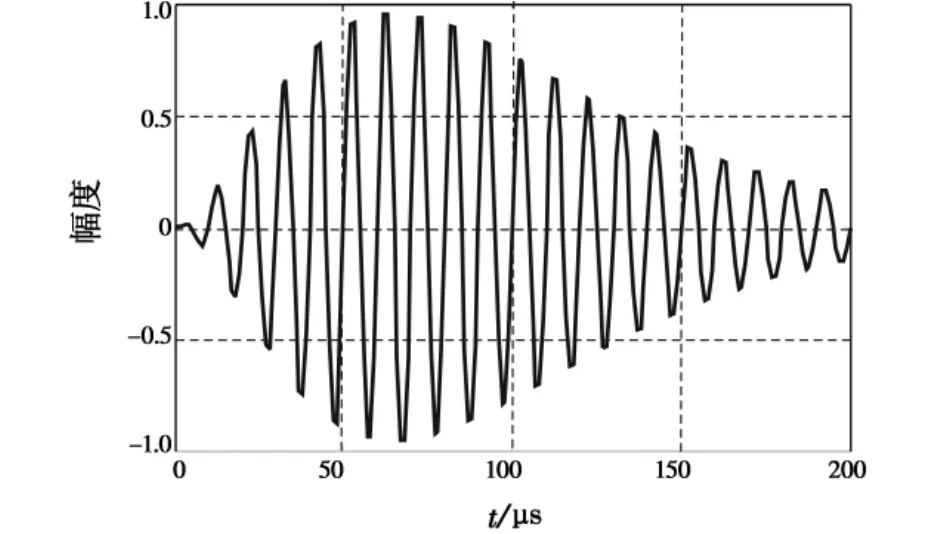
图2 原始信号波形Fig.2 Original waveform
仿真1:验证频域估计时延的有效性。
图4所示为天波幅度估计一定时在时域构造代价函数估计天波时延的输出波形。图中A点所示为真实的时延位置。可以看出,A点两侧相差一个周期的点的函数值与A点取值接近。因此,当存在噪声影响时,最小值位置可能不是在A点,估计误差较大。图5所示为天波幅度估计一定时在频域构造代价函数估计天波时延的输出波形。图中B点所示为真实的时延位置。可以看出,B点两侧相差一个周期的点的函数值与B点取值相差较远。因此,在频域构造代价函数估计天波时延受噪声影响较小,估计精度高。
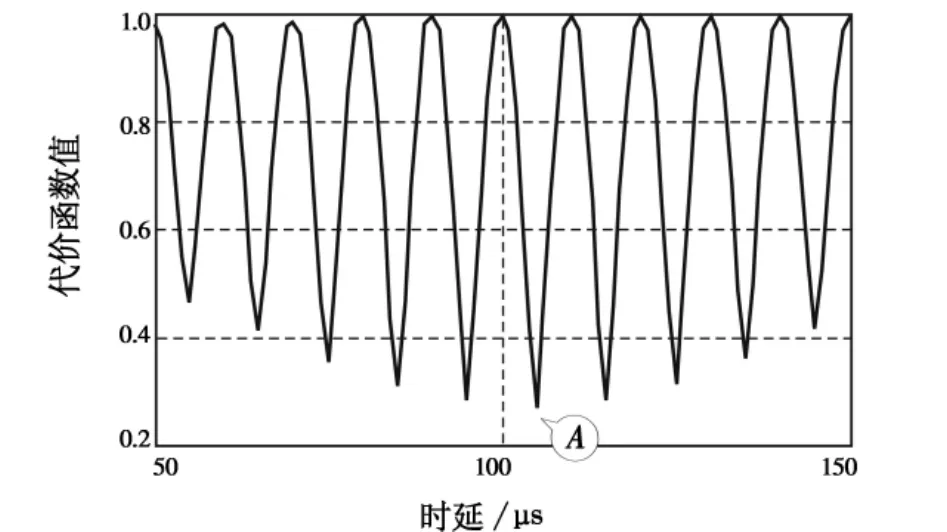
图4 幅度一定条件下对时延进行时域估计Fig.4 Estimating time delay with time-cost function under given amplitude
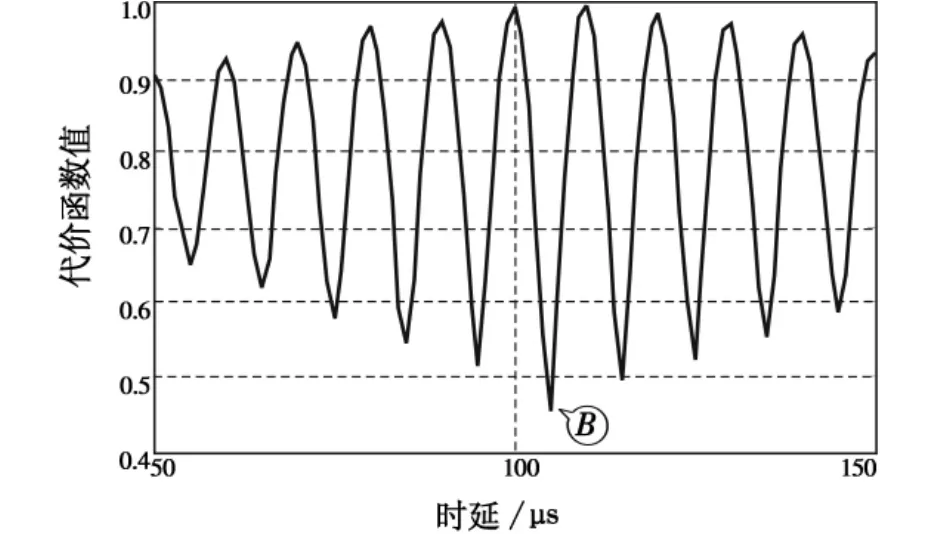
图5 幅度一定条件下对时延进行频域估计Fig.5 Estimating time delay with frequency-cost function under given amplitude
仿真2:验证时域估计幅度的有效性。
图6所示为不同天波时延估计值下在频域构造代价函数估计天波幅度的输出波形,图中C点所示为真实的幅度。可以看出,当时延估计准确时,最小值的位置与真实值接近;当时延估计不准确时,最小值的位置与真实值相差较远。图7所示为不同天波时延估计值下在时域构造代价函数估计天波幅度的输出波形,图中D点所示为真实的幅度。可以看出,虽然天波时延估计值发生变化,但是小值的位置与真实的时延位置相差不大。因此,在时域构造代价函数估计天波幅度受时延估计的影响小,估计精度高。仿真3:验证初始估计值对天波参数估计的影响。表1所示为初始估计值不同时天波参数的估计结果。
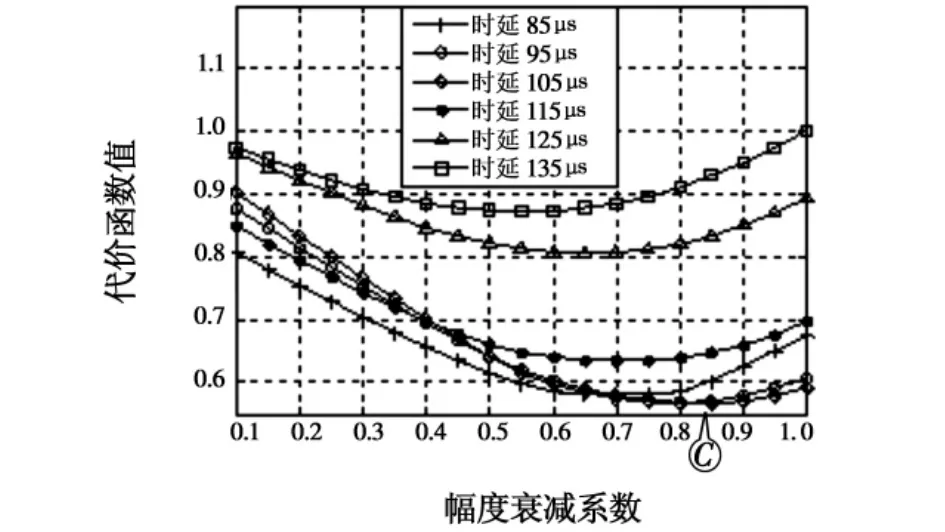
图6 在频域改变估计时延对幅度进行估计Fig.6 Estimating amplitude with frequency-cost function under various time delay

图7 在时域改变估计时延对幅度进行估计Fig.7 Estimating amplitude with time-cost function under various time delay
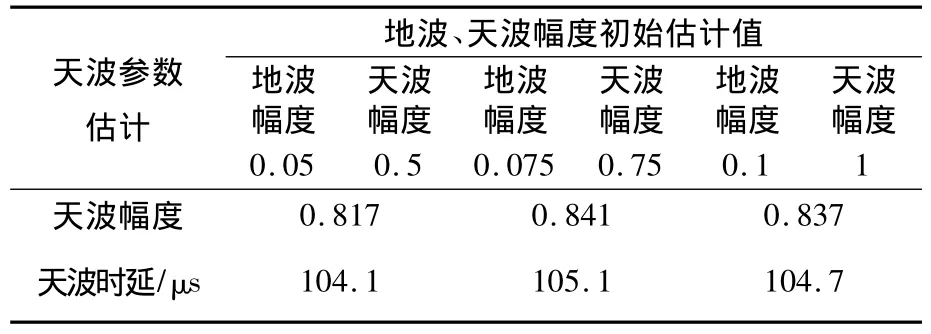
表1 不同初始估计值对天波参数估计的影响Table 1 The effect of different initial estimating values on parameter estimation of skywave
从表1中结果可以看出,通过迭代,尽管初始估计值估计不准确,对天波参数估计的结果影响不大。
仿真4:验证时频域估计的有效性。
只改变信噪比,其他仿真条件不变的情况下进行独立的20次MC仿真,每次迭代3次,仿真结果如表2所示。
从表2中的结果可以看出,相同的信噪比条件下,在时域对幅度进行估计的误差较小,在频域对时延进行估计的误差较小。因此采用时域和频域相结合的方法对时延和幅度进行估计的方法是可行的。并且将原有的在时域或者频域进行二维估计转化为分别在时域和频域进行一维估计,且估计精度要比单独在时域或频域进行二维估计的精度高。
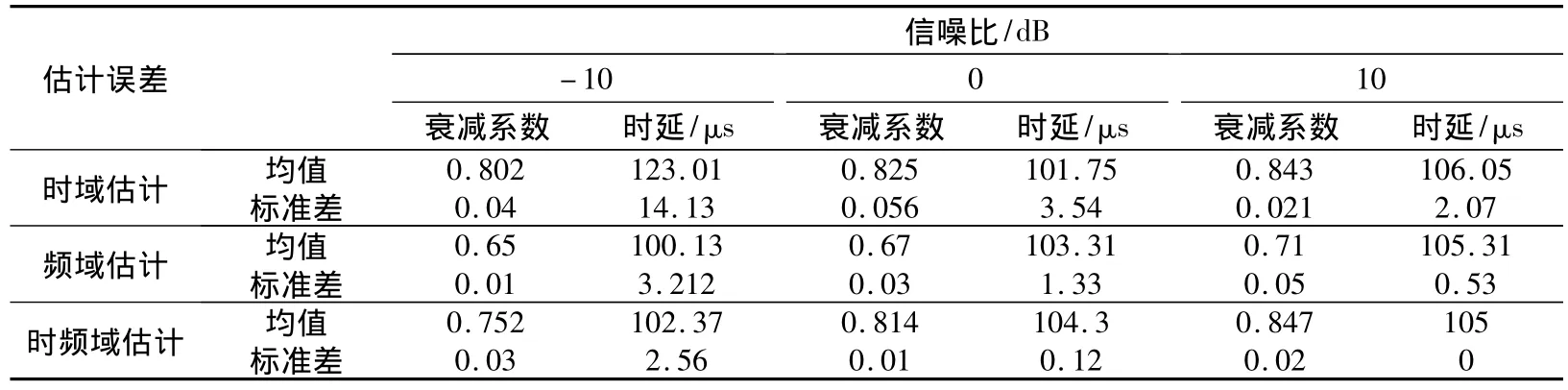
表2 不同信噪比下3种估计方法误差比较Table 2 Error comparison of three estimation methods under different SNRs
4 结束语
罗兰C导航定位系统的应用一直是有关部门关注的研究课题之一。但原有的固定基准点测量方法受噪声干扰大。本文利用罗兰C信号收发已知的特点,提出了通过时频域相结合构造代价函数寻优对天波信号时延和幅度进行估计。由于信号在时域和频域表现出的不同特性,对幅度和时延的估计呈现出不同的估计效果,进而在时、频域分别构造代价函数对幅度和频率进行分步估计,最后利用迭代提高估计精度。通过计算机仿真可以看出,此算法在较低的信噪比下依然有较高的估计精度。
[1]牛有田,田育蔗.罗兰C天波传播时延的间接法精确测量[J].电波科学学报,1994,9(9):36-44.
[2]吴德伟.现代航空导航系统[M].西安:空军工程大学电讯工程学院,2008.
[3]王明福,王仕成,罗大成,等.北斗/罗兰组合导航系统中伪距导航定位解算新算法研究[J].电光与控制,2006,13(4):16-18.
[4]柯宏发,杨保平,王建军,等.低信噪比信号检测识别技术[J].电光与控制,2002,9(4):45-49.
[5]喻胜,何丕雁.利用最小化代价函数方法实现多窗口谱分析[J].电子科技大学学报,1999,28(3):273-277.
[6]朱银兵,曹可劲,崔国恒,等.罗兰C信号数字处理方法分析[J].弹舰与制导学报,2006,28(6):222-225.
[7]杨迎春,杨新峰.高分辨率罗兰C天波延迟估计新技术[J].船舶电子工程,2006,26(1):133-136.
[8]马松涛,王化成,邓方林,等.罗兰C电波传播修正方法研究[J].战术导弹控制技术,2006(1):59-63.

