基于改进故障模型的CAN总线调度分析
吴 晨,叶星踪,许化龙
(1.第二炮兵工程学院,西安 710025;2.第二炮兵情报部,北京 100085)
0 引言
点对点互联模式在当前导弹控制系统互联网络中占据了绝对的主导地位,在这种体制下,弹上各节点之间交联复杂,模拟量、数字量、开关量等多种信号并存[1]。随着导弹数字化程度的深入,提出了弹载总线的概念。导弹控制系统的各单机部件都设计成一个独立的数字化部件,挂接在弹载总线上,形成一个开放的、信息高度共享的全分布式控制系统[2]。总线式体制下的导弹控制系统互联网络具有可扩展性强、可维护性高、可靠性高、体积小、重量轻等诸多优点,是导弹控制系统互联方式发展的必然趋势[3]。
CAN总线最初是由德国的BOSCH公司为汽车监测、控制系统设计的,采用多主工作方式、非破坏性仲裁技术、报文滤波通信、短帧结构等独特的设计,在汽车监控、工业自动化、智能建筑、医疗器械、船舶和航天通信等领域得到广泛的应用[4-5],是一种非常有发展前景的工业总线。导弹控制系统对通信任务的时间特性和安全特性十分敏感,但CAN总线由于采用了事件驱动型的通信协议,因此无法确定性地给出通信任务的完成时间估计,也就无法建立CAN总线的可靠调度算法。要建立基于CAN总线的导弹控制系统互联网络,就必须得到总线网络可靠的调度能力的准确分析。
Tindell和Burns给出了CAN总线的最坏情况下任务响应时间即WCRT(Worst Case Response Time)计算公式,建立了一种能确定性地评价总线调度能力的方法[6-8]。该方法已经被许多汽车制造商大力推广和应用,其有效的预测性使得CAN总线一改初期仅能在低负载率条件下稳定工作的状况而能在较高负载率下仍可靠稳定地工作。但是该方法的缺点在于其故障模型是建立在假定故障发生存在最小间隔的条件下,而在现实条件尤其是军事作战环境的恶劣条件中,故障的发生频率很可能高于此间隔而呈现强的随机性,因此该假设在强干扰环境中显得过于乐观。本文给出了一种更能准确模拟真实故障状况的基于泊松过程的故障模型,并基于此模型分析了基于CAN总线的导弹控制系统的消息调度策略。
1 CAN总线的WCRT分析
Tindell和Burns提出的WCRT分析方法,其思想就是计算出总线消息在最坏情况下的响应时间R(即从消息被触发开始到消息最终被接收节点成功接收完毕的时间开销),当该时间值小于消息的截止期限D,则认为该消息是可以调度的,否则该消息的传输就不具备绝对的可靠性和实时性。
Tindell和Burns的WCRT分析方法基于以下假设:
假设1 CAN总线上的任一个特定消息都以循环方式发送(比如,以某一种特定的间隔周期),并且此类消息都有相同的ID标识符和相同大小;
假设2 非周期性消息的发送存在一个最小发送间隔。则在最坏情况下,非周期性消息均以其最小发送间隔发送,此时可以作为周期性消息对待;
假设3 相邻故障的到达存在一个最小间隔Terror,且在任意时间间隔内,连串型故障有且仅有到1次。
将相同ID,相同周期(或者相同最小发送间隔),相同发送源的一类消息都称作一个任务。一个任务m可以用一个四元组来表示其属性:m=(Cm,Tm,Jm,Dm)。其中:Cm表示最坏情况下发送消息所需要的时间(不包括竞用总线的时间,但是包括发送ID字段的时间);如果该任务为周期性任务,Tm表示该任务的触发周期,如果为非周期性任务,Tm则表示其最小触发间隔;Jm表示最大触发抖动;Dm表示其截止期限。Rm≤min(Tm,Dm)是CAN总线的具备绝对实时性和可靠性的条件。
Rm由3个因素组成:即消息触发抖动延迟Jm,消息进行传输之前的排队等待延迟wm和消息在总线上的传输延迟Cm。排队延迟的原因来自于3个方面:故障导致的延迟Em,同时竞用总线的高优先级消息干扰延迟Im以及正在使用总线的低优先级消息阻塞延迟Bm。有:

式(2)中,
1)根据文献[9]有:
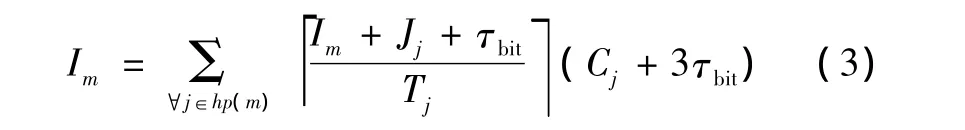
式中:τbit表示传输1 b的时间开销;Cj表示任务j的最坏情况下的传输延迟(3τbit是帧间隔的时间开销),用公式表示为
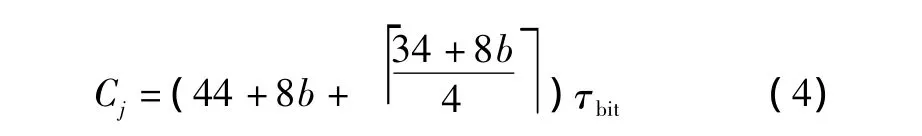
式(4)中,b为该任务的所有消息数据区的最大字节数。由文献[9]可知,式(3)利用迭代求解,即:

Im初始值可从0开始,迭代至满足结束。
2)在最坏情况下:
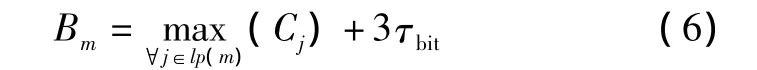
式(6)中,lp(m)表示优先级低于m的所有任务触发的所有消息的集合。
3)根据假设3,在时间t内,最坏情况下故障导致的时间延迟为
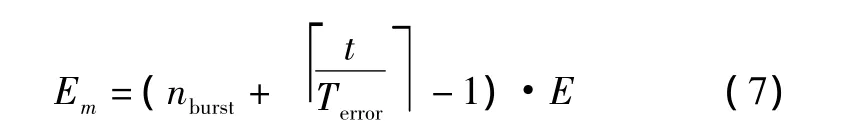
式中:nburst表示连串型故障的个数;E表示发现单个故障到恢复正常传输需要的最大时间开销。根据CAN总线协议,在最坏情况下(即故障发生在消息的最末一位):
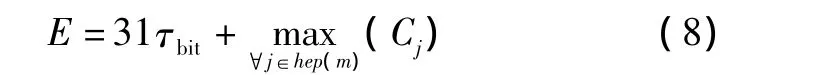
式(8)中,hep(m)表示优先级高于或等于m的所有任务触发的所有消息的集合。
将式(2)~式(8)代入式(1),运用迭代的方法解式(1),迭代至=或者 Rm≥min(Tm,Dm)时结束,其解满足Rm≤min(Tm,Dm)时为任务m最坏情况下的响应时间,否则该任务在该消息集下不可调度。
2 基于广义泊松过程的改进故障模型及其总线调度策略
现实环境中故障的类型可以分为单个故障和连串型故障。在普通干扰环境中,故障类型以单个故障为主;但是在强干扰环境下,比如持续扫描中的军事雷达的周边区域,或者高密度的电子线路环境,就会导致总线传输出现连续性的错误,称为连串型故障。故障持续的时间一般取决于总线载体通过强干扰区的时间。这两类故障的发生规律从统计学角度看都是随机的,且尤其是在强干扰环境下,故障在任何时间间隔内都有可能连续出现,Tindell提出的基于最小到达间隔的故障模型就显得过于乐观,因此会造成分析误差,使得消息实际响应时间大于WCRT。针对该问题,本文给出一种基于广义泊松过程的故障模型:即故障的到达服从泊松分布,而每次到达又以几何概率分布决定其故障持续发生个数。
2.1 模型描述
令X(t)为在时间区间[0,t]内发生的故障总个数,则有:
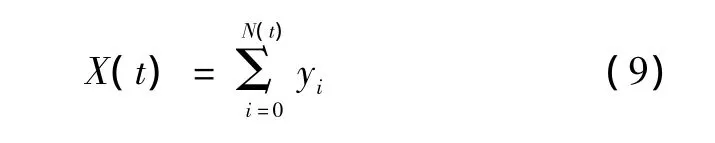
其中:
1)N(t)为在时间区间[0,t]内发生的故障次数,服从参数为λ的泊松分布,即:
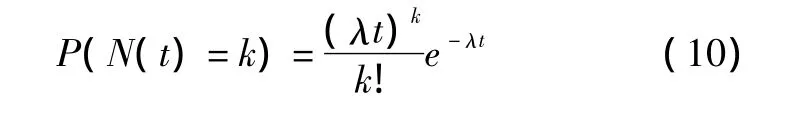
2)yi为在第i次故障中发生的故障个数,有:
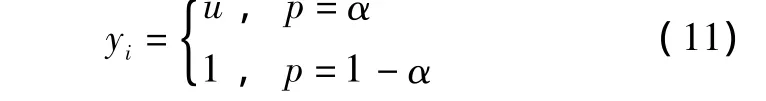
式中:u为随机变量,表示单次故障中故障可能发生个数的概率分布。
u的概率分布以及参数λ和α的取值都取决于具体CAN总线应用系统(如本文所讨论的基于CAN总线的导弹控制系统)的实际观察情况。目前流行的大多数CAN总线控制器都具备错误计数(如NEC控制器)和故障中断(如Philips控制器)的功能,这就为观察和记录系统的故障发生状况提供了技术基础[10]。
为了便于进一步讨论,本文选取几何分布作为随机变量u的概率分布,即有:
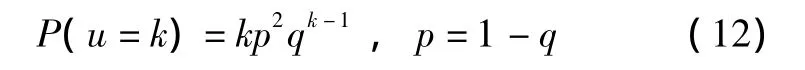
选取几何分布的原因是,几何分布能够满足P(u=0)=0,因为u=0是不允许发生的,且当k→∞时,几何分布的极限形式即是一种相对重要的排队分布,这使得问题易于求解。
有了u的分布以后,就可以求出单次故障发生个数yi的概率分布:
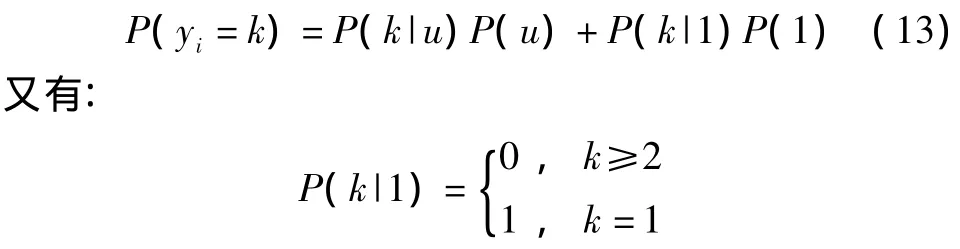
代入,则有:
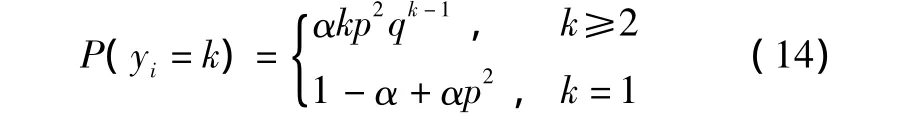
将式(14)代入式(9),可以得到X(t)的概率分布。
2.2 X(t)的算法实现
2.1 节中计算X(t)的方法的缺点在于计算量过大,使得计算时间过长,在本节给出一种更为可行的计算方法。根据X(t)的定义,有:
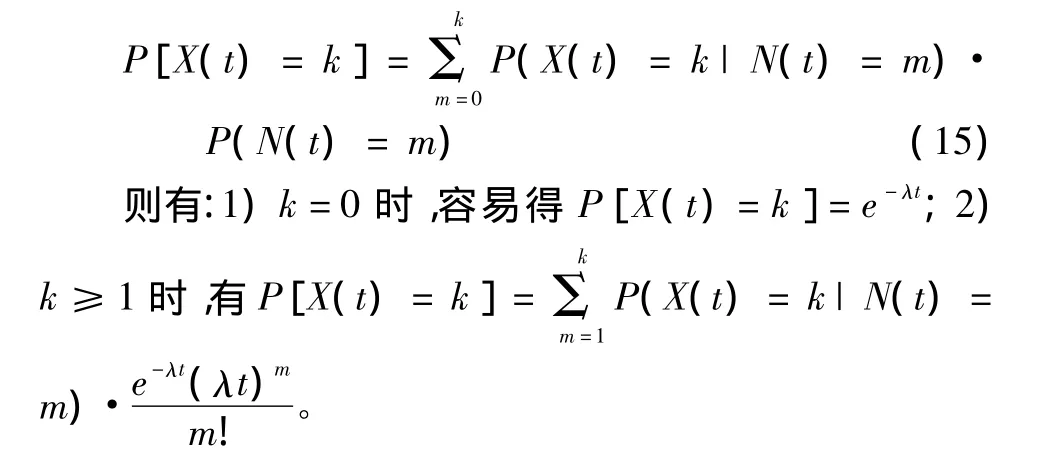
由于P(X(t)=k|N(t)=m)的意义就是m次故障中出现k个故障的概率,且又已知随机变量yi和N(t)是相互独立的变量,令,则有:
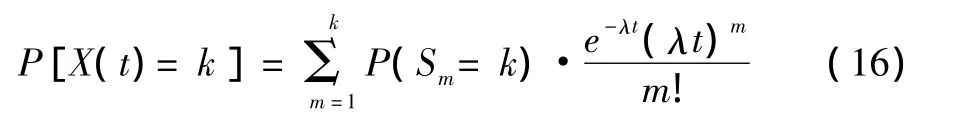
Sm是一个时间连续状态离散的马尔可夫链,则根据转移概率关系,有:
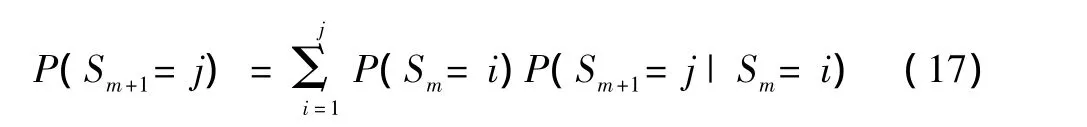
令ak=P(S1=k)=P(y1=k),应用切普曼-科尔莫葛洛夫方程,有:

上式的形式可使用递归进行求解,求解算法如下:
1)输入表示故障次数的参数m,以及表示故障个数的参数 k,调用函数 P_S(integer m,integer k)计算P(Sm=k)值;
2)初始化用来存储结果的变量result:result=0;
3)如果 m>k,则此事件不可能发生,故令result=0,并至 7);
4)如果m=1,则根据式(14)直接计算出ak的值,令result=ak,并至7);
5)如果 computed[m,k]=-1,说明该 P(Sm=k)并没有被计算过,则应用式(18)计算,并以新的参数m和k,至1)进行递归;
6)如果都不是以上情况,则说明该P(Sm=k)已经被计算出,则令 result=computed[m,k],并至7);
7)返回result给函数P_S(integer m,integer k),结束一次函数调用。
2.3 基于改进故障模型的CAN总线调度策略
由2.2节可以得到时间t内到达k个故障的概率。将(7)式改为下列形式,设n为故障个数:
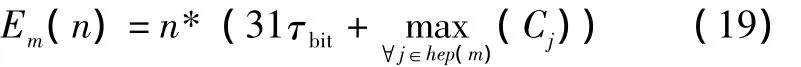
将上式代替式(7)代入(1)式进行迭代,则最后可以解出最坏情况下最大响应时间内可以容忍的最多故障数。对于任务m,在最坏情况下,传输任务失败的条件是在该任务的最大响应时间内到达的故障个数超过了其由上式推导出的该任务最大容忍故障个数,则任务m失败的概率可以由下式给出:
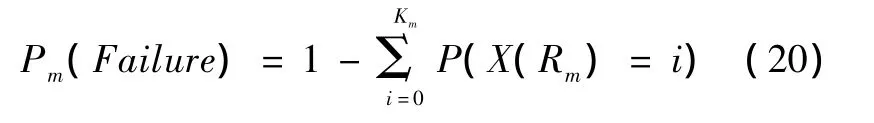
其中:Km表示任务m的最大容忍故障个数。
由上式可以计算出各个任务在最坏情况下的传输失败概率Pm。根据不同系统在实际使用中的不同需求,可以知道系统中各个数据传输任务的最大允许失败率 ρm。当 Pm>ρm时,则任务 m不可调度;Pm≤ρm时,则认为任务m可以调度。
3 基于CAN总线的导弹控制系统的调度分析
3.1 导弹控制系统消息传输任务分类
基于CAN总线的某型导弹控制系统的消息如表1所示。控制系统的消息传输任务由12种消息类型构成,分别来自8个节点。
3.2 消息可调度性分析
将式(19)代替式(7)代入式(1),由式(1)可计算表1中各消息对应的最坏情况下的响应时间Rm以及对应的最大可容忍故障个数Km,结果如表2所示。
取参数 α=0.1,p=0.04,λ=10和 30,则根据式(20),计算结果如图1所示。
从图1中可以发现,当λ的值越大,则系统中各消息的失败概率也越大。当λ=10时,对比ρm可知,各消息在最坏情况下的传输失败概率均能满足需求;当λ=30时,优先级为3的任务(压力传输器信号)的失败概率为0.03966,已经超出需求限制,为不可调度,其余任务仍满足需求限制。

表2 各任务对应的Km和RmTable 2 Kmand Rmresponding to each task
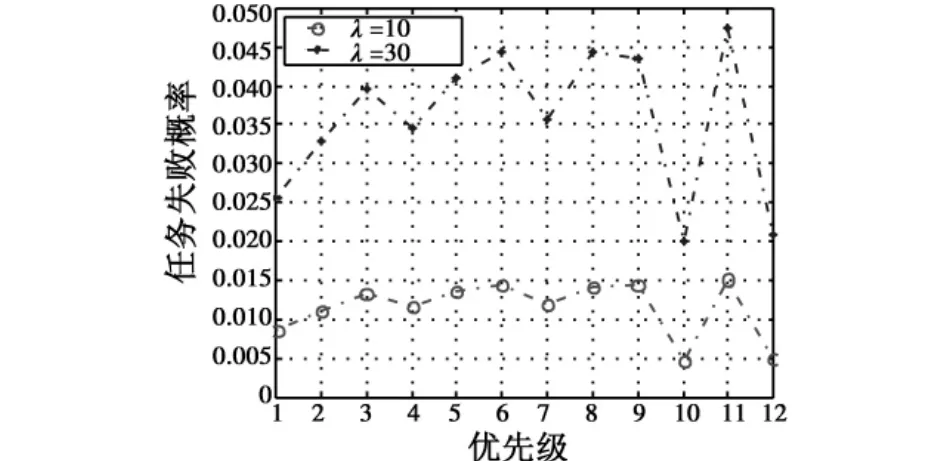
图1 导弹控制系统各消息传输任务失败概率Fig.1 The failure probability of each message transmission task of a missile networked control system
总体上,优先权较高的任务的传输失败概率较低。但是优先权显然并不是决定失败概率的唯一因素,周期长度是另外一个影响因素。优先级为11的任务,比它们相邻的任务拥有短得多的周期,其失败概率相对更高,即使它的优先级高于任务12。可见,周期越长,任务的失败概率也越低。
4 总结
Tindell和Burns给出的CAN总线的WCRT分析方法中的故障模型是基于最小间隔假设的。但是该假设不符合故障可能在小于最小间隔内连续发生的现实情况,尤其在强干扰环境中,该假设导致的误差将被放大,导致WCRT分析结果出现乐观偏差。为解决该问题,本文给出了一种基于泊松过程和几何概率分布结合的故障模型,并在此基础上建立了CAN总线消息的调度策略。最后作为示例,将该策略应用于基于CAN总线的导弹控制系统的消息调度分析中,显示了该策略的有效性,并分析了周期长度和优先级是对总线调度能力构成影响的因素。
[1]曾庆华,杜明波.总线型导弹控制系统状态监测与故障诊断技术[J].国防科技大学学报,2007,29(1):7-12.
[2]武翠琴,张向东,李艾华,等.导弹控制系统信息传输的网络化研究[J].弹箭与制导学报,2006,26(1):192-194.
[3]邹盛怀.航空火控系统中的高新技术[J].电光与控制,1997(4):1-10.
[4]叶强生,陈书明.CAN总线在汽车网络系统中的研究与应用[J].微计算机信息,2008(14):262-264.
[5]刘银春,何清华,贺继林.基于CAN总线的小型无人机飞控系统设计[J].微计算机信息,2008(28):23-25.
[6]TINDELL K.Fixed priority scheduling of hard real-timesystems[D].Department of Computer Science,University of York,1994.
[7]TINDELL K,BURNS A.Guaranteed message latencies for distributed safety critical hard real-time networks[R].Technical Report YCS 229,Department of Computer Science,University of York,May 1994.
[8]TINDELL K,BURNS A.WELLINGS A J.Calculating Controller Area Network(CAN)message response times[J].Control Engineering Practice,1995,3(8):1163-1169.
[9]AUDSLEY N C,BURNS A,RICHARDSON M,et al.Applying new scheduling theory to static priority pre-emptive scheduling[J].Real-Time Systems,1993,8(5):284-292.
[10]PELICAN P H.A new CAN controller supporting diagnosis and system optimization[C]//In 4th International CAN Conference,ICC'97,1997.
- 电光与控制的其它文章
- 用Linux实时系统设计飞机电子水平状态指示仪软件

