光纤信道自适应均衡器的仿真研究
王敬辉,刘剑飞,曾祥烨,王蒙军
(河北工业大学 信息工程学院,天津 300401)
对数字光纤系统而言,色散造成光脉冲的展宽,致使前后脉冲相互重叠,引起数字信号的码间串扰(ISI),造成误码率增加。光纤的损耗和色散是制约光纤通信系统无中继传输距离的2个主要因素。随着掺铒光纤放大器、色散补偿光纤以及色散补偿光纤光栅的出现,光纤中的损耗和色度色散已不是限制光纤传输性能的主要因素。但是无论怎样精心进行色散补偿和管理,残余色散、非线性和偏振模色散(PMD)等因素的影响总是存在的,诸如交叉连接、设备老化、环境变化等都可能导致残余色散超过系统设计的色散容限[1]。因此,为了减小色度色散[2]、模式色散[3]、PMD[4]等效应造成的 ISI,增加传输距离,降低信号发射功率,提高系统的健壮性,采用均衡方法。
1 均衡原理和仿真模型
均衡分为频率域上的均衡和时域上的均衡。前者是指在频率域上均衡信号各个频率分量的幅度和相位,使得传输通道在信号频谱范围内满足无失真传输条件。而后者是预测信号波形在临近的若干个判决时刻上的干扰,并设法消除。光纤通信系统的传输模型如图1所示,其中,{an}是待发送的数据序列。

图1 数字通信系统等效模型Fig.1 Equivalent model of digital communication system
系统总的传输特性为:
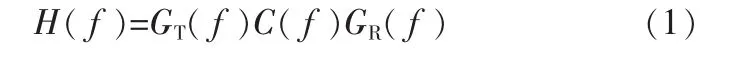
式中,GT(f)和 GR(f)分别是发送滤波器和接收滤波器的传输函数,C(f)是信道的传输特性。
为消除码间干扰,要求总的传输特性H(f)满足奈奎斯特准则,若已知发送滤波器传输特性GT(f)和信道传输特性C(f),则可容易设计接收滤波器特性GR(f),使系统总的传输特性满足奈奎斯特准则[5]。
在理想信道中,发送滤波器和接收滤波器联合设计成:所需采样瞬时t=nT,ISI为零,即:
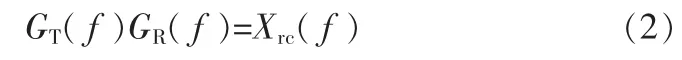
但是,一般情况下,信道传输特性不能准确获得,或者随时间变化。因此实际传输系统总的传输特性不能采用这种设计接收滤波器的方法,满足奈奎斯特准则要求。为了解决这个问题,在系统中另外插入一个均衡器,其传输特性用CE(f)表示,这样式(2)变为:
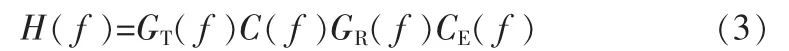
这时可以设计CE(f),使总的传输特性H(f)满足奈奎斯特准则,从而消除码间干扰。式(3)中,GT(f)为发送滤波器的频率响应,GR(f)为接收滤波器的频率响应,且GR(f)为GT(f)的匹配滤波器,Xrc(f)是升余弦频率响应特性,那么在采样时刻t=nT,ISI为零。然而,实际的光纤信道由于受噪声和光纤色散的影响,并不是理想的。
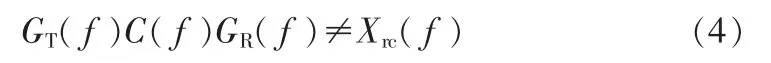
即产生信道失真,其中C(f)为实际光纤信道传输函数。为了消除光纤色散引起的码间干扰,在接收端加一个自适应均衡器 GE( f),并且使
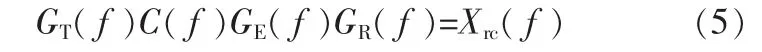
带均衡器的数字通信系统的等效模型如图2所示。由于只对抽样时刻上的抽样值感兴趣,故大大简化均衡器的设计。

图2 带均衡器的数字通信系统的等效模型Fig.2 Equivalent model of digital communication system with equalizer
图3为系统仿真模型,待发送数据经发送滤波器进入光纤信道,再经采样进入自适应均衡器,均衡器输出信号â(n)进入判决器,判决后输出 ã(n),将期望信号 d(n)和均衡器输出信号â(n)进行比较,得到误差信号,分别以LMS和RLS自适应算法为准则调整均衡器抽头系数,实现自适应的均衡。
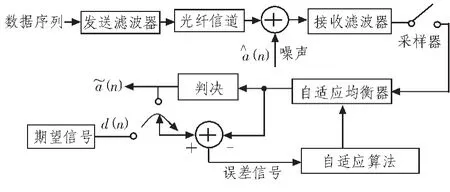
图3 基于判决反馈结构的仿真框图Fig.3 Structure diagram of simulation-based decision feedback
系统仿真参数为:光纤长度为100 km,光纤衰减常数为0.247 dB/km;光源增益0.98;比特率10 Gb/s的光传输系统;单极性非归零码型(NRZ);数据随机序列长度为5 000;信噪比为20 dB,每位采样数为10;发送成形滤波器为平方根滚降滤波器;3 dB带宽8 GHz;变换到电脉冲信号后送入判决反馈均衡器(DFE);采用基于最小均方误差 (LMS)算法和递归最小二乘(RLS)算法。
2 LMS算法和RLS算法
最小均方(LMS)算法由Widrow和Hoff引入,因其结构简单、稳定性好,一直是自适应滤波经典有效的算法之一,广泛应用于雷达、通信、声纳、系统辨识及信号处理等领域[6]。LMS算法一般采用递推的梯度(最陡下降)方法,用任意选择的可调节滤波器系数{h(k)}开始,然后将每一个新的输入样本{x(n)}输入到该自适应 FIR 滤波器,计算相应输出{y(n)},形成误差信号 e(n)=d(n)-y(n),并按方程
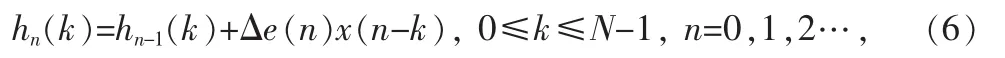
更新滤波器系数,这里△称作步长参数,x(n-k)是输入信号在时间n上位于滤波器第k个抽头上的样本;而e(n)x(n-k)是对第k个滤波器系数的一个梯度负值的近似估计,这就是为自适应的调节滤波器系数而使平方误差e2(n)之和ε达到最小的LMS递推算法。步长参数△控制了达到最优解的算法收敛速率。大的△步长值会导致大的步长调节,从而加速收敛;而小的△步长值会产生较慢的收敛,然而,如果△值取得太大,算法会变为不稳定。为了保证其稳定性,△必须在范围内。其中,N是自适应FIR滤波器的长度是输入信号的功率。
RLS算法采用最小平方逼近,相对于LMS算法采用的统计逼近,RLS算法能够得到更快的逼近。这是因为快速的收敛算法依赖于实际接收信号的时间平均误差表达式,而不是统计平均的误差表达式。
基于时间平均的最小平方误差:
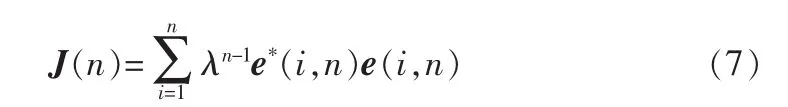
式中,λ是接近l,但小于1的加权因子。λ对各个时刻的误差具有一定的遗忘作用,则称作遗忘因子,其作用是对离n时刻越近的误差加比较大的权值,而对离n时刻越远的误差加比较小的权重。
e*(i,n)是e(i,n)的复共扼,且误差e(i,n)为
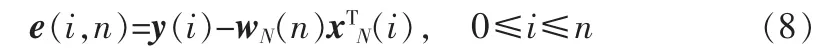
递归最小二乘算法可以总结如下:
l)初始化w(0)=k(0)=x(0)=0,R-I(0)=δINN,其中INN是N×N单位矩阵,N表示均衡器抽头延时线上延时级数,且δ是一个数值很大的正常数。
2)按照下列方程进行递归计算:
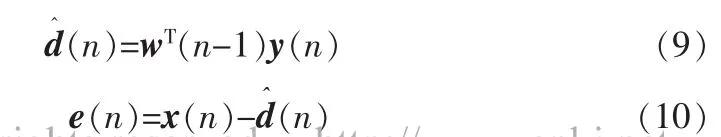
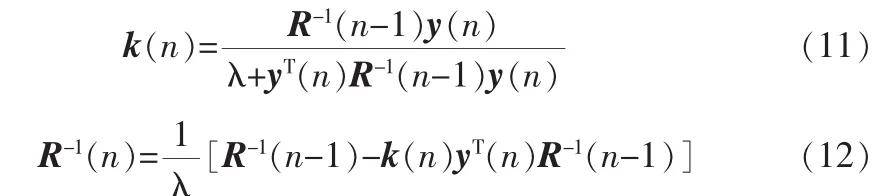
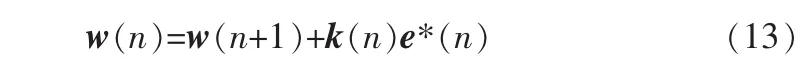
3 仿真结果
仿真结果如图4所示。
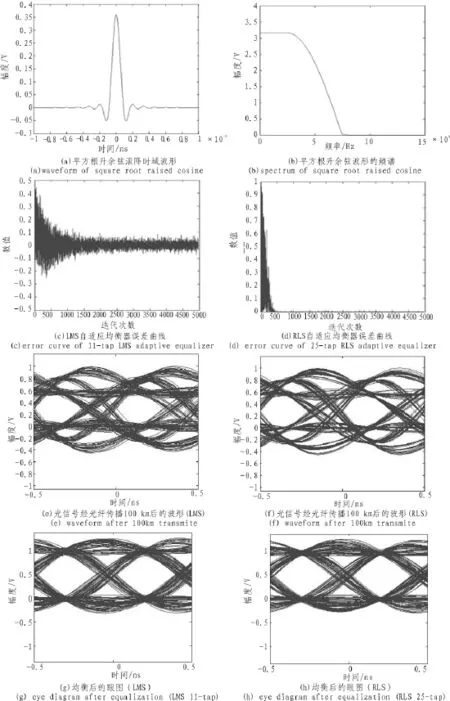
图4 11抽头LMS算法均衡器和25抽头RLS算法均衡器输出结果Fig.4 Program execution output results of 11-tap LMS algorithm equalizer and 25-tap RLS algorithm equalizer
信道中加入指定信噪比的零均值高斯白噪声,LMS算法的均衡器抽头数为11,调整步长为0.01,RLS算法均衡器抽头数为25,遗忘因子为 0.98,调整步长为0.01。其中图4(a)图是脉冲信号经发送成形滤波器后输出的时域波形,图4(b)是图 4(a)信号的频谱图。 从图 4(c)和(d)可以看出 11 抽头LMS自适应均衡器的误差信号要大于25抽头RLS自适应均衡器的误差信号,RLS算法自适应均衡器性能更优。从图4(e)和(f)可以看出光纤色散导致码间干扰的产生。从图 4(g)和(h)可以看出LMS自适应均衡器和RLS自适应均衡器均能够改善信号输出,有效消除码间干扰,25抽头RLS自适应均衡器比11抽头LMS自适应均衡器的均衡性能要好,收敛速度更快,但是以提高计算量为代价的。
4 结 论
LMS算法和RLS算法都比较简单、运算高效性,在各种条件下具有良好性能。对于高速光纤通信系统LMS算法和RLS算法同样能很好的对光纤信道进行均衡,有效消除光纤色散和PMD引起的码间干扰。但RLS算法稍微复杂,但收敛速度更快,性能更好。所以,基于这两种算法的自适应均衡器都能很好满足对均衡速度要求较高的光纤通信系统。
[1]顾畹仪,闻和.WDM超长距离光传输技术[M].北京:北京邮电大学出版社,2006.
[2]Buchali F, Bulow H, Baumert W,et al.Reduction of the chromaticdispersion penaltyat10Gbit/sbyintegrated electronic equalizers[C]∥in Techn.Dig.OFC'00 ,Baltimore,Mar.7-10,ThS1 2000,268-270.
[3]Ingham J D, Penty R V, White I H,et al.Electronic equalization for length extension of×2 to ×3 in 10Gbit/s multimode-fiber data communication links[J].Electron.Lett..,2004,40(22):1473-1439.
[4]Bulow H, Buchali F, Baumert W,et al.PMD mitigation at 10Gbit/s using liner and nonlinear integrated electronic equalizer circuits[J].Electron.Lett.,2000,36(2):163-164.
[5]樊昌信,张甫翊,徐炳祥,等.通信原理 [M].5版.北京:国防工业出版社,2001.
[6]张贤达.现代信号处理 [M].北京:清华大学出版社,2002.

