基于扩孔理论的混凝土钢筋锈胀开裂分析

唐孟雄，陈晓斌,

(1. 广州市建筑科学研究院，广东 广州，510440；2. 中南大学 土木建筑学院，湖南 长沙，410075)

钢筋锈蚀膨胀是钢筋混凝土结构使用寿命预测的核心问题，许多学者对此进行了研究，如：Bazant[1]对锈蚀产物胀裂保护层开裂过程进行了弹性分析；Andrade等[2]采用分布裂缝模型，编制了锈胀损伤过程的有限元分析程序，分析了钢筋锈胀过程；屈文俊等[3]给出了一般边和角区胀裂时钢筋锈蚀量的计算公式；Liu等[4]考虑锈蚀产物向钢筋周围混凝土孔隙的扩散，研究了钢筋锈蚀量与表面混凝土开裂之间的关系；Perterson[5]应用弹性力学给出了单位长度半径为 r的圆柱体未开裂部分的环向应力公式；Morinaga[6]提出的锈胀开裂压力公式与混凝土抗拉强度、混凝土保护层厚度、钢筋直径有关；金伟良[7]应用弹性力学理论提出了由钢筋均匀锈蚀导致的保护层胀裂时刻钢筋锈胀力计算公式；赵羽习等[8]建立非线性有限元模型，对混凝土构件受钢筋锈胀力作用的情况进行模拟，并在此基础上提出了基于有限元数值分析的混凝土锈胀时刻钢筋锈蚀率计算方法；王海龙[9]考虑了混凝土和钢筋的实际变形情况以及混凝土界面中的原始裂纹与缺陷，得到混凝土保护层开裂时钢筋的膨胀力和均匀锈蚀率的理论预测模型；李海波等[10]用实验方法研究了混凝土开裂时的钢筋锈蚀率与钢筋直径、混凝土等级与保护层厚度之间的定量关系，通过有限元计算得到了锈胀开裂力。在此，本文作者采用圆孔扩张理论对混凝土钢筋锈胀问题进行分析，求解不同钢筋锈蚀量对应的混凝土拉应力及塑性区半径公式，推导与保护层开裂时刻对应的临界钢筋锈蚀率 ρ(t)模型，并对模型主要影响因素进行理论分析，以便为进一步研究碳化或者氯离子侵蚀的钢筋锈胀开裂寿命预测提供理论基础。

1 钢筋锈胀扩孔模型

1.1 基本假设

在对混凝土钢筋锈胀进行分析前，进行如下假设：

(1) 钢筋混凝土是各向同性体，钢筋的锈蚀体积呈匀速线性规律膨胀，锈胀力分布均匀。混凝土为理想塑性材料，满足莫尔-库仑屈服准则。

(2) 需要分析的钢筋混凝土几何形状、约束边界、所加荷载分布均对称于钢筋中轴线，简化为平面轴对称问题。

(3) 在均匀分布锈胀压力作用下，钢筋周围的圆筒形混凝土区从内向外由塑性区和弹性区组成。其中，塑性区随着压力的增加而不断扩大，混凝土锈胀开裂模型见图1，其中：r为圆孔半径；σp为圆孔塑性区径向压力；σr为径向正应力；σθ为环向正应力；up为塑性区径向小变形(弹性区径向应力作用下)；Rp为锈胀过程中塑性区半径；Pu为相应的最终内压力，设钢筋锈蚀前半径和混凝土开裂前半径分别为R0和Ru，即相当于圆孔的初始半径R0和扩张后的终半径Ru。在半径Rp以外，混凝土弹性区处于弹性平衡状态。

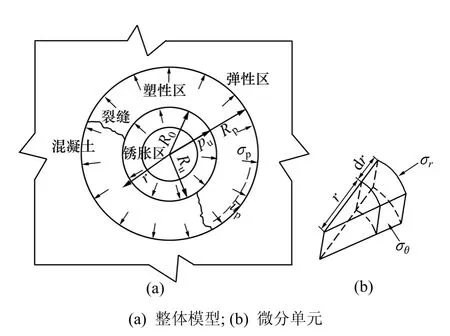
图1 混凝土锈胀开裂模型Fig.1 Rebar corrosion expansion cover cracking model

(4) 钢筋生锈膨胀均匀，锈蚀钢筋变形简化成图2所示。

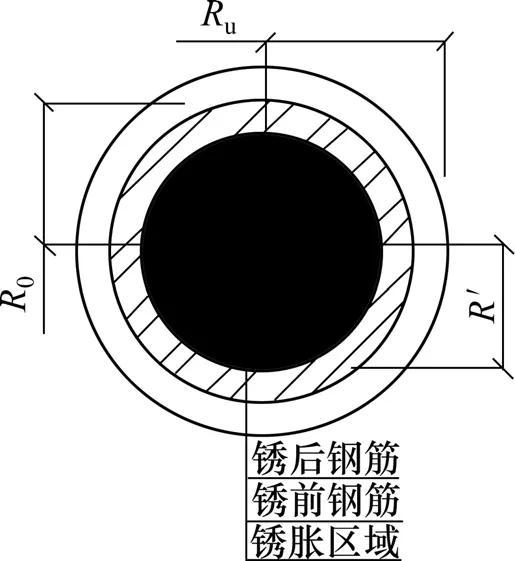
图2 钢筋锈胀变形Fig.2 Rebar’s deformation during corrosion expansion

依据钢筋变形模型，有[11]：

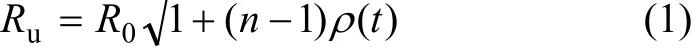
尚未锈蚀的钢筋半径为：

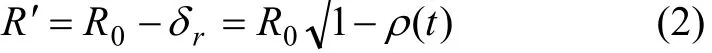
式中：δr为钢筋锈胀后的径向位移；n为铁锈体积膨胀倍数，一般取n=2～4[12]；ρ(t)为钢筋锈蚀率，它与环境因素相关，由试验确定。

1.2 理论推导

对图1所示锈胀开裂概化模型，采用极坐标系进行分析。由平面应力关系，得θτr=0，其中，τrθ为圆孔对应半径剪应力。采用莫尔-库仑准则为混凝土塑性区边界屈服准则，即

式中：E为混凝土弹性模量；µ为混凝土泊松比；φ混凝土材料内摩擦角；c为混凝土黏聚力。

由扩孔理论解得弹性区域内任意点处应力和位移解析式，其中应力为[13]：

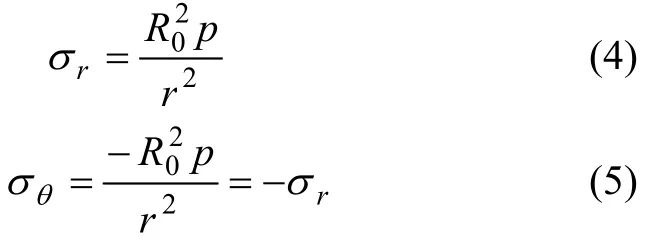
r＞Rp时，任意点的位移为：

对于塑性屈服边界，有如下微分方程：

式(7)为变量可分离微分方程。结合边界条件r=Ru，σr=pu，方程(7)的解为：

对于塑性区边缘，r=Rp，式(8)变为：

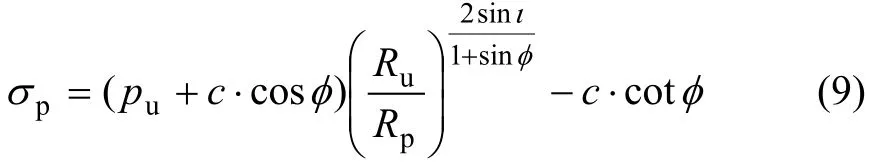
式中：φ，c和Ru为已知量。混凝土总应变为弹性应变与塑性区应变之和，依据变形协调条件，有如下关系：

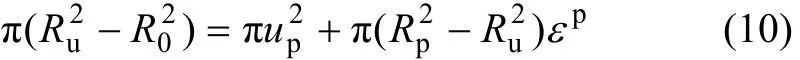
式中：εp为塑性区平均应变。整理式(10)，并等效替换高阶小量得：

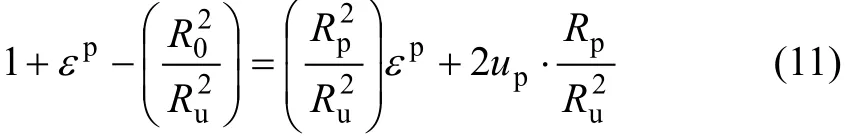
对于弹性与塑性分界点，由连续条件得：

将式(9)代入式(12)得：

将式(13)代入式(11)得：

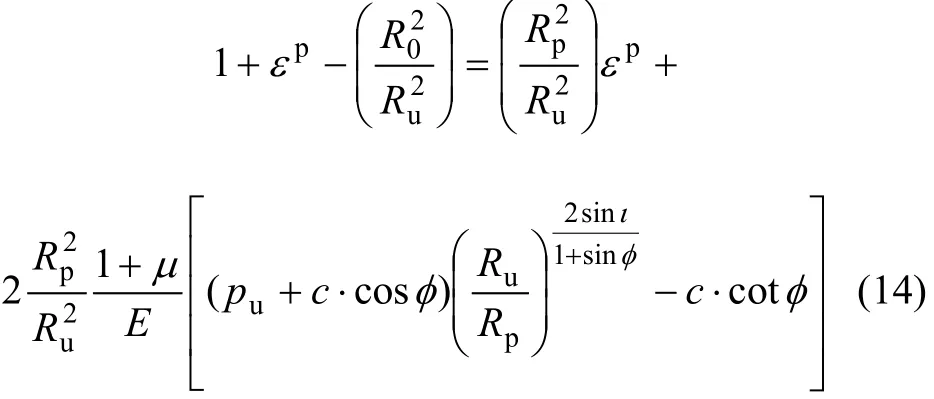
在屈服边界有 r=Ru，σr=σp=-σθ，依据莫尔-库仑屈服准则，可以求得：

将式(15)代入式(9)得：

联合式(14)和式(16)方程组，解方程组可得塑性区半径为：

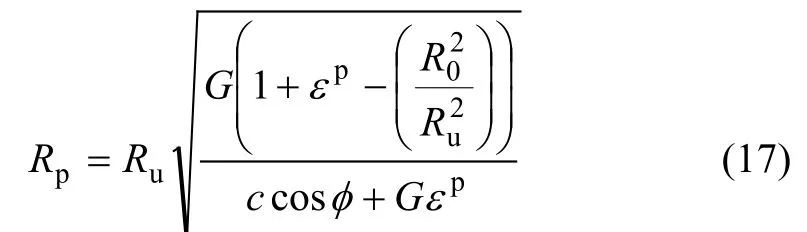
其中：G为剪切模量。

终压力pu为：

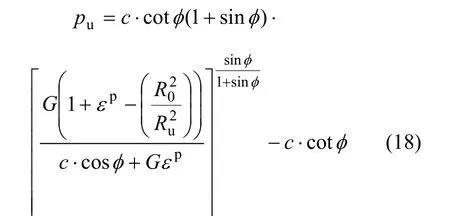
将式(17)和(18)代入式(9)，得到 r=Rp塑性区边界混凝土应力：

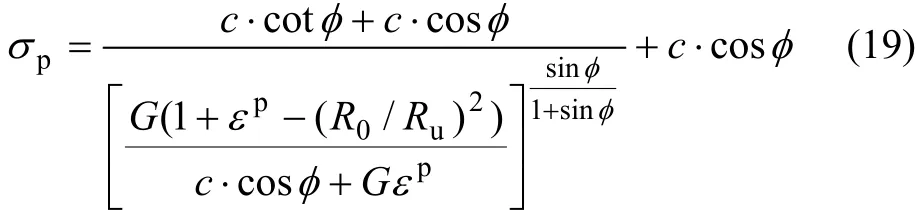
2 混凝土锈胀寿命准则

2.1 锈胀寿命准则

国内外许多学者针对钢筋锈蚀造成的混凝土开裂寿命进行了预测，提出了不同的寿命准则。Tuutti[14]提出了两阶段预测模型；Mehta[15]对该模型进行了改进；Morinaga[16]以氯离子引起钢筋锈蚀以致混凝土出现裂缝作为寿命准则；Funahashi[17]提出以钢筋开始锈蚀作为寿命终结的标志；刘西拉等[18]以纵向开裂截面损失率达 5%作为寿命终点；牛荻涛等[19]认为重要建筑物的寿命应采用锈胀开裂寿命准则进行评估。在锈胀开裂寿命预测方面，目前缺少统一标准。

2.2 基于扩孔的准则

假定锈胀过程如图3所示。浇固在混凝土中钢筋生锈膨胀，当塑性区半径穿过钢筋保护层厚度hc时，混凝土锈胀开裂，结构严重劣化，此刻为锈胀开裂寿命，对应着临界钢筋锈蚀率。

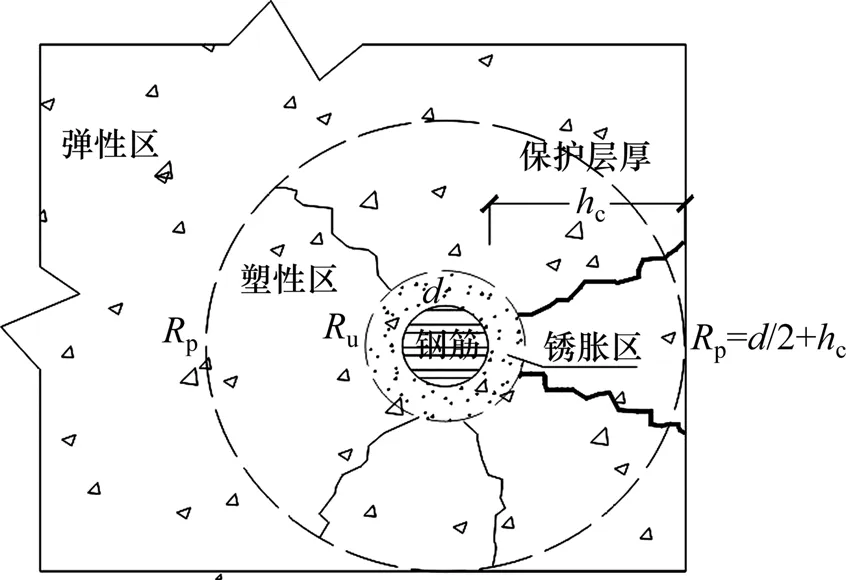
图3 混凝土锈胀开裂过程Fig.3 Cover cracking due to rebar corrosion expansion

基于扩孔理论的混凝土锈胀寿命准则为：

已知混凝土强度等级(E，u，c和φ)、混凝土钢筋保护层厚度为hc、钢筋直径为d，有：

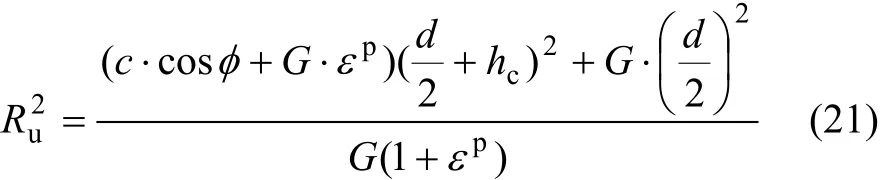
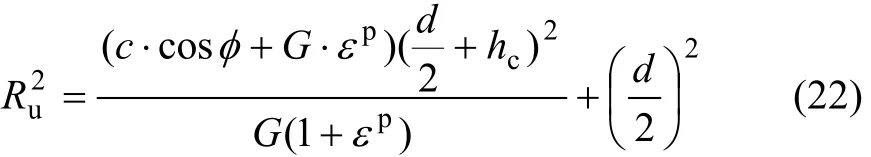
定义m为相对保护层厚度：

将式(1)及(23)代入式(22)并化简得：

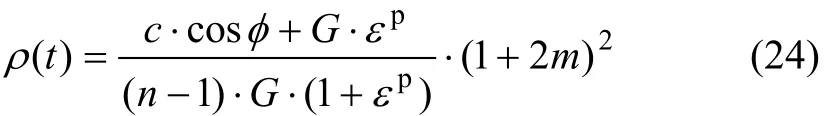
根据得到的混凝土保护层开裂时临界钢筋锈蚀率，选择合理的钢筋锈蚀速度模型，即可求得锈胀开裂寿命t。

3 寿命预测模型分析

3.1 相对保护层厚度m的影响

为了分析模型中相对保护层厚度m的影响，采取算例进行试算分析，算例参数见表1。

表1 相对保护层厚度影响算例参数Table 1 Case analysis parameters of relative covering depth effects

钢筋相对保护层厚度m分别取0.5，1.0，1.5，2.0，2.5，3.0和4.0，将参数代入式(24)，经计算得到临界钢筋锈蚀率随着相对保护层厚度变化曲线，如图 4所示。

图4 相对保护层厚度m与临界锈蚀率关系Fig.4 Relationship between relative cover depth and limit rebar corrosion ratio

从图4可知：随着相对厚度m增加，锈胀开裂临界锈蚀率快速增加；当m＝1.0时，hc＝20 mm，临界锈蚀率为1.01%；当m＝2.5时，hc＝50 mm，临界锈蚀率为4.05%。相对保护层厚度m与临界锈蚀率关系说明增加混凝土保护层厚度对耐久性设计具有重要意义，同时也说明当相对厚度满足一定条件时，混凝土保护层才能锈胀开裂。这说明在很大的保护层下可能不会出现锈胀开裂现象，此时锈胀开裂寿命准则失效，需要改用其他方法评价混凝土结构寿命。

3.2 铁锈膨胀率n的影响

为了分析模型中铁锈膨胀率n的影响，采取不同n的算例进行试算，算例参数见表2。

表2 铁锈膨胀率影响算例参数Table 2 Case analysis parameters of rust expansion rate effects

铁锈膨胀率n分别取0.5，1.0，1.5，2.0，2.5，3.0，3.5和4.0。当m=2时，铁锈膨胀率n与钢筋临界锈蚀率关系见图5。

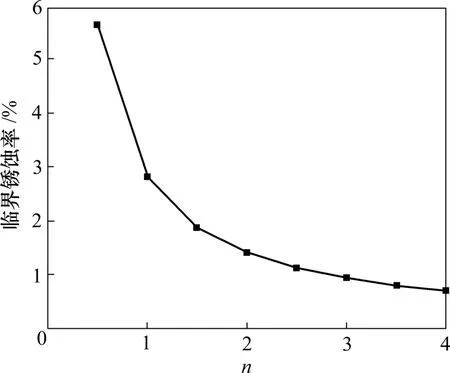
图5 m=2时铁锈膨胀率n与临界锈蚀率关系Fig.5 Relationship between rust expansion rate n and rebar corrosion rate when m=2

从图5可知：随着铁锈膨胀率n的增加，临界锈蚀率呈几何级数快速下降，铁锈膨胀率n对混凝土结构锈胀开裂的影响非常大。这说明在实际工程应用中，应该尽量避免铁锈生成结晶物的环境，以减小 n，确保混凝土结构的耐久性。

3.3 混凝土强度等级的影响

此算例分析不考虑混凝土强度等级增加对抗渗性能增加的影响，单纯从力学机理进行分析。混凝土等级决定了莫尔-库仑材料模型中的参数E，u，c和φ，这些参数综合影响钢筋临界锈蚀率。其中，u和φ变化幅度较小，为了简化分析，u和φ取定值。混凝土强度等级影响算例参数见表3。

由于u和φ取定值，因此，式(24)可以化简为：

式(25)说明临界锈蚀率只与比值c/E相关，随着c/E增大而增大。在此，混凝土粘聚力取混凝土抗拉强度tσ，不同强度等级混凝土参数见表4。

表3 混凝土强度等级影响算例参数Table 3 Case analysis parameters of different strength grade of concrete

表4 不同强度等级混凝土参数[20]Table 4 Parameters of different strength grades of concretes[20]

将表 4中的参数代入式(25)经等效换算后，得到m=2时混凝土强度等级与临界钢筋锈蚀率关系，如图6所示。

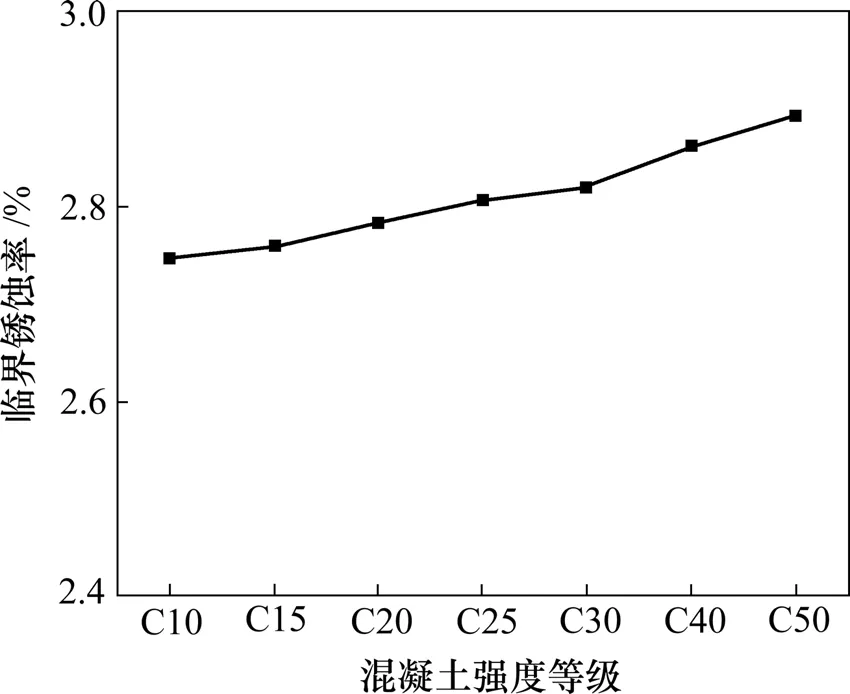
图6 m=2时混凝土强度等级与锈蚀率关系Fig.6 Relationship between concrete strength grade and rebar corrosion rate when m=2

从图6可知：在不考虑混凝土强度等级增加对抗渗性能提高的影响时，随着混凝土强度等级增加，扩孔理论计算得到的混凝土结构锈胀开裂临界锈蚀率缓慢增加；当m=2.0时，C10混凝土对应的临界锈蚀率为 2.71%，C30混凝土对应的临界锈蚀率为 2.82%。这说明在混凝土结构耐久性设计中，单纯提高混凝土强度等级的方法增加结构耐久性并不适宜。

4 结论

(1) 采用圆孔扩张理论求解了钢筋锈胀混凝土应力及塑性区半径公式，并建立了基于圆孔扩张理论的混凝土锈胀开裂寿命准则及寿命预测模型。

(2) 混凝土锈胀开裂寿命t与混凝土强度等级、相对保护层厚度和铁锈膨胀率有直接关系。相对保护层厚度增加，锈胀开裂临界锈蚀率快速增加，铁锈膨胀率增大，临界锈蚀率快速下降，混凝土强度等级增大，临界锈蚀率增加缓慢。

(3) 在增强耐久性措施方面，增加混凝土保护层厚度效果显著，单纯增加混凝土强度等级不适宜，钢筋混凝土结构应该避免大量铁锈结晶物生成环境。

(4) 预测模型为进一步研究单独考虑碳化或者氯离子侵蚀下的钢筋锈胀开裂寿命预测提供了理论依据。

[1] Bazant Z P. Crack-band theory for fracture of concrete[J].Material and Structures, 1983, 16(6): 155-177.

[2] Andrade C. Cover cracking as a function of bar corrosion. PartⅠ: Experimental test[J]. Material and Structures, 1993, 26(5):453-464.

[3] 屈文俊, 张誉. 侵蚀性环境下混凝土结构耐久寿命预测方法探讨[J]. 工业建筑, 1999, 29(4): 40-44.QU Wen-jun, ZHANG Yu. Discussion on the predicting method about durability life of concrete structure under erosion environment condition[J]. Industrial Construction, 1999, 29(4):40-44.

[4] Liu Y, Weyers R E. Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures[J]. ACI Material Journal, 1998, 95(6): 675-681.

[5] Peterson J E. A time to cracking model for critically contaminated reinforced concrete structures[D]. Virginia:Virginia Polytechnic Institute and State University, 1993: 25.

[6] Morinaga S. Prediction of service lives of reinforced concrete buildings based on the rate of corrosion of reinforcing steel[C]//Special report of the Institute of Technology. Tokyo:Shimizu Corporation, 1989: 125-130.

[7] 金伟良. 钢筋混凝土构件的均匀钢筋锈胀力的机理研究[J].水利学报, 2001, 7(7): 57-63.JIN Wei-liang. The mechanism of corroded expansion force of reinforced concrete members[J]. Journal of Hydraulic Engineering, 2001, 7(7): 57-63.

[8] 赵羽习, 金伟良. 混凝土锈胀时刻钢筋锈蚀率的数值分析方法[J]. 浙江大学学报: 工学版, 2008, 42(6): 1080-1084.ZHAO Yu-xi, JIN Wei-liang. Numerical-based method for calculating reinforcement corrosion at concrete cover cracking due to corrosion[J]. Zhejiang University: Engineering Science,2008, 42(6): 1080-1084.

[9] 王海龙. 冻融环境下钢纤维对轻骨料混凝土力学性能的影响[J]. 混凝土, 2006, 226(8): 65-68.WANG Hai-long. Effect of steel fiber on mechanical properties of lightweight aggregate concrete to freeze-thaw environment[J].Concrete, 2006, 226(8): 65-68.

[10] 李海波, 鄢飞, 赵羽习, 等. 钢筋混凝土结构开裂时刻的钢筋锈胀力模型[J]. 浙江大学学报: 工学版, 2000, 34(4): 415-422.LI Hai-bo, YAN Fei, ZHAO Yu-xi, et al. Model of corroded expansion force at cracking on reinforced concrete structure[J].Zhejiang University: Engineering Science, 2000, 34(4):415-422.

[11] 惠云玲, 林志伸, 李荣. 锈蚀钢筋性能试验研究分析[J]. 工业建筑, 1997, 26(6): 10-13.HUI Yun-lin, LIN Zhi-shen, LI Rong. Experimental study and analysis on the property of corroded rebar[J]. Industrial Construction, 1997, 26(6): 10-13.

[12] 金伟良. 钢筋混凝土构件的均匀钢筋锈胀力及其影响因素[J].工业建筑, 2001, 31(5): 6-8.JIN Wei-liang. Corroded expansion force of reinforced concrete members and its influence factors[J]. Industrial Construction,2001, 31(5): 6-8.

[13] 徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社,1983: 32-34.XU Zhi-lun. Elastic theory[M]. Beijing: Higher Education Press,1983: 32-34.

[14] Tuutti K. Effect of cement type and different additions on service life[J]. Concrete, 1993, 25(2): 1285-1296.

[15] Mehta P K. Concrete durability fifty year’s progress[C]//Proceeding of 2nd International Conference on Concrete Durability. Montreal: ACI, 1991: 1-33.

[16] Morinaga F J. Cover cracking as a function of bar corrosion. PartⅡ: Numerical model[J]. Materials and Structures, 1993, 26(9):932-948.

[17] Funahashi M. Predicting corrosion free service life of a concrete structure in a chloride environment[J]. ACI Material Journal,1990, 87(2): 581-587.

[18] 刘西拉, 苗澍柯. 混凝土结构中的钢筋腐蚀及其耐久性计算[J]. 土木工程学报, 1990, 23(4): 69-78.LIU Xi-la, MIAO Shu-ke. Steel corrosion and the durability calculation of reinforced concrete structures[J]. China Civil Engineering Journal, 1990, 23(4): 69-78.

[19] 牛荻涛, 王庆霖, 王林科. 锈蚀开裂前混凝土中钢筋锈蚀量的预测模型[J]. 工业建筑, 1996, 26(4): 8-10.NIU Di-tao, WANG Qing-lin, WANG Lin-ke. Predeterminate model of steel corrosion extent in reinforced concrete structures before producing corrosion crack[J]. Industrial Construction,1996, 26(4): 8-10.

[20] 宋玉普, 王清湘. 钢筋混凝土结构[M]. 北京: 机械工业出版社, 2004: 54.SONG Yu-pu, WANG Qing-xiang. Reinforce concrete structure[M]. Beijing: China Machine Press, 2004: 54.