梨木虱若虫空间分布型及抽样技术研究
王彩敏
梨木虱若虫空间分布型及抽样技术研究
王彩敏
(郑州市世纪游乐园管理处,河南 450000)
通过各聚集度指标的计算及Iwao的平均拥挤度和平均数的回归分析法和Taylor的幂的法则测定了梨木虱若虫的空间分布型,并进一步探讨了不同抽样方法的准确度及空间分布型在序贯抽样中的应用。
梨木虱;空间分布型;抽样技术
近年来,梨木虱(Psylla pyrisuga Forster)在郑州郊区梨园普遍发生,造成危害严重。为了有效地对梨木虱进行预测预报和正确指导防治,首先对梨木虱若虫在梨树上的分布型及抽样技术进行了调查研究,现将研究初报如下:
1 空间分布型的测定
1.1 调查方法
2008年4-5月我们在梨园对梨木虱若虫进行调查。根据梨木虱发生程度及梨园结构我们共划分了6块调查样地,每块20株梨树,在树冠上、中、下3层分别按东、南、西、北、中5个方位采叶,每个方位采10片叶子,每棵树共抽取150片叶子,检查记录每1片叶上 (包括叶柄、叶基部) 梨木虱若虫数,并分别记载统计。
1.2 分布型的判断分析方法
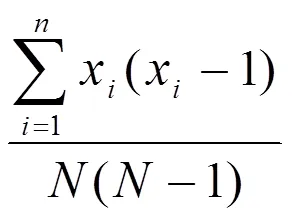
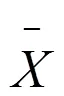
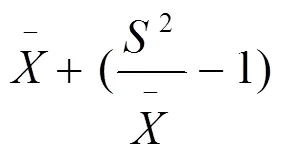

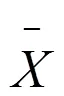
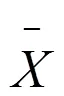
1.3 结果分析
1.3.1各聚集指标值计算
根据6组调查统计资料,分别按以上公式计算的各聚集度指标值如表1。
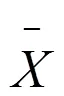
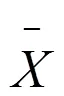
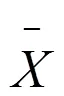
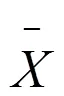
由上式可明显看出, α=1.38>0说明在调查虫口密度范围内,梨木虱卵分布较集中,若虫相互间无排斥性,存在着个体群。 β=4.28>1 说明其分布为聚集型分布。(1,2)
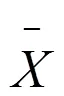
说明梨木虱若虫种群在调查密度范围内均是聚集的,且具有密度依赖性(2)。
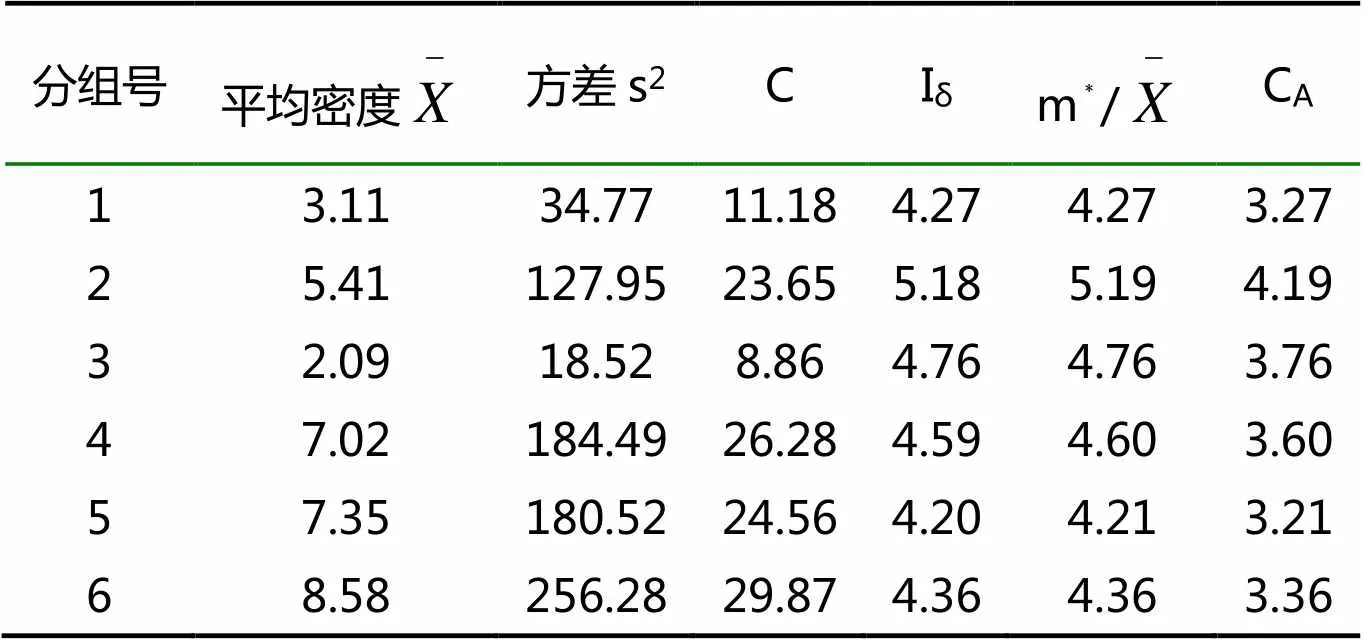
表1 梨木虱各聚集指标值(若虫)
2 梨木虱若虫空间分布型在抽样技术中的应用
2.1 不同抽样方法准确程度比较
结合以上分布型的调查,我们取其中相邻的2个野外调查小区共60株树的调查数据,按林间梨树行、列排列顺序分别填入对应的方格纸中,然后,依次按平行线法、五点式取样法、双对角线取样法、 Z字形法,四种取样方式在方格纸上定株对应取样,每种方式取样15株,共150个叶丛枝,分别统计各种取样方法的平均虫口密度,并以全林(60株)为对照计算平均数差值和变异系数(表2)
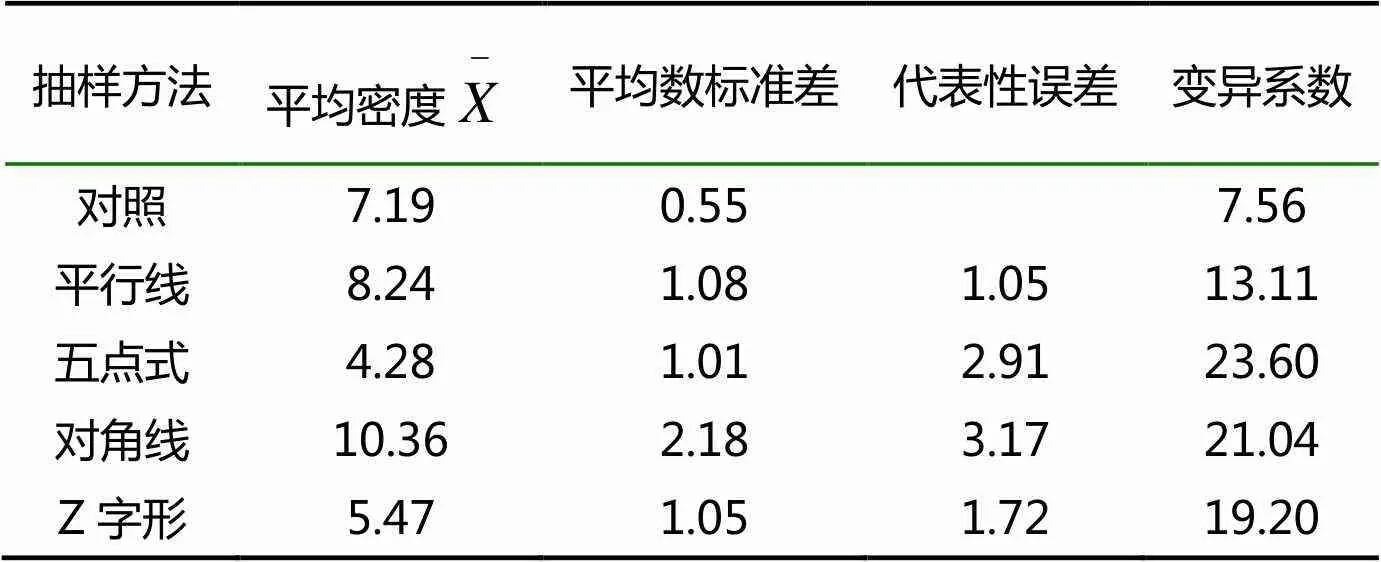
表2 不同抽样方法准确程度比较
由上表各计算数据可见,在4种不同的抽样方式中,以平行线法取样较接近于实际情况,相对5点式取样误差较大,在实际应用中一般不采用。
从实际中分析造成这种现象的原因是平行线法抽样点分布均匀,增加了与分布核心相遇的机会,有较好的代表性,而五点式取样则不具备以上优点,从整体水平而言,代表性较差。
2.2 理论抽样数确定
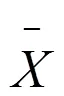

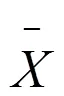
将α=1.38 β=4.28 代入上式整理得;
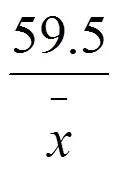
2.3 序贯抽样方法的应用
按照 Iwao的序贯抽样方法(1975)设 m0为害虫的防治指标,那麽在特定 t 值下对应抽样数 n 时被抽取的害虫总数的上、下界为:
T=nm0±t√n(α+1)m0+(β-1)m02
α=1.38 β=4.28 t=1.96代入上式整理得:
T=nm0±√n(9.14m0+12.60m02)
在实际应用中,一定抽样数下的累计虫数与上式计算的上、下界值进行比较,若累计虫数超过对应上界值,就必须进行防治,若累计虫数低于对应下界值,则不必进行防治;若累计虫数刚好在上、下界之间时,应继续增加抽样数,直止达到最大抽样数。
Nmax=t2/d02〔(α+1)m0+ (β+1)m02〕
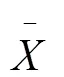
3 小结与讨论
3.1 分析造成梨木虱若虫聚集分布的原因主要是因为梨木虱1年多代,繁殖量大,成虫产卵成片,若虫主动迁移能力差,个体间无竞争残杀及林间喷施药不均匀造成。
3.2 根据梨木虱卵和若虫的聚集分布的特点和其生物学特性,在防治策略上必须抓好预测预报,并集中力量消灭害虫在初发期,控制核心扩散、蔓延。
[1]丁岩钦. 昆虫种群数学生态学原理与应用[M].北京:科学出版社,1980.
[2]徐汝梅. 昆虫种群生态学[M]. 北京:北京师范大学出版社,1987.
[3]邬祥光. 螟虫调查取样方法的比较研究[J].植物保护学报,1963,2(2):141-148.
S763.35
A
1003-2630(2010)04-0031-03
2010-10-25
(责任编辑:王团荣)
——纪念上山下乡48周年

