任意多边形平面载流线圈磁场的空间分布

岑敏锐

(武汉工程大学理学院，湖北 武汉 430074)

0 引 言

载流线圈空间磁场分布的计算是电磁学中的一个常见问题，在各种形状的载流线圈中，具有轴对称性的圆形载流线圈研究得比较多[1-5]，而对不具有轴对称性的多边形载流线圈的磁场问题则研究得很少，且仅限于一些特殊的多边形[6-8].本文根据一段载流直导线在空间某点的磁场矢量公式，将多边形载流线圈视为多段载流导线，然后根据场强叠加原理，给出了求任意多边形平面载流线圈在空间任意点的磁场分布的方法，并且运用这种方法求出了任意多边形平面载流线圈磁场的空间分布的普遍表达式.

1 一段载流直导线在空间某点的磁场矢量公式

如图1所示，一段载流直导线在空间某点P处产生的磁感应强度B的大小为：

(1)

B的方向与电流的方向成右手螺旋关系.

如果只需要求一段载流直导线的磁场分布，根据(1)式，只要知道电流强度I，P点到导线的垂直距离r0，导线与导线端点到P点连线的夹角θ1和θ2，就可以进行求解.但如果需要求的磁场分布是由多段载流直导线组成的多边形载流线圈所产生的，由于磁感应强度是矢量，而(1)式只考虑了大小，在求空间某点P处的总磁感应强度时，有必要将其改写为矢量式.

图1 一段载流直导线的磁场分布

设图1中载流直导线的长度为d，从P点指向导线两端点的矢量分别为r1和r2，则点P处的磁感应强度的方向和r1×r2矢量的方向相同.考虑方向后，(1)式中的磁感应强度可以写成矢量式(2).

(2)

(3)

根据三角形的余弦定理得：

(4)

(5)

(6)

将(4)式、(5)式和(6)式代入(3)式中得：

(7)

如图2所示，载流直导线P1P2位于Oxy平面之内，从空间某点P(x，y，z)指向P1(x1，y1，0)和P2(x2，y2，0)的矢量分别为r1和r2.

式(7)中矢量r1和r2以及导线长度d分别为：

r1=(x1-x)i+(y1-y)j-zk

(8)

r2=(x2-x)i+(y2-y)j-zk

(9)

(10)

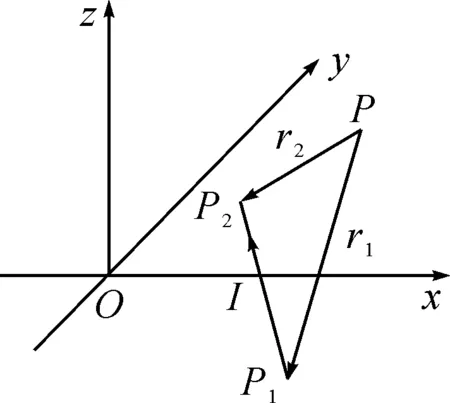
图2 OXY平面内一段载流直导线的磁场分布

将(8)、(9)和(10)式代入(7)式中得：

(11)

(11)式即为要求的一段载流直导线在空间某点的磁场矢量公式.其中，R、D1和D2分别为：

R=[(x1-x2)2+(y1-y2)2]z2+[(y1-y2)x-

(x1-x2)y+(x1y2-x2y1)]2

(12)

(x1x2+y1y2)]

(13)

(x1x2+y1y2)]

(14)

根据(8)式和(9)式可以算出矢量r1×r2在三个坐标轴上的分量分别为：

|r1×r2|x=z(y2-y1)

(15)

|r1×r2|y=z(x1-x2)

(16)

|r1×r2|z=x1y2-x2y1+xy1-x1y+x2y-xy2

(17)

将(15)、(16)和(17)式代入(11)式中可以求出多边形任一条边在空间某点P处产生的磁感应强度在三个坐标轴上的分量分别为：

(18)

(19)

(20)

在求出多边形任意边在空间某点P处产生的磁感应强度后，根据场强叠加原理，就可以求出整个线圈在空间的磁场分布.下面以菱形平面载流线圈为例，按照以上方法求出该线圈在空间的磁场分布.

2 菱形平面载流线圈磁场的空间分布

如图3所示，设有一菱形载流线圈ABCD位于OXY平面之内，各顶点坐标分别为A(a，0，0)、B(0，b，0)、C(-a，0，0)、D(0，-b，0).根据(18)到(20)式分别求出AB、BC、CD和DA四条边在空间某点P(x，y，z)产生的磁感应强度，再根据场强叠加原理可以求出整个菱形平面载流线圈在P点的磁场分布.

图3 菱形平面载流线圈的磁场分布

(21)

(22)

(23)

3 结 语

根据以上分析结果，对于任意多边形平面载流线圈，只要知道其各顶点在OXY平面上的坐标，代入(18)到(20)式中再求代数和即可得到该载流线圈在空间任意点的磁场分布.方法简单、明了，易于理解，可以应用到普通物理的教学中.

参考文献：

[1]李海，张玉颖．圆形线电流的磁感应强度[J].大学物理，1999，18(6)：20-22.

[2]曾令宏.张之翔. 圆环电流的磁场以及两共轴圆环电流之间的相互作用力[J].大学物理，2002，21(9):14-16，41.

[3]朱平.圆电流空间磁场分布[J].大学物理，2005，24(9):13-17.

[4]张星辉.圆电流磁感线的分布及磁感应强度的函数表达式[J].大学物理，2006，25(1):32-37.

[5]刘耀康.导出圆电流的磁感应强度的简便方法[J].大学物理，2007，26(7): 32-33.

[6]邓卫娟，李秉宽.正三角形载流线圈的空间磁场分布[J].广西物理，2007，28(2): 35-37，39.

[7]邝向军.方形载流线圈的空间磁场计算[J].物理与工程，2006，16(1):18-20，25.

[8]岑敏锐. 同轴等大方形线圈的互感系数[J].武汉工程大学学报，2007，29(4):90-92.