基于窄带步进频率的旋转目标三维ISAR成像

李 军 刘亚波 邢孟道 郭 睿 李亚超

(西安电子科技大学雷达信号处理重点试验室 西安 710071)

1 引言

随着雷达的不断发展，对大尺寸目标如飞机、卫星等探测已较为成熟，但是在宇宙空间探测等应用领域，弱小目标如空间碎片等的探测仍存在众多难题有待进一步解决。小目标和空间碎片等复杂运动目标既存在平动也存在高速转动，在有限散射点并且散射特性近似不变的前提下，如何对其成像目前已成为各国研究的热点。文献[1]提出利用窄带信号并结合单距离多普勒干涉(SRDI)方法对高速自旋目标进行二维成像。为了提高分辨率文献[2]提出了利用单距离匹配滤波CLEAN(SRMF-CLEAN)方法对高速自旋目标进行二维成像。文献[3]提出利用宽带信号结合广义Radon变换对高速自旋目标进行三维成像。

小尺寸目标成像要求距离分辨率较高，一般通过增加信号带宽提高距离向分辨率，但直接发射大带宽信号对系统要求较高，系统结构复杂且成本高。通过步进频率合成[4,5]可以发射不同载频的窄带信号最终达到宽带效果，实现距离高分辨，它对系统要求低，结构简单并且成本低，近年来受到越来越多的重视。采用步进频率合成关键在于距离合成算法及运动补偿，文献[6]提出了步进频率合成旁瓣抑制技术，文献[7-9]提出了合成距离包络法、时域合成算法及频域合成算法。文献[10]提出了参数化的运动补偿算法，文献[11, 12]提出了基于非参数化的运动补偿算法。上述合成算法都基于小角度转角成像，对于高速自旋目标由于其自旋引入的多普勒将影响距离合成的性能[13]，常规合成方法不再适用，严重时甚至不能成像。

针对上述问题，本文提出了一种基于窄带步进频率信号的自旋目标三维成像算法，首先对窄带子脉冲利用单距离匹配滤波进行二维成像，然后结合CLEAN 算法[14]确定散射点个数及其半径、角度，最后在子脉冲二维像之间利用频带合成技术提高距离分辨率，最终实现三维成像。此方法避免了高速旋转目标所引起的多普勒变化对距离合成时的影响，并且对窄带自旋目标的处理无需引入广义Radon变换进行二维曲线积分，减小了算法复杂性。通过多点目标仿真验证了本文算法的有效性和可行性。

2 窄带步进频率高速自旋目标模型

空间目标沿x轴以v速度运动，沿z轴以ω高速旋转，雷达射线与旋转轴夹角为α，如图1所示，P点为空间目标上某散射点，O为目标载体坐标系的原点。

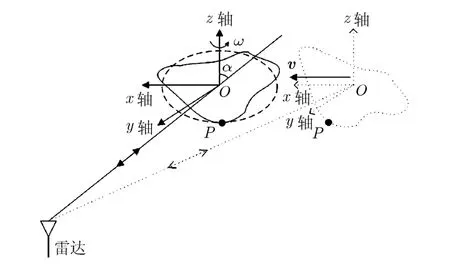
图1 空间旋转目标运动示意图

设雷达发射波形为步进线性频率调制信号，一组步进频频由M个chirp子脉冲组成，第m个子脉冲信号形式如下：

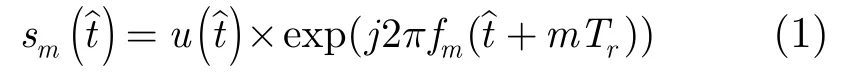
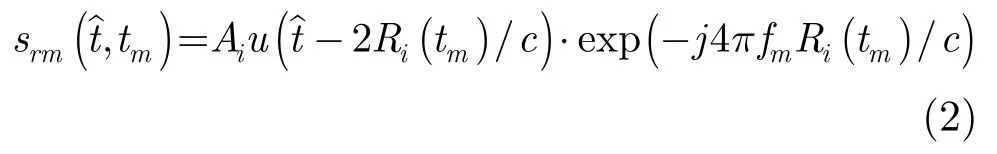
式(2)中iA为回波幅度，c为电磁波传播速度，为第m个子脉冲的方位慢时间，为各子脉冲统一的慢时间。

将回波转换到距离频域，信号为

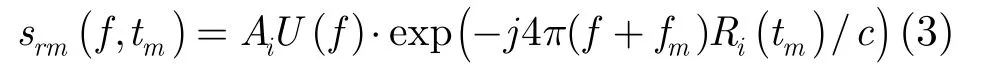
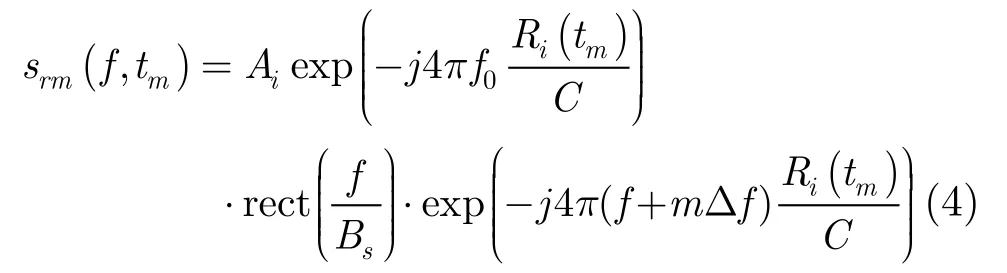
对式(4)进行逆傅里叶变换转换到时域为

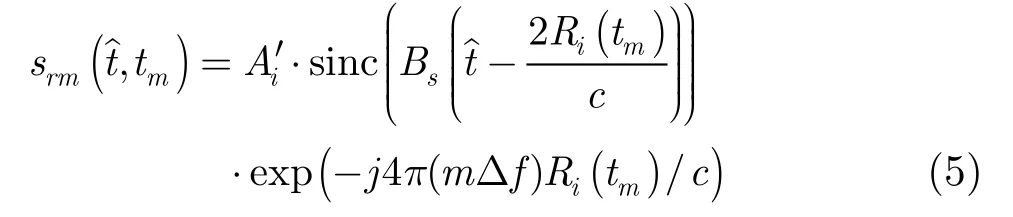
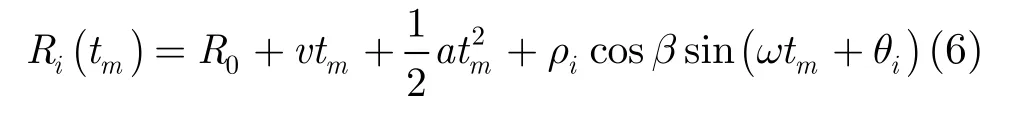
其中R0为初始距离，v为目标速度，a为目标加速度，ρi为目标旋转半径，θi为初始角度，ω为旋转角速度，β为雷达射线与目标自转轴夹角。

窄带信号的ISAR成像主要利用目标的转动分量，平动分量对成像没有贡献需要进行补偿。文献[15]提出了参数化的运动补偿算法对速度和加速度分别补偿，本文的侧重点不在运动补偿而在三维成像算法，假设平动分量已得到补偿。注意式(6)中的转动分量会引入额外的多普勒，此项如果直接用于距离合成将降低合成性能，增大副瓣，随着高速自旋半径的增大将严重影响距离合成，最终导致不能ISAR成像。

3 步进频率高速自旋目标三维ISAR成像算法

在有限散射点的模型下，假设目标的散射特性在自旋过程中近似不变，经过平动补偿后，则N点目标的距离脉压后回波频域波形公式如下：

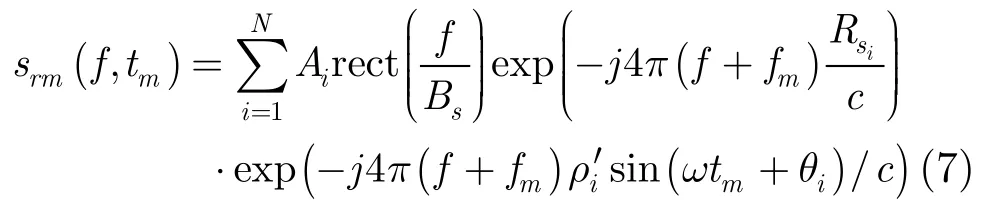
分析式(7)可知，目标转动引起距离频谱与方位慢时间的非线性耦合，每个散射点由于其半径及相位的不同耦合程度也不同。直接采用频域合成与频谱重叠运动补偿将破坏转动分量在频域的分布。

为了减小散射点之间的相互影响，这里先对窄带信号进行单距离匹配滤波，针对逐个旋转半径，建立rk匹配模型：

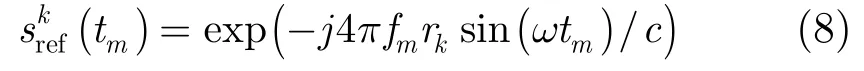
构建式(8)需要估计自旋速度ω，根据文献可以直接采用时域互相关方法或频域二维相关估计ω，采用快速傅里叶变换实现匹配滤波以增加运算效率，假设旋转半径rk上有L个散射点，匹配滤波后的信号为

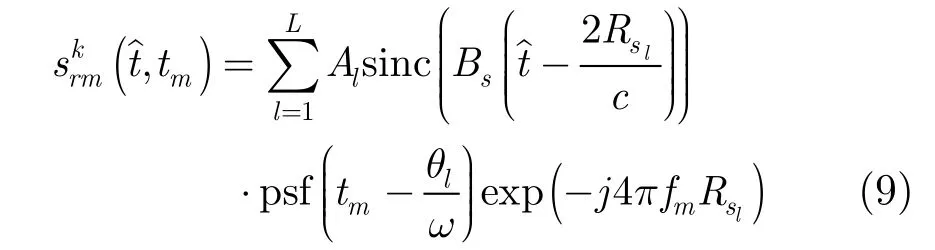
图2 单距离匹配滤波示意图

由式(9)可知，不同散射点因旋转半径及初始相位的不同在 ISAR像里得以区分，但由于发射的窄带信号，距离分辨率较差。在去除了不同散射点距离频率与慢时间的耦合后，可以通过距离合成提高距离分辨率。这需要二维ISAR像散射点的个数，本文结合CLEAN技术直接估计散射点位置及初始旋转相位。

首先在二维复图像中提取最大峰值对应的两个参数r,θ作为其中一个散射点位置估计，然后以估计的位置参数构造其点散布函数为

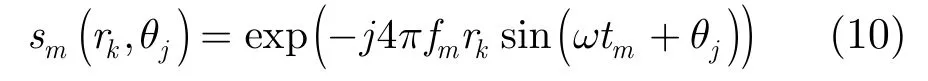
利用最小范数准则估计该点的反射系数为

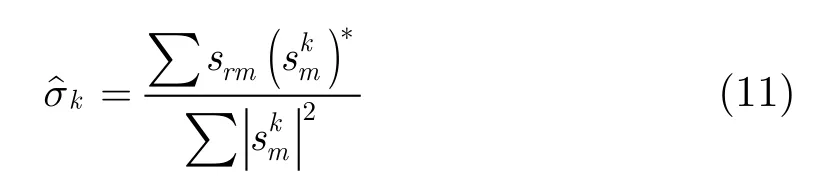
为了使估计的参数更加准确，可以通过局部搜索的方法提高估计精度，即搜索使下式(12)能量最小的半径与角度：

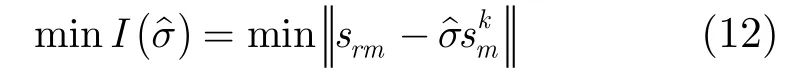
在原始信号中减去该点的贡献，得到

重复上述步骤直到式(12)的信号残余能量低于某门限值时截止。

选取所有距离单元分别进行二维成像，注意为了步进频率二维像之间的微小差异，只需对某个步进进行上述CLEAN及搜索，其他步进频率直接按搜索的半径和相位求反射系数即可。针对某个散射点p，进行频率域的距离合成，即距离时域乘以频域因子：

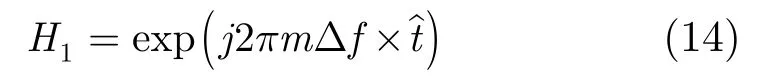
为了防止频谱混叠，需要在频域对信号进行两端补零，然后进行频谱搬移，最后对M个子脉冲求和。假设频率步进量Δf与子脉冲信号带宽Bs相等，得

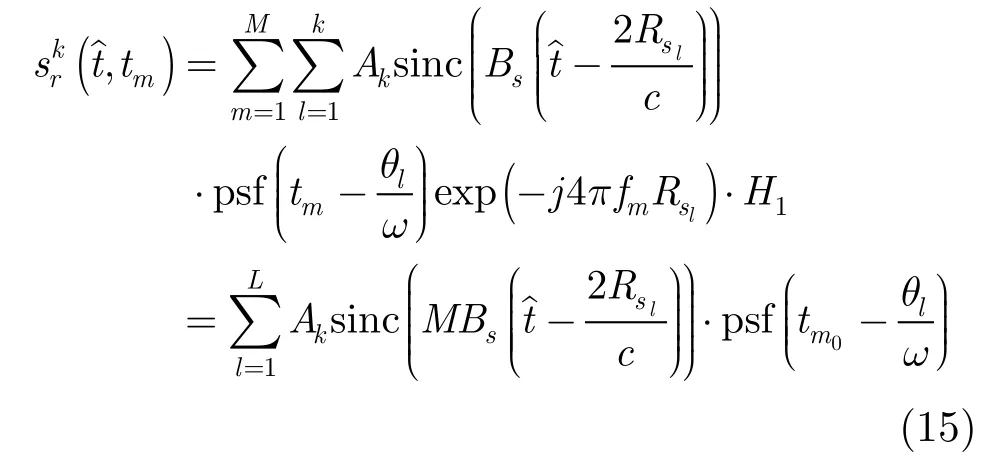
从式(11)可以看出，距离分辨率比合成前提高了M倍。对CLEAN后的散射点分别沿距离向进行距离合成，提高距离分辨率，最终实现三维成像。

总结上述处理步骤，本文算法流程图如图3所示。

4 仿真结果与分析

为了验证本文窄带步进频率的三维成像算法，设置系统仿真参数，步进频率子脉冲带宽为 50 MHz，理论分辨率为3 m，一组子脉冲共10个步进，步进量也为50 MHz。设置6个独立高速自旋散射点，并假设其散射特性近似不变，在圆柱坐标系下旋转半径、初始角度及高度分别为(0.5,0,1)，(0.5,2π/3,1)，(0.5,-2π/3,1)，(1,0,0)，(1,2π/3,0)，(1,-2π/3,0)，发射系数均为1，散射模型结构如图4所示：

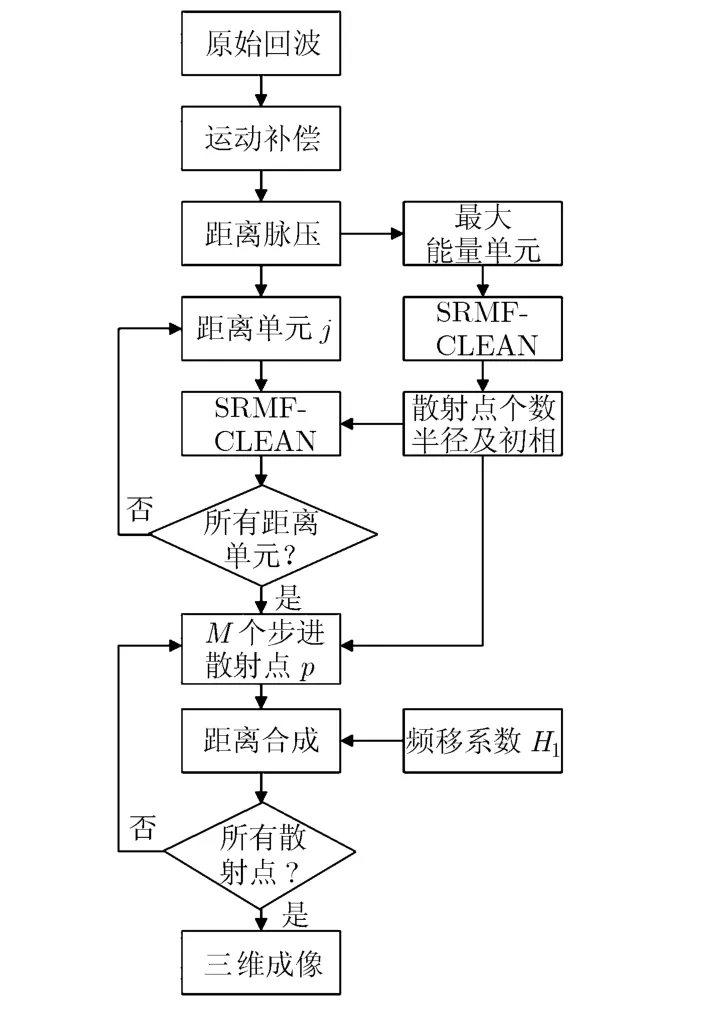
图3 三维成像流程图

散射点自旋速度为 2转/秒，系统采样率设为50 MHz，雷达与旋转轴之间夹角为45°，由于顶层3个散射点与底层3个散射点间距为1 m，投影到雷达射线为0.7 m，而雷达窄带子脉冲的分辨率为3 m，因此所有散射点均在一个分辨单元内，顶层与顶层无法分离。

直接采用单距离匹配滤波，成像结果如图5所示：

从图6中可以明显看出6个散射点，但由于副瓣的影响，有可能淹没弱散射点的主瓣，这里结合CLEAN算法逐个搜索散射点，得到图6成像结果。搜索得到6个散射点及其参数信息如表1所示。

可见结合CLEAN技术后可以提高目标识别能力，搜索结果与参数基本一致。由于所有散射点均在一个窄带距离分辨单元内，最终得到二维成像结果如图7所示。

利用多个距离单元的二维 ISAR像及频域距离合成技术，对某不同旋转平面上两个散射点分别进行距离合成，图8为距离合成前后目标在距离上的分布。

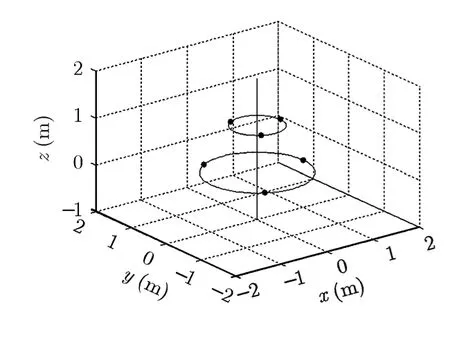
图4 点目标模型

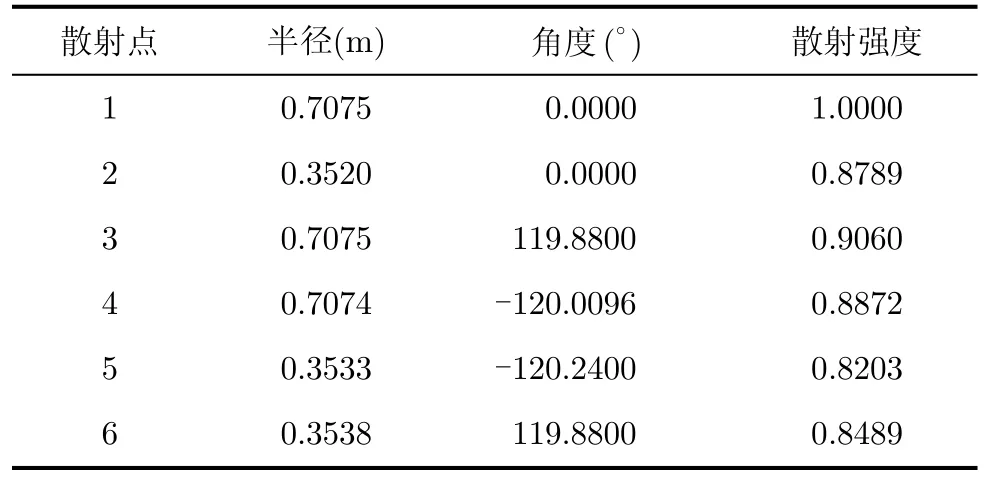
表1 SRMF-CLEAN成像结果

距离合成前，目标分辨率为3 m，所有散射点在同一分辨单元内，距离合成后，理论的距离分辨率为 0.3 m，图 8(b)中顶层散射点与底层散射点可以明显分开，间距为0.7 m，与实际位置相符。将6个散射点沿xyz坐标系下分布得到合成前后的三维成像结果如图9所示。

可以看出本文方法三维成像与窄带三维成像结果相比有较大提高，注意仿真时雷达位于散射点上方，其三维成像结果与点目标模型反向，但散射点的旋转半径及初相仍保持不变。

5 结束语

常规三维空间旋转目标成像利用宽带信号进行Radon变换和曲线积分，算法复杂且对系统配置要求高。本文从原理上验证了利用窄带步进频率信号也可以进行三维旋转目标成像，算法简单，且发射窄带信号对系统结构要求较低。在运动补偿的前提下首先进行常规的窄带自旋目标成像，然后利用距离合成技术对复图像进行三维合成，最终得到三维图像。多点目标三维成像仿真验证了算法的可行性，但由于目前条件的限制还没有实测数据，算法仿真的有效性为今后的工程实现提供了一定的理论参考。

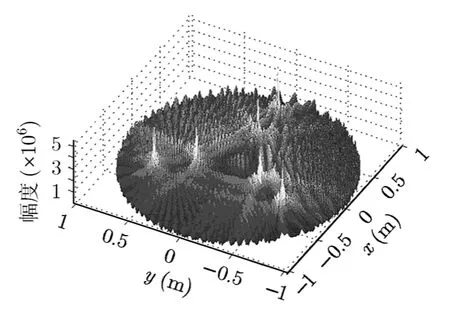
图5 6 个散射点的SRMF 成像

图6 SRMF-CLEAN成像

图7 点目标二维成像

图8 两点目标距离合成示意图

图9 步进频率合成前后三维成像

[1] Sato T. Shape estimation of space debris using single-range Doppler interferometry.IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(2): 1000-1005.

[2] Wang Qi, Xing Mengdao, Lu Guangyao, and Bao Zheng.SRMF-CLEAN imaging algorithm for space debris.IEEE Transactions on Antennas Propagation, 2007, 55(12):3524-3533.

[3] Wang Qi, Xing Mengdao, Lu Guangyao, and Bao Zheng.Three-dimensional radar imaging for rapidly spinning targets.IEEE Transactions on Geoscience and Remote Sensing, 2008,46(1): 22-30.

[4] Berizzi F, Martorella M, and Bernabo M. A range profiling technique for synthetic wideband radar.IET Radar Sonar Navigation, 2008, 2(5): 334-350.

[5] González-Blanco P, De Diego E, Millán E, Errasti B, and Montiel I. Stepped-frequency waveform radar demonstrator and its jamming. 2009 International Waveform Diversity and Design Conference, Kissimmee, Florida, USA, 2009: 192-196.

[6] Gladkova I and Chebanov D. Grating lobes suppression in stepped-frequency pulse train.IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1265-1275.

[7] Chen H, Liu Y, and Li X. Mathematics of synthesizing range profile.IEEE Transactions on Signal Processing, 2007, 55(5):1950-1955.

[8] Lord R T and Inggs M R. High resolution SAR processing using stepped-frequencies. IGARSS, Singapore, 1997:490-492.

[9] Wilkinson A J, Lord R T, and Inggs M R. Stepped-frequency processing by reconstruction of target reflectivity spectrum.Proceedings of the 1998 IEEE South African Symposium on Communications and Signal Processing, Cape Town, South Africa, Sep. 7-8, 1998: 101-104.

[10] Jeong Ho-ryung, Kim Hyo-tae, and Kim Kyung-tae.Application of subarray averaging and entropy minimization algorithm to stepped-frequency ISAR autofocus.IEEE Transactions on Antennas and Propagation, 2008, 56(4):1144-1154.

[11] Wang Y, Ling H, and Chen V C. ISAR motion compensation via adaptive joint time-frequency technique.IEEE Transactions on Aerospace and Electronic Systems, 1998,34(2): 670-677.

[12] Berizzi F, Martorella M, and Cacciamano A. A contrast-based algorithm for synthetic range-profile motion compensation.IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3053-3062.

[13] He Si-san, Zhu Yong-feng, and Zhao Hong-zhong,et al..Analysis of rotating structures for stepped frequency radar.2008 International Conference on Radar, Adelaide, Australia,sep. 2-5, 2008: 386-390.

[14] Tsao J and Steinberg B D. Reduction of sidelobe and speckle artifacts in microwave imaging: the CLEAN technique. IEEE Transactions on Antennas Propagation. 1988, 36: 543-556.

[15] Yau D, Berry P E, and Haywood B. Eigenspace-based motion compensation for ISAR target imaging. EURASIP Journal on Applied Signal Processing, 2006, Article ID 90716: 1-9.