混凝土自锚式悬索桥静力特性分析
黄斌勇 邵 敏
自锚式悬索桥是高次超静定结构体系,它不仅具有传统悬索桥的力学特征,而且由于主梁受到巨大的轴向压力,主梁存在着压弯效应,使得其几何非线性更为严重,在各种外荷载作用下,自锚式悬索桥的受力性能是决定悬索桥结构设计的主要根据,因此对自锚式悬索桥的成桥状态进行静力性能分析非常必要。
本文以位于浙江省的某混凝土自锚式悬索桥实桥为例,进行该桥的力学性能研究。该桥主桥跨径布置为40 m+118 m+40 m,全长198 m,宽 24 m。该桥梁设计荷载等级为城—A级,人群4 kN/m2,设计车速为 30 km/h,桥面布置为 3.0(人行道)+2.0(索面及绿化)+14.0(行车道)+2.0(索面及绿化)+3.0(人行道)=24.0 m。
1 Midas有限元模型建立
1.1 计算模型
本文计算模型基于有限位移理论,用Midas/Civil软件建立三维有限元模型。结合考虑自锚式悬索桥的几何非线性影响。根据各个桥梁构件的形式和受力特点,建模过程中,共采用了三种单元:空间梁单元、索单元和板单元。计算模型中共包含1 038个节点和2 000个单元,见图1。
1.2 大桥各部分的有限元模拟
缆和吊索采用索单元,索塔、加劲梁和横梁采用梁单元,桥面板采用板单元。结构的约束条件是:主塔塔底为固结,主缆在塔顶与主塔的连接按刚性连接考虑,加劲梁梁端根据实际支座布置形式,确定主梁约束情况;加劲梁在主塔处设置的约束,也以实际支座布置情况设置主从约束。
2 实桥静力特性分析
2.1 恒载效应分析
恒载效应计算分析中,混凝土容重为26 kN/m3,二期恒载包括桥面铺装、防撞墙、人行道栏杆以及人行道铺装等荷载,通过面荷载施加在桥面板上,2 kN/m2。
根据以上建立的模型,计算分析自锚式悬索桥在成桥状态结构恒载作用下的加劲梁、主缆、吊杆、索塔等构件内力及应力。
在恒载作用下,桥梁结构的变形较小,最大竖向变形发生在主跨跨中,为7.0 cm,最大纵向位移发生在塔顶,为 2.0 cm。
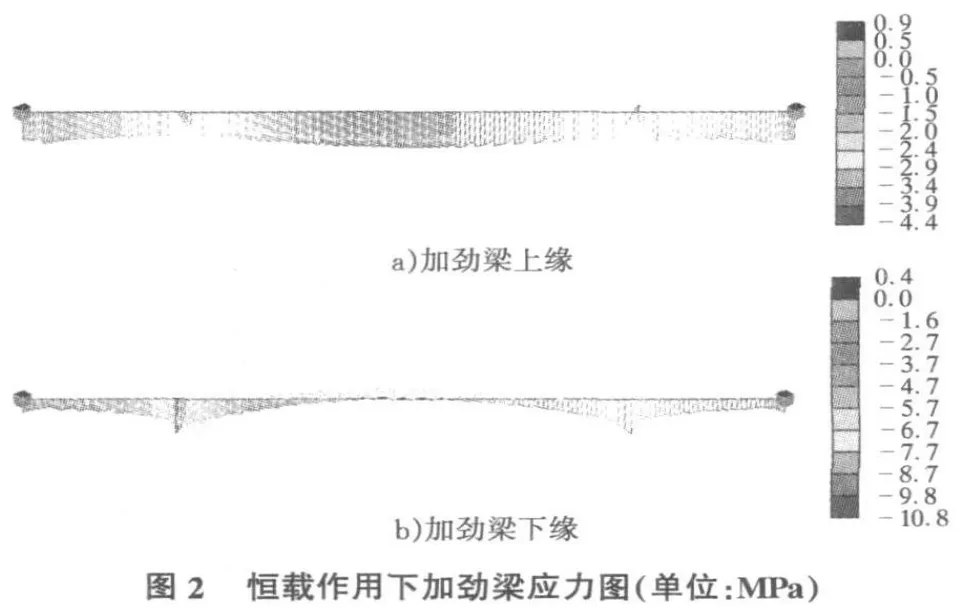
图2为主梁在恒载作用下的应力图。可见,加劲梁应力比较均匀,上缘基本受压,上缘最大压应力在主跨跨中,为4.4 MPa;下缘在跨中出现了0.4 MPa的拉应力,最大压应力为10.8 MPa,为靠近塔柱处。加劲梁的应力均在合理范围内。
桥塔在恒载作用下,基本处于中心受压状态,主塔最大压应力为-10.1 MPa,位置在上塔柱与下横梁相交处,满足规范要求。
主缆在恒载作用下,应力在214.1 MPa~259.7 MPa之间,应力均匀且均在合理范围内。恒载作用下,吊杆应力在149.2 MPa~196.7 MPa之间。
通过以上计算分析可知,在恒载作用下,自锚式悬索桥的位移较小,加劲梁的应力、主缆以及吊索的应力均匀,均满足要求。
2.2 活载效应分析
全桥根据设计布置为机动车道四车道(双向),人行道二车道(每侧一道)。在有限元分析中考虑偏载布置机动车道,人行道按照满布行人来考虑。实际计算时按照四(机动车道)+二(人行道)=六车道来布置。
车辆荷载取值:城市—A级,根据实际结构形式进行横向汽车荷载多车道加载。人群荷载取值按照CJJ 11-93城市桥梁设计准则取值,最不利组合为四车道(折减)+二人行道荷载。
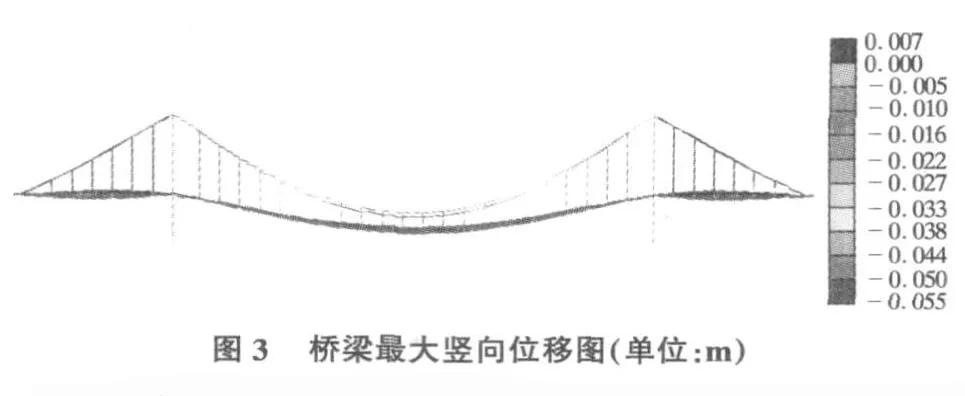
从图3中可以看出,活载作用下主跨加劲梁跨中竖向最大下挠为55 mm,参考《公路悬索桥设计规范》(送审稿)中390 mm的要求(L/300,L为跨度,本桥中跨为118 m),主跨结构满足挠度要求;纵向最大位移为桥塔顶部,为11 mm。
车道、人群荷载作用下,加劲梁的最大弯矩与最大轴力均出现在主跨约1/4处,约为1 800 kN◦m和 2 200 kN。活载作用下桥塔最大弯矩出现在桥塔根部,约 5 600 kN◦m。
桥梁使用阶段,主缆和吊索产生的拉应力均匀且值不大,主缆和吊索受力状况良好。
在最不利活载的作用下,边跨支座出现了负反力,因此需要对边跨端部进行压重。
[1]杭州市城建设计研究院.江山市北关大桥工程扩大初步设计[R].2003.
[2]Midas/Civil用户手册[Z].北京:北京迈达斯技术有限公司,2003.

