一类多险种复合Poisson-Geometric过程风险模型研究

李应求 ，甘 柳 ，魏 民 ，2

(1.长沙理工大学a.数学与计算科学学院；b.经济管理学院，长沙 410076;2.中国工商银行湘潭湘江支行，湖南 湘潭 411101)

1 预备知识及模型定义

经典风险模型中索赔来到过程是一个Poisson过程,Poisson过程的一个重要性质是均值等于方差，但在保险公司的实际运作中是难以具备这样的性质的。为了使模型更加符合实际，文献[2]提出了一类称为复合Poisson-Geometric过程的计数过程，建立了如下模型:

其中U(t)为保险公司在t时刻的盈余量，c为单位时间内收取的保费，u≥0 为公司的初始盈余，{N(t)；t≥0}是参数为，ρ的复合Poisson-Geometric过程，Xi表示第i次索赔额。针对模型(1)，文献[2]给出了其破产概率所满足的更新方程，并在索赔额服从指数分布时，得到了破产概率的显示表达式;文献[3]在索赔分布Xi为相位分布的情况下，得到了破产概率的显示表达式，并进行了数值计算;文献[6]得到了Gerber-Shiu折现罚金函数;文献[7]给出了破产概率上界估计。文献[8]将模型(1)推广，建立了如下模型:

其中{M(t)，t≥0}为 Poisson 过程，并得到了模型(2)的破产概率上界。文献[10]建立了一种多险种模型:

其中每个险种的索赔来到过程{Ni(t)；t≥0}都是参数为λi，ρi复合 Poisson-Geometric 过程，保费来到次数{Ki(t)；t≥0}是参数 αi为的 Poisson 过程，i=1， …，n，{W(t)，t≥0} 是标准的Wiener过程，σ为扰动强度，并得到了破产概率所满足的Lundberg不等式和破产概率上界。

本文将模型(3)进一步推广，建立了模型如下:

其中保单的收入为随机变量Yij。假定:Yij相互独立，与Yi同分布，分布函数为Fi(x)，期望为 mi，其二阶矩存在;理赔额Xij相互独立，与 Xi同分布，分布函数为 Gi(x)，期望为 μi，且其二阶矩存在;以上随机过程和随机变量序列都相互独立。我们称{X(t)，t≥0}为多险种复合Poisson-Geometric风险模型。

模型(4)与(3)的区别在于:保费的收取不再为常数，而是独立同分布的随机序列。

实际背景:Ki(t)表示在时间段内(0，t]内保险公司第i个险种的保单数，保费的收取不为常数，而是独立同分布的随机序列，第i个险种的保费收入为Yij，保险公司可以根据历史数据确定各个险种的其分布；第i个险种理赔额随机变量Xij，分布函数为Gi(x)，W(t)表示保险公司不确定支付和收益。

本文给出了模型(4)的破产概率所满足的Lundberg不等式及一般表达式。最后得到了模型 (4)在双险种情况下的Gerber-Shiu折现罚金函数。

为了保证保险公司的经营稳定，每个险种的单位时间内的保费收入应都大于其单位时间内的理赔，即：

本文恒设式(5)成立。

定义 1 设 λ＞0，0≤ρ＜1，称{N(t)；t≥0}是参数为 λ，ρ 的复合Poisson-Geometric过程，如果：

(1)N(0)=0

(2){N(t)；t≥0}具有平稳独立增量

(3)对 t≥0 有 N(t)～PG(λt，ρ)

注3：当ρ=0时，复合Poisson-Geometric过程退化成Poisson过程，可见前者是后者的推广。

2 最终破产概率上界

容易验证，由(4)定义的风险过程是具有性质:

性质1 (1)X(0)=0 P-a.s.

(2){X(t)；t≥0}具有平稳独立增量

(3) 存在正数 r，使得 E[e-rX(t)]＜∞

定理1 对于模型(4)，存在函数g(r)，使得E[e-rX(t)]=etg(r)

证明因为：

故有E[e-rX(t)]=etg(r)。定理结论得证。□

定理2 方程存在唯一的正解。

证明 由式(6)可得：

又因为 MXi(r)是递增的，且有 0＜ρi＜1，所以存在 ri＞0，使MXi(r)=1/ρi，当 0＜r＜ri时，0＜MXi(r)＜1/ρi(i=1，2，…，n)，取 r0=min(r1，r2，…，rn)故当 0＜r＜r0有 g''(r)＞0。 且 r→r0时有 g(r)→∞，故 g(r)为一下凸函数，则方程g(r)存在唯一的正解R，且0＜R＜r0。

定义2 称R为调节系数。

设保险公司初始准备金为u，破产时刻为Tu=inf{t≥0|u+X(t)＜0}。 相应的最终破产概率定义为 ψ(u)=P(Tu＜∞)。 定义=σ{X(v);v≤t}。

引理1 Tu是的停时

定理3 令Mu(t)则{Mu(t)，，t≥0}是鞅

证明 由于对任意的t＞v，我们有：

于是定理结论得证。□

定理4 在初始资本为u的条件下，最终破产概率为：

且有 ψ(u)≤e-Ru。

证明 Tu为破产时刻，又对于固定时刻t0，TuΛt0为有界停时，由有界停时

定理，我们有：

这样式(8)就化为了式(7)。□

3 Gerb er-Sh iu折现罚金函数

为了简化问题的讨论，我们现将多险种模型退化为双险种的情况，且保费收入退化为常数，这样我们有盈余过程

在破产发生情况下，我们把破产时刻的赤字记为|U(T)|，破产前瞬时盈余记为U(T-)，记：

式(10)被称为Gerber-Shiu折现罚金函数，由 Gerber和Shui于 1998 年提出， 其中 v∈(0，1]表示折现因子，ω（X，Y）是有界实函数，称之为罚金函数，1A是示性函数。

这里我们记F*n(x)=x-t)dF(t)，n≥1为索赔分布 F(x)的 n重卷积，G*n(x)=(x-t)dG(t)，n≥1为索赔分布 G(x)的 n重卷积，其密度函数f(x)，g(x)的n重卷积分别记为 f*n(x)=x-t)df(t)，n≥1 和 g*n(x)=x-t)dg(t)，n≥1。

定理5 在满足(5)的条件下，模型(4)的Gerber-Shiu折现罚金函数ψ(u，ω,v)满足下列更新方程：

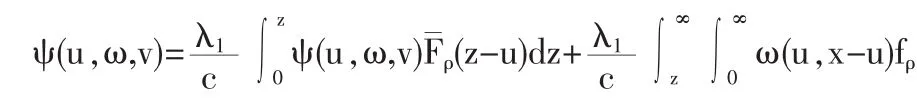
证明 对于充分小的时间Δt，我们考虑(0，Δt]内发生索赔的情况，分成四种情况:1.两个险种都没有发生索赔，2.第一个险种没有发生索赔，第二个险种发生1次以上索赔，3.第二个险种没有发生索赔，第一个险种发生1次以上索赔，4.两个险种都发生一次以上索赔，根据文献[2]引理6，这种情况相对Δt是高阶无穷小。这样，有全概率公式和文献[2]引理6，我们有：

整理得：

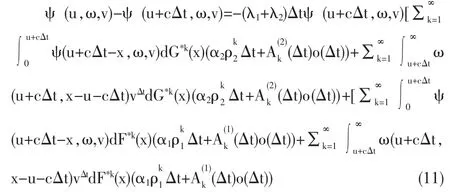
对式 (7)利用泰勒公式，然后两边同时除以cΔt，并令Δt→0，上式化为：

利用文献[2]引理6，交换积分与求和可以交换，这就得到：

注 4 当 ω(X，Y)≡1，v=1 时，容易知道 ψ(u，ω,v)=ψ(u)，即为破产概率。

这样我们有：

推论1 破产概率ψ(u)满足如下更新方程

利用文献[6]中引理3和定理2我们可以得到下面定理:

定理6 破产概率ψ(u)有下面的表达式

[1]Grandell J.Aspects of Risk Theory[M].New York:Springer Verlag,1991.

[2]毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005,26(3).

[3]毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程下破产概率的显式表达[J].中国管理科学,2007,15(5).

[4]李应求,刘朝才,彭朝晖.不确定条件下企业的投资规模决策[J].运筹学学报,2008,12(2).

[5]李应求,林财超,冯荣丽.湖南省产业结构调整的库兹涅茨经验法则实证分析[J].中国经贸,2007,(4).

[6]廖基定,龚日朝,刘再明,邹捷中.复合 Poisson-Geometric风险模型Gerber-Shiu折现惩罚函数[J].应用数学学报,2007,30(6).

[7]廖基定,刘再明,龚日朝.赔付次数为复合Poisson-Geometric过程的风险模型破产概率上界估计 [J].南华大学学报 (自然科学版),2008,22(3).

[8]刘东海,李博.推广后的复合Poisson-Geometric过程的风险模型下的破产概率[J].湖南文理学院学报(自然科学版),2006,18(2).

[9]彭朝晖,冯荣丽,李应求.湖南省城乡收入差距的基本趋势和影响因素分析[J].长沙理工大学学报(社会科学版),2008,23(1).

[10]于文广,黄玉娟等.干扰条件下复合Poisson-Geometric过程的多险种风险模型下的破产概率[J].山东大学学报(理学版),2008,43(2).