改进的免疫克隆遗传算法研究及其在函数优化中的应用*

宫照煊，王 莉

(辽宁科技大学 电子与信息工程学院，辽宁 鞍山 114051)

对于函数优化问题，传统的经典优化方法大都是基于梯度下降或者需要求解问题的导数。而对于多峰、多态以及求解空间比较大的复杂函数，传统算法的求解效果很有限，甚至无法求解。遗传算法虽然简单易行，并以高效性、隐并行性成为求解优化问题的有效方法[1]，但其为群体中的个体提供进化机会的同时，在某种情况下退化现象也相当明显。近年来，人们在基于生物免疫原理的基础上提出了多种人工免疫系统模型和算法[2]，并应用到自动控制、故障诊断、优化计算等领域。免疫克隆遗传算法是将免疫原理与遗传算法相结合所发展的一种新算法。免疫克隆遗传算法提供记忆细胞，使变异向提高适应值的方向发展，避免了搜索的盲目性。但对于求解一些高精度的复杂函数问题，免疫克隆遗传算法的求解效果欠佳，主要原因是算法在进化后期的局部搜索能力有限，以及种群多样性的快速下降而导致算法过早收敛到最优解的附近，而很难收敛到最优解。针对上述问题，本文提出了一位修正算子来解决算法进化后期存在的问题，并对免疫克隆遗传算法的各个算子都做了相应的改进，最后用标准遗传算法SGA(Standard Genrtic Algorithm)、免疫克隆遗传算法IMGA(Immunity Monoclonal Genrtic Algorithm)以及本文的算法比较，并且与参考文献[6]和参考文献[7]的方法作了比较。实验结果表明，本文的算法收敛速度更快、求解精度更高，并且能有效解决免疫克隆遗传算法后期进化慢的问题。

1 改进的免疫克隆遗传算法计算步骤

1.1 基本步骤的改进

1.1.1 编码

改进的免疫克隆遗传算法采用实数编码来处理算法的编码过程，基于实数编码不会存在二进制编码中的Hamming悬崖问题，并且求解精度要比二进制编码高很多，基于实数编码的遗传算法能很快收敛到最优解附近。

1.1.2 初始化

不论采用离散重组算子还是算数杂交算子，搜索范围只局限于初始群体所确定的最大矩体内。采用混沌初始化方法，利用混沌的遍历性、随机性和内在规律性来最大化初始种群所确定的矩体。混沌初始化在保持种群多样性的同时，对防止算法陷入局部最优解也起到了一定作用。Logist映射：

式中μ取 4，此时的 Logisti映射为在(0，1)区间上的完全混沌状态。产生混沌初始种群的方法：随机初始化x0∈(0，1)，利用式(1)生成混沌序列 x0，x1，x2，…xi(i=1，2，…m)，其中 m 为种群数。 利用混沌序列 x0，x1，x2，…xi生成初始群体 p0，p1，…pi(i=1，2，…m)。

1.1.3 选择

本算法在采用轮盘赌选择法的基础上引入了适应值的非单调标度变换，用来解决种群中出现个别适应值极高的个体时，可能导致这些个体在种群中迅速繁殖的现象，即让一些适应值较小的个体也有参加进化的可能，从而增加种群多样性。在选择算子中采用精英保留策略，现已证明采用精英保留策略的遗传算法能以概率1收敛到问题的最优解[3]。适应值的非单调标度变换：

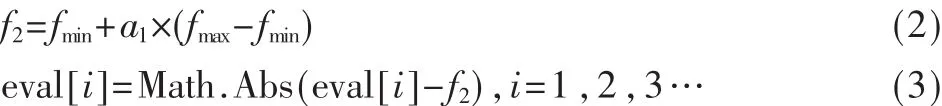
其中fmax为当前适应值最大的个体，fmin为当前适应值最小的个体，eval[i]为当前各个体的适应值[4]。

1.1.4 改进的自适应变异、杂交概率

改进的自适应变异、杂交概率能提高群体中表现优良的个体交叉率和变异率，使得这些优良个体避免出现近似停滞不前的状态，从而增加进化走出局部最优解的可能性。

式中 Pc1=0.9，Pc2=0.6，Pm1=1，Pm2=0.001

因为免疫克隆算子有记忆的功能，使得进化一直向适应值增加的方向进行，所以Pm1=1。

1.1.5 改进的免疫克隆变异杂交

本算法在免疫克隆变异、杂交的基础上考虑了染色体各个基因位对适应值的影响程度。针对函数优化问题，考虑到在进化初期染色体的前几位对适应值的影响相对后几位要大，所以在进化初期算法主要对染色体的前几位进行变异和杂交；在进化后期对染色体的后几位进行变异和杂交，这样做可以大大缩小搜索范围。免疫克隆变异、杂交是将各个体克隆一定数量后进行变异、杂交操作，并且保留原个体信息。将克隆变异、杂交后的个体与原个体比较，选出适应值最高的个体来作为新个体[5]。

1.1.6 位爬山局部搜索算法

免疫克隆遗传算法最主要的特点是能以较快的速度搜索到最优解的90%左右，全局搜索能力强，但是在进化后期的局部搜索能力相对较弱。位爬山算法是一种传统的局部搜索算法，将位爬山算法与免疫克隆遗传算法相结合可以取得较好的效果，本文在传统位爬山算法的基础上提出了一位修正算子，用来改进其在后期搜索过程中的不足，并在仿真实验中得到了满意的结果。

1.2 改进的位爬山算法

传统的位爬山算法过程是[3]：

(1)对于染色体aji=(aj1，aj2，…aji)其中 i∈(1，2，…n)，j∈(1，2，…m)计算个体的适应值：f*=f(aji)，i=1，j=1；

(2)变异各位基因值 ：a′ji=1-aji；

(3)计算新个体适应值：f(a′ji)；

(4)比较新个体适应值：if f(a′ji)＞f*then f*=f(a′ji)

a′ji=(aj1，aj2，…a′ji，aji+1，…ajn)；

(5)循环 i=i+1，返回(2)；

(6)若 i=n，j=j+1 返回(1)；

(7)若 j=m，终止。

位爬山算法存在以下问题：(1)局部最大：某个节点比周围任何一个邻居都高，但是却不是整个问题的最高点。(2)高地(也称为平顶)：搜索一旦到达高地，就无法确定搜索最佳方向，会产生随机走动，使得搜索效率降低。(3)山脊：搜索可能会在山脊的两面来回振荡，前进步伐很小。

对于函数优化问题来说，最优解的每一位数的取值都受其后几位的影响，所以传统的位爬山算法很可能指导算法向偏离最优解的方向搜索。

针对上述问题，本文提出了一位修正算子来改进位爬山算法的不足。具体过程如下：

(1)设aij是利用位爬山算法搜索到的第i个个体中变异第j位基因所得到的最优变异个体。

(2)对于该最优变异个体，在其他位不变的情况下，搜索aij与aij-1的全部组合所得到的个体适应值为evalk，k=0，1，2，…，99aij，aij-1∈(0，9)。

改进的位爬山算法可以以较大的概率避免算法向远离最优解的方向搜索，在进化后期采用改进的位爬山算法搜索到最优解的能力也大大提高了。实验表明，改进的位爬山算法能以较大的概率克服传统位爬山算法的不足，并且能较快收敛到最优解。

2 仿真实验

本文选取了4个具有相当复杂度的测试函数：

F1函数在自变量取值区间内有多个极值点，精确到10-12的最优解为 2.850 273 766 768。

表1 4种函数50次独立实验的统计结果

F2函数有6个局部极小点，其中有 2个点(-0.898，0.712 6)和(0.898，-0.712 6)为全局最小点，最小值为-1.031 628。

F3函数有760个局部极小点，其中有18个全局最小点，最小值为186.73，此函数极易陷入局部极小值185.25。

F4 函数(大海捞针函数)，α∈{0.1，0.01，0.001}随着α的取值不同，此函数形成不同严重程度的模式欺骗问题。当α=0.001时，此函数有无限个局部极大点，其中只有1个点(0，0)为全局最大值点，最大值为1。此函数最大值周围有1个圈脊，取值均为0.990 283，因此此函数非常容易停滞在此局部极大点。本文α取0.001。

对SGA、IMGA以及本文的算法进行了比较，参数选取如下：F1种群数 50，最大进化代数 50；F2种群数100，最大进化代数 50；F3种群数 50，最大进化代数 50；F4种群数100，最大进化代数50。4种函数的50次独立实验结果如表1所示：

从表1中可以看到，由于函数本身的复杂性，SGA的结果是不如人意的。IMGA对于前3个函数能较快收敛到最优解，但由于F4函数具有严重的模式欺骗问题，使得IMGA只能搜索到局部最优。而本文算法在求解精度和求得全局最优解的次数上都远优于SGA和IMGA。

[6]使用一种基于种群划分和杂交的免疫遗传算法对F1函数作了测试，表2为参考文献[6]中的算法与本文算法在独立测试100次后的比较结果：

从表2可以看出，在种群数一样的前提下本文算法与参考文献[6]中的算法都能收敛到最优解，但本文算法利用一位修正算子大大提高了进化后期的收敛速度，因此所需的平均进化代数要比参考文献[6]中的算法少得多。

表2 参考文献[6]算法与本文算法在F1函数上的性能比较

参考文献[7]对遗传算法的各个算子都做了改进，并对F2函数和F4函数作了测试，表3为参考文献[7]算法与本文算法的比较结果。

表3 参考文献[7]算法与本文算法在F2与F4函数上的性能比较

从表3可以看出对于F2函数与F4函数，当进化20代后，本文算法得到的最优解都要优于参考文献 [7]中的算法，在进化到40代时，本文算法都收敛到了最优解。

本文在免疫克隆遗传算法的基础上对各个算子都做了一些改进，并且提出了一种一位修正算子来克服免疫克隆遗传算法在后期搜索方面的不足。实验结果表明本文的算法在收敛速度和收敛精度上远远优于SGA和IMGA，并且通过与参考文献[6]和参考文献[7]中的算法的比较，体现出本文算法在进化代数上的优势。

参考文献

[1]王小平，曹立明.遗传算法理论应用与软件实现[M].西安：西安交通大学出版社：2002.

[2]DU H， JIAO L， WANG S.Clonal Operator and antibody clone algorithms[C].Proceedings of the First International Conferrence on Machine Learning and Cybernetics， Beijing，2002.

[3]张文修.遗传算法的数学基础[M].西安：西安交通大学出版社，2000.

[4]李敏强，林丹，李书全.遗传算法的基本理论与应用[M].北京：科学出版社，2002.

[5]焦李成，刘芳，缑水平.智能数据挖掘与知识发现[M].西安：西安电子科技大学出版社，2006.

[6]武研，李儒耘.一种基于种群划分及杂交的免疫遗传算法[J].计算机工程，2008，2(3)：220-222.

[7]王庆明，宋玉梅.基于改进遗传算法的函数优化及其性能分析.机械设计与制造[J].2007，2(2)：52-54.