基于区域聚合的栅格地形数据简化算法
郭文普,王天宝,徐东辉,臧传收
(1.第二炮兵工程学院,陕西 西安710025;2.第二炮兵驻孝感地区军事代表室,湖北 孝感 432000;3.第二炮兵驻石家庄地区军事代表室,河北 石家庄 050081)
0 引言
随着遥感技术、计算机视觉、计算机图形学等学科的发展,由航空航天摄影测量或其他测量手段获取地形数据来生成具有高分辨率的三维地形模型已经十分普遍。这些由上百万或更多三角形面片表示的各种地形模型,满足了人们对地形真实感所提出的越来越高的要求。但大数据量的三维场景重建对目前的图形硬件而言,实现交互方式的实时绘制是十分困难的。因此,早在上世纪70年代,就提出了对三维网格数据进行简化的思想,即用尽可能少的数据构造原始模型的逼近模型。如文献[1]中提出了一种顶点聚类算法,算法通过将网格分割成小块,每一块中的顶点聚合为一个新顶点来实现简化。文献[2]提出了一种区域合并算法。算法先将网格表面分成若干区域,然后将区域的边界简化成多边形,最后对多边形进行三角剖分,得到简化网格。这些算法面向的应用目的不同,各有优点和不足之处。
目前地形的三维建模方式有很多,但总体上可以分为规则网格建模(如正方形)与不规则网格建模(如TIN,Triangulated Irregular Network)两大类。规则网格建模由于数据结构简单而得到了较为广泛的应用,如常见的DEM(Digital elevation model)数据就采用了规则网格。在借鉴上述简化思想的基础上,针对规则网络的地形数据提出了基于区域聚合的地形数据简化算法。
1 区域聚合数据简化算法
采用规则网格方法时,地形的分辨率相对固定,在地形平坦区域存在数据冗余的现象,如果能有效地消除这些冗余的数据,则可在保持真实精度不变的情况下,简化数据。从这一基本点出发,该算法的设计思想与实现过程如下。
1.1 区域聚合
针对规则网格数据的特点,没有采用其他文献中常用的顶点聚类或区域合并算法,而是采用了区域聚合。即将共面或近似共面的若干地形栅格点用这组栅格点的边界点代替,并进行三角剖分。
1.2 利用最大法向量夹角进行误差度量
地形简化的误差度量是用来量化简化前地形和简化后地形的差异,引导地形数据简化,从而使得简化后的误差在用户允许误差范围之内。如何确定所有顶点或三角面片的重要程度对简化地形模型的拟真度影响很大。有些算法用点到平面的平均距离作为局部误差度量来控制点的删除,有些算法用曲率来计算顶点的重要程度,近年来还有算法采用了体积[3]作为度量误差,本算法采用了三角面间最大法向量夹角余弦值作为简化误差度量。最大法向量夹角θmax,即一组地形栅格点所描述的地形面中每个三角面的法向量间最大的夹角,其余弦值为cosθmax。
由V1、V2、V33个顶点构成的三角面的法向量计算公式为:

N1、N22个法向量的夹角θ的余弦值计算公式为:

进行简化运算时,事先根据简化需求指定简化阈值Ct:

当指定阈值夹角为0°,即Ct=1时,地形数据简化为无失真的简化。
1.3 递归算法实现
采用递归函数实现该地形数据简化算法,以最常见的正方形栅格为例,初始地形聚合区域大小设置为32*32,算法过程可描述为:
①读入栅格地形数据,将栅格地形数据按32*32大小进行分块,对每一块地形数据分别进行后续的递归聚合运算;
②聚合运算函数
Step1:若分块大小为1,即仅为一个栅格点,则中止递归过程,存储该点索引坐标(u,v);
否则:
Step2:计算分块数据的最大法向量夹角θmax的余弦值cosθmax;
Step3:若cosθmax<=Ct,则聚合成功,中止递归过程,存储该聚合区域的4个边角点的索引坐标(u,v);
否则:
Step4:细化分块,即将原分块分成4小分块,对该4小分块分别调用聚合运算函数;
③地形数据中,左侧及下侧条状区域小于初始分块区域大小的栅格点不作简化处理,直接存储这些栅格点索引坐标(u,v);
经上述过程运算后,则可得到简化后的存留的栅格地形数据的索引坐标。
注:索引坐标(u,v)为该点在原栅格数据中的行列号。
1.4 简化后地形数据的绘制
利用简化后存留的栅格地形数据的索引坐标和原始栅格地形数据,求出简化后每个栅格点的真实坐标(x,y,z),这样就得到了原地形数据经简化运算后的一系列散列点。此时,对这些散列点的绘制,一种作法是采用Delaunay三角化过程,构造不规则三角形网TIN(Triangulated Irregular Network),从而实现绘制。这种作法存在2个主要的缺陷,一是TIN的生成过程复杂,二是结构存贮量大。
分析简化算法流程,不难发现这些散列点每4个点即可构成一个平面(斜面),可直接进行三角剖分进行绘制,不需要进行Delaunay三角化,图1为绘制的线框图。

图1 存在地形裂缝的格网
很明显,这种绘制方法存在着大量的地形裂缝,这些地形裂缝存在于每个初始子块及简化时细分的子块间。消除了这些地形裂缝,就可以实现简化后地形数据的绘制了,图2给出了消除子块间地形裂缝的示意图,算法实现时利用存留散列点的坐标索引(u,v)构造地形裂缝间的三角面片即可。
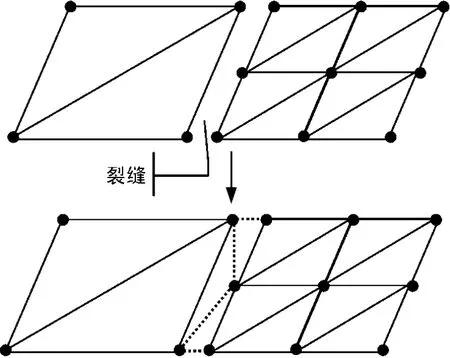
图2 消除裂缝示意图
2 实验结果及分析
采用的实验数据为常州地区3块1km*1km的规则格网地形数据,栅格精度为1m,分别设置阈值Ct=1与Ct=0.985进行简化实验。
Ct=1,则最大法向量夹角为0°,即简化时将共面的区域聚合为由4个项点表示的一个区域,与原地形相比无失真。
Ct=0.985,则最大法向量夹角为10°,即聚合区域的面片间夹角均不小于170°。图3列出了其中一块地形数据,数据简化前与用该算法简化后的格网对比。

图3 简化前后的格网对比
由图3(b)可以直观地发现,简化后地形平坦的区域,用较少的数据表示,地形起伏变化大的区域,用较多的数据表示,呈现出多级精度的特点。表1给出了对3块地形数据简化的相应实验数据,其中简化后顶点数包括原地形数据中左侧及下侧条状区域小于初始分块区域大小的栅格点。可以看出对这3块地形数据,即使是不失真的简化,顶点简化率仍高达85%以上。其中主要原因在于这3块地形数据相对平坦,最高海拔12m,最低海拔1m,且精度很高,1m分辨率,因此数据冗余量大,简化效果好;另一原因在于算法本身通过递归过程实现了不同分块大小的区域聚合,最大聚合区域为32*32,最小聚合区域为4*4。对于山区地带地形起伏变化大的数据,适当调整阈值Ct,也可以取得较好的简化效果。

表1 实验数据
3 结束语
对于高精度、大范围海量地形数据快速三维可视化的研究一直是众多研究者关注的问题,目前的研究热点是动态细节层次模型[4-5](Level of Detail,LOD)。本算法与之相比,优势体现在一是数据结构简单、存储量小、易于实现;二是精度可控,对于DEM映射DOM纹理的应用还可以有效保留地形纹理坐标;三是更适用于地形数据的预处理,将三维地形动态绘制的压力部分转移。同时,本算法也存在一定的局限性,即仅限于规则栅格数据的简化与三维绘制,不适用于TIN结构的地形。从总体来说,本算法对于地形快速绘制有一定的实用性。
[1]ROSSIGNAC J,BORREL P.Multi-resolution 3D Approximations for Rendering Complex Scenes[C]//In B.Falcidieno and T.Kunii,editors,Modeling in Computer Graphics:Methods and Applications,1993:455-465.
[2]KALVIN A,TAYLOR R.Superfaces:PolygonalMesh Simplification with Bounded Error[J].IEEE Computer Graphics and Application,1996,16(3):64-77.
[3]ZHU Yuanchen.Uniform RemeshingwithanAdaptive Domain:A New Scheme for View-dependent Level-of-Detail rendering of Meshes[J].IEEE Transactions on visualization and computer graphics.2005,11(3):306-316.
[4]李建军,李俊山.基于特征的三维模型简化算法研究[J].系统仿真学报,2007,19(11):2434-2436.
[5]朱军,龚建华.大规模地形实时绘制算法[J].地理与地理信息科学,2005,21(2):24-27.

