基于公共特征点的三维测量数据拼接方法*

胡 巍,莫建文,王小兵,程 乔

(桂林电子科技大学 信息与通信学院,广西 桂林 541004)

三维视觉测量技术的主要任务是由二维灰度图像求得目标物体的空间三维坐标。目前，关于三维测量的方法有很多，常用的三维测量技术被分为被动式和主动式两大类，前者物体的照明由物体周围的背景光来提供，如双目立体视觉等;后者使用一个专门的光源对被测物体进行照明，如结构光法、莫尔条纹法等。其中，双目立体视觉测量技术结构简单，通过适当的标定方法和立体视觉匹配算法，可以得到较高的测量精度[1]。但是对于大型物体或是回转体的测量，由于双目立体视觉的视场比较小，无法一次完成对被测物体的表面测量，因此需要对被测物体进行分块测量，然后将测量数据拼接融合到一起，组合成完整的三维数据模型，即三维数据拼接。

目前，三维数据拼接方法有精密仪器定位法[2]、双经纬仪法[3]、ICP算法[4]、物体表面贴标志点法[5]等，但这些方法都存在着一些问题：精密仪器价格昂贵,双经纬仪受环境限制难以合理布置,ICP算法复杂、效率低而且精度不高,贴标志点的方法不适合软质和易损伤的被测物。本文采用了一种基于公共特征点的拼接方法，其基本思想是：首先对各个子区域进行单独测量，然后利用重合区域的公共特征点进行连接从而获得整体的测量数据。本文在介绍立体视觉测量系统的基本原理的基础上，重点阐述了三维拼接方法的原理及实现。

1 双目立体视觉测量系统的基本原理

用C1与C2两个摄像机观测空间点P,如图1所示，设它在 2个摄像机C1与C2上的图像点p1与p2已经从2幅图像中分别检测出来，即已知p1与p2为空间同一点P的对应点。空间点P既位于 o1p1上,又位于o2p2上，因此P点是o1p1与o2p2两条直线的交点，即它的三维空间位置是唯一确定的。

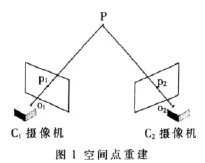
设C1与C2摄像机已标定，它们的投影矩阵分别为M1与 M2。匹配点对用齐次坐标表示为p1=(u1,v1,1)T和 p2=(u2,v2,1)T，对应的空间点齐次三维坐标为P=(x,y,z,1)T。由二维图像点与三维空间点之间的映射关系，可以得到[6]：

其中，k1、k2为比例系数。

将(1)式展开：

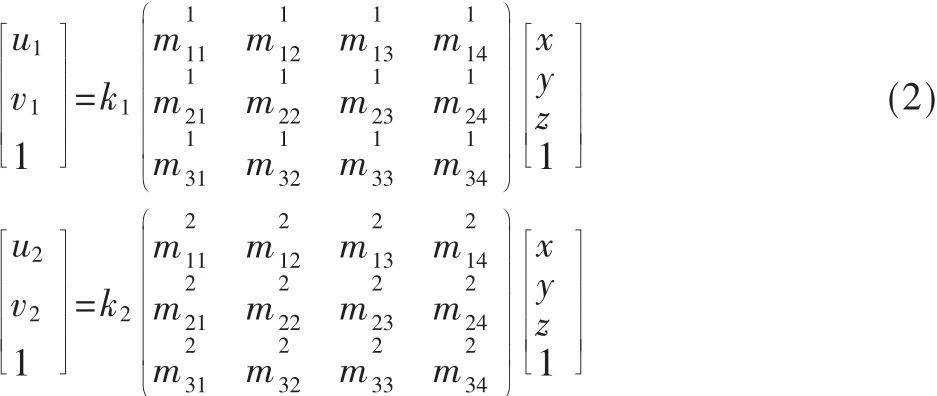
消去(2)式中 k1、k2得到关于x,y,z的4个线性方程：

理论上，联立的方程组必定有唯一解，但实际应用中，由于误差的影响，可能没有确定的解，因此可应用最小二乘法求出P点的三维坐标。从几何关系角度讲，表示的是空间两条直线求交点，由于一些外界的因素使得这两条直线不相交，而是成为异面直线，因此求得的最小二乘意义上的解就是两条异面直线间的最短距离所在线段的中点。

2 基于公共特征点的三维拼接方法

三维测量数据的拼接关键在于如何求出空间之间的变换矩阵。对于大型物体或回转体的视觉测量，可以先把被测物体的表面划分为若干个子区域，并且确保相邻的子区域含有公共区域，然后采用双目立体视觉测量系统对这些子区域分别进行拍摄测量，得到子区域上特征点的三维坐标。再利用重合区域内的若干个公共特征点 (出于对精度和速度方面的考虑，通常选择4～6个点），计算相邻子区域的空间变换矩阵，将各个区域测量的坐标值统一到一个坐标系下，如图2所示。

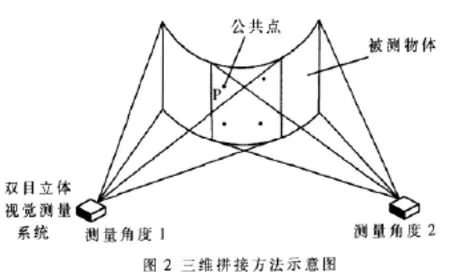
设测量角度1的参考坐标系记为A,测量角度2的参考坐标系记为B，P点在坐标系A和B中的坐标分别为(x1,y1,z1)与(x2,y2,z2)，B到 A的旋转正交矩阵为R，平移向量为 t=(tx,ty,tz)T。

[7]中，变换矩阵求解时，将坐标变换关系表示为∶

其中，W21为坐标系B到坐标系A的变换矩阵。变换矩阵W21含有12个未知量,采用多点的最小二乘拟合法进行平差，如采用4个或4个以上的点，把(4)写成为∶

式中,X1和X2包括两坐标系下4个或4个以上点的齐次坐标，则矩阵W21的解为∶

采用最小二乘拟合，通过三维空间中的多个点求得转换矩阵，计算方法简单，但缺点在于当选取的公共特征点个数较少的时候,计算出的转换矩阵误差较大，拼接效果不理想。

在实际应用中，由于像面点的提取误差，对应点对的位置误差等，由线性方程解得的R矩阵并不满足正交约束条件，因此R的求解要充分利用旋转矩阵的正交条件。但考虑到解非线性方程，计算量较大，引入计算误差。

为此，本文采用Rodrigues参数表示变换矩阵的方法[5,8]。Rodrigues参数是1840年法国数学家Rodrigues提出的用于描述刚体定点转动的姿态描述，它既是姿态描述的最小实现，同时计算效率又很高。设一个具有固定点o的刚体绕单位矢量n转动，刚体上有一定点矢量r1，绕n轴转动θ角至r2的位置，设Rodrigues参数为H=[hxhyhz]T，定义如下：

由Rodrigues参数给出的姿态矩阵为∶

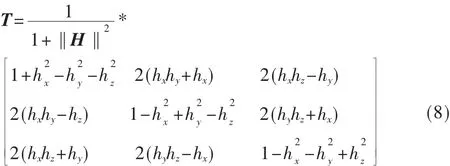
其中,||H||为Rodrigues参数的范数。

它的引入使得转换矩阵的求解过程主要是一些低阶向量和矩阵的代数运算，从而简化了运算，并且当选取的公共特征点较少的时候，也具有较高的精度。

首先，将坐标变换关系表示为∶

设坐标系B相对于坐标系A的Rodrigues参数为H=[hxhyhz]T，则旋转矩阵R可表示为∶

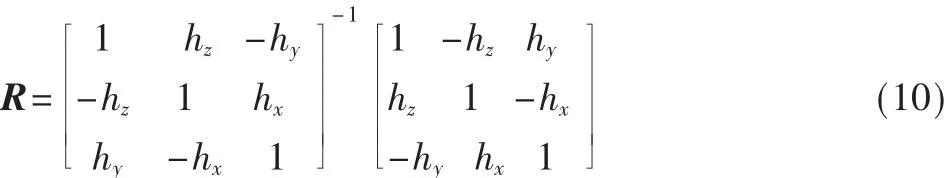
将式(10)代入(9)，可得：

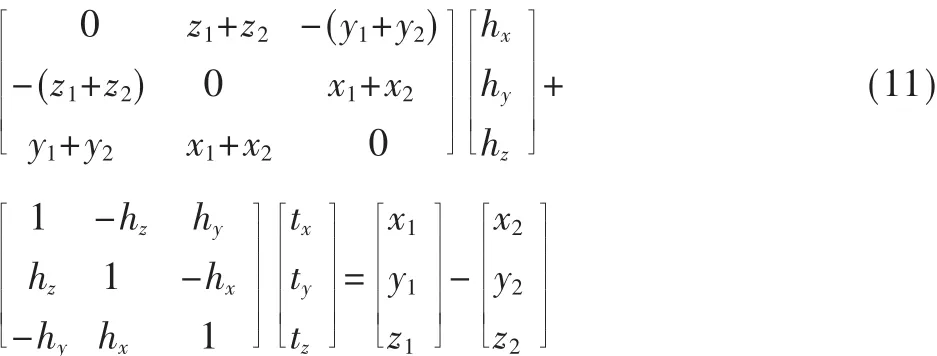
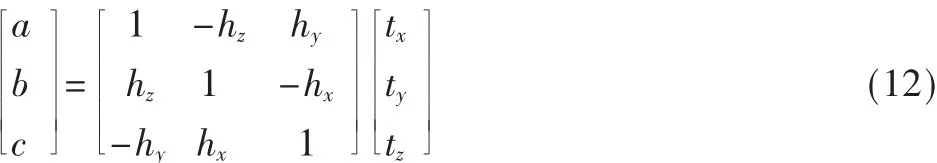
整理上式得：

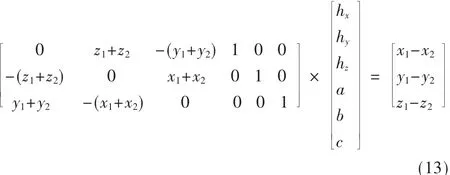
简记为QX=N，在重合区域上选取 k(k≥3)个公共特征点，可以得到如下的方程组：

用最小二乘法求解，则可得到Rodrigues参数以及引入的辅助参数。根据式(10)可求得旋转矩阵R,根据式(12)可求得平移向量t。

3 三维拼接方法的实现

本文用一个盒子作为测试对象，采用双目立体视觉测量系统从两个不同角度对盒子的正面和背面分别进行了拍摄，图像大小为2 304像素×1 728像素。设测量角度1的参考坐标系为A，测量角度2的参考坐标系为B。由于只要测量出盒子的8个顶点便可以勾勒出盒子的外形，因此只把8个顶点作为特征点进行了测量。如图3、图4所示，对应的顶点用0～7依次分别标示出。

实验中，以 2、3、4、5为顶点的侧面为公共区，因此将2、3、4、5作为公共特征点。以上 4个点将用于求解转换矩阵。

首先用双目立体视觉测量系统分别测量出角度1和角度2下特征点的三维坐标值，如表1和表2所示。

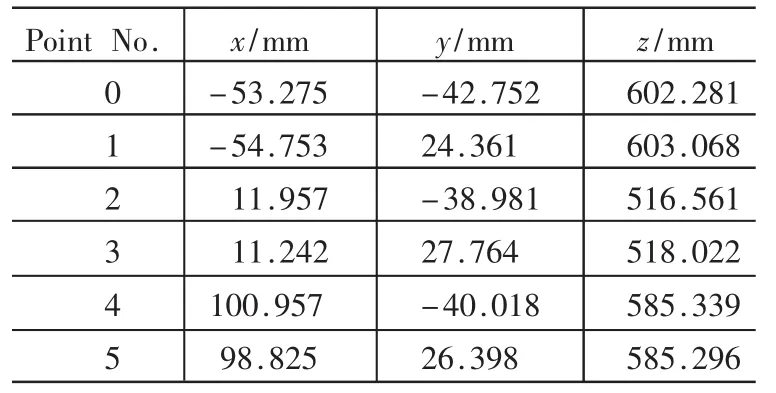
表1 角度1下特征点的三维坐标值

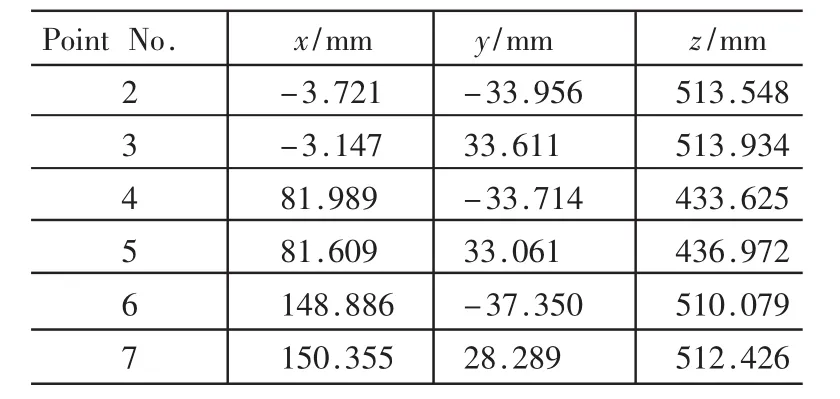
表2 角度2下特征点的三维坐标值

表3 测量误差

采用参考文献[7]中的方法，求得的变换矩阵为∶

通过变换矩阵W21就可以把 B坐标系中6、7两点的三维坐标转换到A坐标系中∶点6(116.789,-45.530,704.775),点7(116.577,19.485,708.524)。为了验证测量出的三维坐标是否正确，通过OpenGL编程将A坐标中的所有空间点进行了显示，如图5所示。

苏楠之所以再次问这个问题，只是想从杨小水嘴里得到确认。明摆着，杨小水没有这样的表姐，有也不可能同时嫁给李石磨，不可能恰好也有过两个小孩，不可能恰好也叫李峤汝、李碧汝。

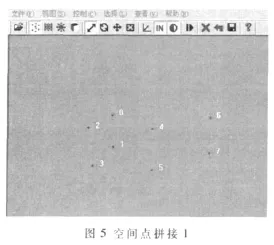
由图5可见，6、7点的位置与实际位置偏差较大，拼接效果不理想。

下面采用本文的拼接算法,首先求解出6个参数值：

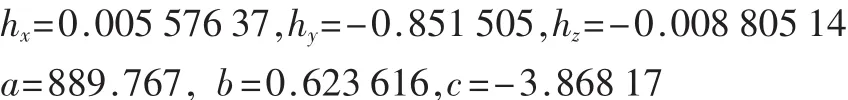
因此，可以求得：

通过R和t就可以把B坐标系中6、7两点的三维坐标转换到 A 坐标系中：点 6（37.675，-44.920，664.610），点 7（35.901，20.693，667.429）,空间点显示如图6 所示。

由图6可见，6、7点的位置与实际位置相符，拼接效果较理想。为了进一步验证此方法测量出的三维坐标的可靠性,用直尺测量出盒子顶点之间的真实距离，并将其与用三维坐标计算出的点间距离作比较，结果如表3所示。从试验结果来看，尺测量值与计算值基本吻合，说明采用此方法能够较好地实现测量数据的拼接。

通过以上理论分析和实验验证，不难看出，利用本文的三维拼接方法可以有效地解决双目立体视觉测量系统视场比较小的问题，并且不涉及复杂的数据处理，稳定性好。该方法适合于具有3个或者3个以上公共特征点对的测量数据拼接，操作简单，精度高，非常适合于实际应用。

参考文献

[1]王锋,吕乃光,韩建栋,等.基于双目视觉跟踪的三维拼接技术[J].北京机械工业学院学报,2008,23(4)：10-12.

[2]龙玺,钟约先,李仁举.结构光三维扫描测量的三维拼接技术[J].清华大学学报,2002,42(4)∶477-480.

[3]周富强,张广军,江洁,等.现场双经纬仪三维坐标测量系统[J].机械工程学报,2004,40(1)∶165-169.

[4]戴静兰,陈志杨,叶修梓.ICP算法在点云配准中的应用[J].中 国 图 象 图 形 学 报，2007,12(3)∶517-521.

[5]欧阳祥波,宗志坚,熊会元.基于标志点的测量数据自动拼接方法[J].中国图象图形学报,2008,13(2)∶298-301.

[6]陈胜勇,刘盛.基于OpenCV的计算机视觉技术实现[M].北京∶科学出版社,2008.

[7]邓文怡,桑新柱,董明利,等.三维拼接在大尺寸视觉测量中的应用[J].光电子·激光,2002,13(11)∶1145-1147.

[8]周江华,苗育红,王明海.姿态运动的Rodrigues参数描 述 [J].宇 航 学 报,2004,25(5)∶514-519.