天津海积软土蠕变特性试验研究

张静娴，杨爱武，张 彦，辛 蕊

(天津城市建设学院a. 土木工程系；b. 天津市软土特性与工程环境重点实验室，天津 300384)

天津海积软土蠕变特性试验研究

张静娴a,b，杨爱武a,b，张 彦a,b，辛 蕊a,b

(天津城市建设学院a. 土木工程系；b. 天津市软土特性与工程环境重点实验室，天津 300384)

通过不排水三轴蠕变试验，对天津海积软土的蠕变特性进行了研究，得出了天津海积软土蠕变特性方程．用灰色系统理论建立了蠕变沉降预测模型 GM(1，1)，并利用试验实测数据进行了计算，结果表明：该预测模型具有较好的精度，对指导实际工程进行蠕变沉降预测有积极意义．

海积软土；蠕变；灰色预测

海积软土主要为淤泥质黏土和淤泥质粉质黏土，富含有机质，呈软塑状态，其特性为含水量高、孔隙比大、压缩性高、天然强度低、透水性小，并具有显著的蠕变性．蠕变是指土在应力状态不变的条件下，应变随时间逐渐增长的现象[1]．经典的弹性、塑性理论认为，土在加荷以后立即产生变形，应力状态恒定且不考虑时间因素．然而许多研究资料表明：应力、应变并不是简单代数关系，而包括复杂的随时间变化的规律[2-5]．海积软土地基上的构筑物经常会由于地基土的蠕变而出现沉降过大、承载力不足等问题．因此，研究海积软土的蠕变特性十分必要．

土的蠕变性最早是在1948年由Geuze E.C.W.A和陈宗基提出的．目前，对土的蠕变研究已经有很大进展，国内外学者在蠕变现象和机制、蠕变特性试验以及蠕变本构模型等方面取得了很多研究成果．在土的蠕变特性试验方面，谢宁、孙钧[6]对上海地区饱和软黏土的流变特性进行了试验研究，提出了描述上海软土流变特性的经验本构模型；王常明、肖树芳[7]对上海、珠海、深圳地区的海积软土进行了一维固结蠕变试验，提出了时间效应系数，并对固结蠕变过程中土的微观结构变化进行了研究；陈晓平、白世伟[8]对软土蠕变-固结特性进行了研究，探讨了应力应变模型、蠕变模型和固结模型的耦合机理；王常明等人[9]对营口、上海、珠海的滨海软土进行了三轴蠕变试验研究，提出了描述滨海软土的应力-应变-时间的经验公式．本文在前人研究工作的基础上，选取天津滨海新区临港工业区某场地的海积软土样，通过三轴蠕变试验研究了天津海积软土的蠕变特性，得到了天津海积软土蠕变特性的经验公式；同时用灰色系统理论建立了蠕变沉降预测模型 GM(1，1)，并用蠕变试验数据进行了预测，对该模型进行了验证．

1 试验方案

1.1 土的基本物理特性

试验选取天津滨海新区临港工业区某吹填场地的海积软土，取样深度为 6.6～8.9,m，土样为灰色淤泥质黏土，有些土样中混有贝壳等杂质．本次试验土样的基本物理性质指标见表1．

表1 土样基本物理性质指标

1.2 蠕变试验方案

本次蠕变试验采用的仪器是由SJ-1A三轴仪改装而成的三轴蠕变仪．将土样置于一定围压下，沿竖向加载框及其下的加压系统对土样施加轴向荷载，形成偏应力状态，使土样产生蠕变变形．由百分表测读土样在一定荷载下随时间的增长而产生的轴向变形．

蠕变试验的加载方式有分别加载和分级加载两种．分别加载就是对同一种土样，在相同仪器和相同的试验条件下，进行不同应力水平下的蠕变试验．从理论上来说，分别加载蠕变试验更符合蠕变试验的要求，能得到蠕变全过程的变化曲线[10]．本试验采用分别加载不排水三轴蠕变试验．试样直径 61.8,mm、高度 150,mm．根据实验目的和现场实际情况，此次试验分为四组，均施加围压150.0,kPa．每组制作 4个土样，分别对1#～4#试样施加垂直向荷载 12.5，25.0，37.5，50.0,kPa．各组蠕变试验持续时间为：第一组1,d，第二组 3,d，第三组 5,d，第四组 7,d．

2 蠕变试验成果及分析

2.1 蠕变曲线特征

图 1为本次试验得到的蠕变持续时间为 1，3，5，7,d的不同垂直向荷载水平下应变-时间曲线图．从图1中可知：对于同一组土，随着应力水平的增加，土体瞬时应变有显著提高；在低应力水平下，应变随时间逐渐趋于稳定值；在高应力水平下，应变随时间稳定增长，土体表现出流动性；当应力达到土体屈服值时，土体快速流动破坏．对于不同组土，在同一应力水平下，其瞬时阶段的应变量不仅受垂直向荷载水平影响，也受土的组成、结构及应力历史等特性的影响；图 1中，在低应力水平下(垂直向荷载 12.5 kPa)，土样的瞬时应变主要受荷载水平的影响，四组土瞬时应变量相差不大；随着应力水平的提高，荷载水平对土体瞬时应变量的影响减小，在较高应力水平下(垂直向荷载 37.5 kPa)，四组土瞬时应变量相差较大，表明在高应力水平土体瞬时应变量受土体土的组成、结构及应力历史等特性的影响较大．

从图1中可以得出，海积软土蠕变变形为四个阶段：①瞬时阶段．该阶段持续时间一般为加载后 0～0.5,h，应变不断发展，应变曲线近似于直线，该阶段变形量在低应力水平时(垂直向荷载 12.5，25.0,kPa)达到总变形的80%～85%，在较高应力水平下(垂直向荷载 37.5,kPa)达到总变形的70%～75%；②不稳定流动阶段．该阶段持续时间随着应力水平的提高有明显增长，在较低应力水平下，该阶段持续时间约为10,h，在较高应力水平下，该阶段持续时间约为 3,d；应变不断发展，应变速率逐渐减小，该阶段应变曲线近似弧线，应变速率随着应力水平的提高有明显增加；③稳定流动阶段．该阶段应变曲线近似直线．在低应力水平下(垂直向荷载 12.5，25.0,kPa)，蠕变具有衰减特征，应变速率逐渐为 0；在较高应力水平下(垂直向荷载 37.5,kPa)，应变以等速稳定增加，土体表现出明显的蠕变特性；④破坏阶段．当应力水平达到土体屈服值时，土体由第一阶段直接进入第四阶段，土体迅速破坏．由以上分析可知：天津海积软土不排水长期强度低于50.0,kPa．

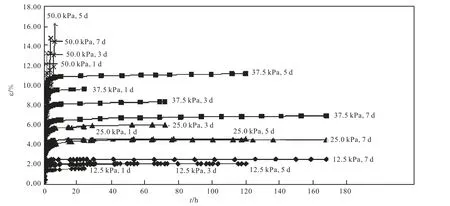
图1 蠕变试验应变-时间曲线

2.2 平均应变速度-时间曲线

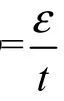
式中：A为比例常数；1t，1ω为常数值．由式(1)可得

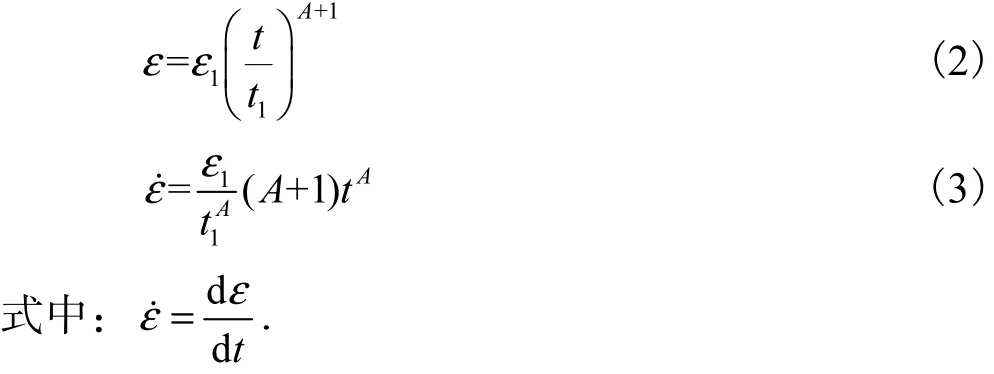
由式(3)可得到天津海积软土的蠕变特性经验公式

根据图2可以计算得到天津海积软土不排水蠕变比例常数A为-0.992，式(2)、式(3)可写为

式(5)、式(6)为此次试验得到的天津海积软土蠕变特性方程，其中1ε为1t时刻的应变量．由式(5)、(6)可知：式(4)中B具有丰富的含义，其大小不仅受荷载水平影响，还反映了土的组成、结构和应力历史等特性对蠕变速率的影响，式(4)中A控制着应变速率随时间减小的速度．由以上分析可以得知，海积软土受到一定荷载作用后的瞬时应变速率与荷载水平、土的组成、结构和应力历史等特性有关，蠕变过程中的应变速率与时间有关，天津海积软土蠕变呈应变速率衰减型，应变-时间关系呈幂指数型．

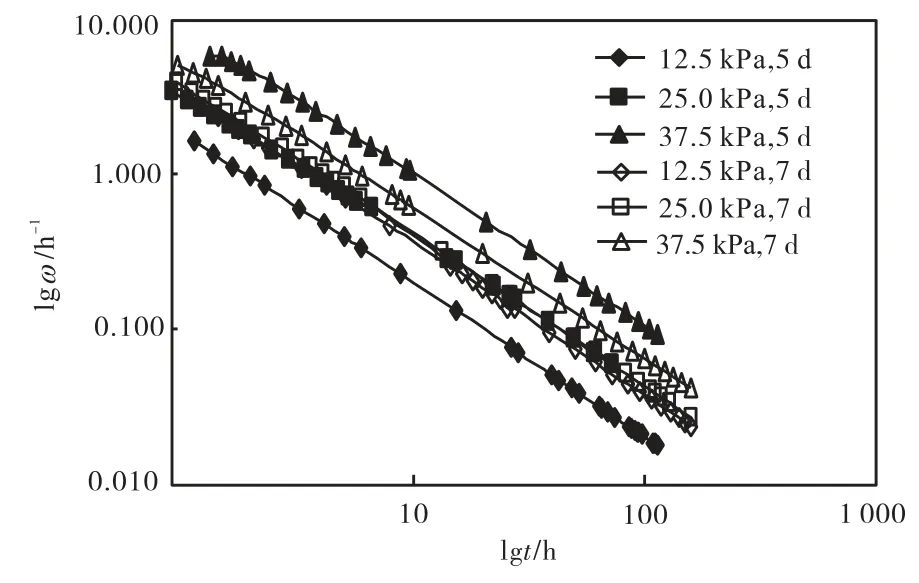
图2 蠕变试验lgω -lgt曲线

3 蠕变沉降预测模型GM(1，1)

由于海积软土具有显著的蠕变性，所以在海积软土地基上进行建设时，为防止建筑物或构筑物的开裂和损坏，保证正常使用，要对未来沉降进行早期预报，从而为有效地治理沉降提供依据．影响海积软土蠕变沉降的因素很多，如土的组成、荷载分布、应力历史等，这些因素之间关系复杂，有些甚至难以精确描述．因此，可以通过灰色系统理论方法，对蠕变沉降原始数据进行处理，建立灰色预测模型，以分析蠕变沉降的发展变化．本文根据灰色系统理论建立蠕变沉降预测模型 GM(1，1)，并用此次蠕变试验数据进行了实例计算．

3.1 灰色预测模型GM(1，1)

灰色系统由我国邓聚龙教授在1982年创立并发展起来．以“部分信息已知，部分信息未知”的“小样本、贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行规律的正确描述和有效控制[11]．灰色模型(gray model，简称 GM)的主要任务是根据系统的行为特征数据，找出因素本身或之间的数学关系，从而了解系统的动态和发展趋势．较为常用的灰色模型为预测模型 GM(n，1)，即拥有一个 n阶导数的灰色系统模型，该变量就是灰色系统中的主因素．当n越大，计算也就越复杂，精度也不一定高[]12．当n=1时，即为计算简单的预测模型GM(1，1)．建立蠕变沉降预测模型GM(1，1)的方法如下．

对蠕变沉降原始数据记为

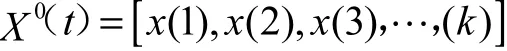
其中：x(1),x(2),x(3),…,x( k)为沉降时间为1，2，3，…，kd时的蠕变沉降量．

为了减少原始数据的随机性和波动性，对0X进行1-AGO(一次累加)序列，得到数据列

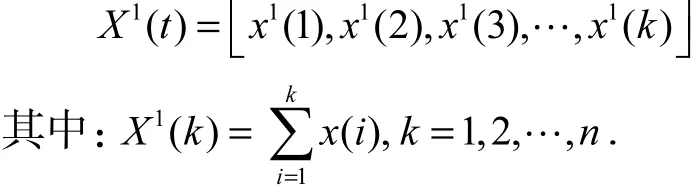
按照灰色系统理论，应满足

将上述微分方程的常微分项差分

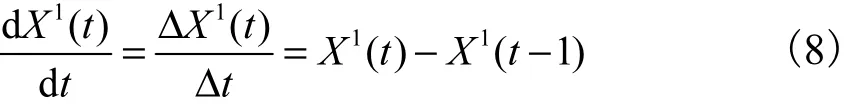
利用最小二乘法对灰色参数a,b进行拟合

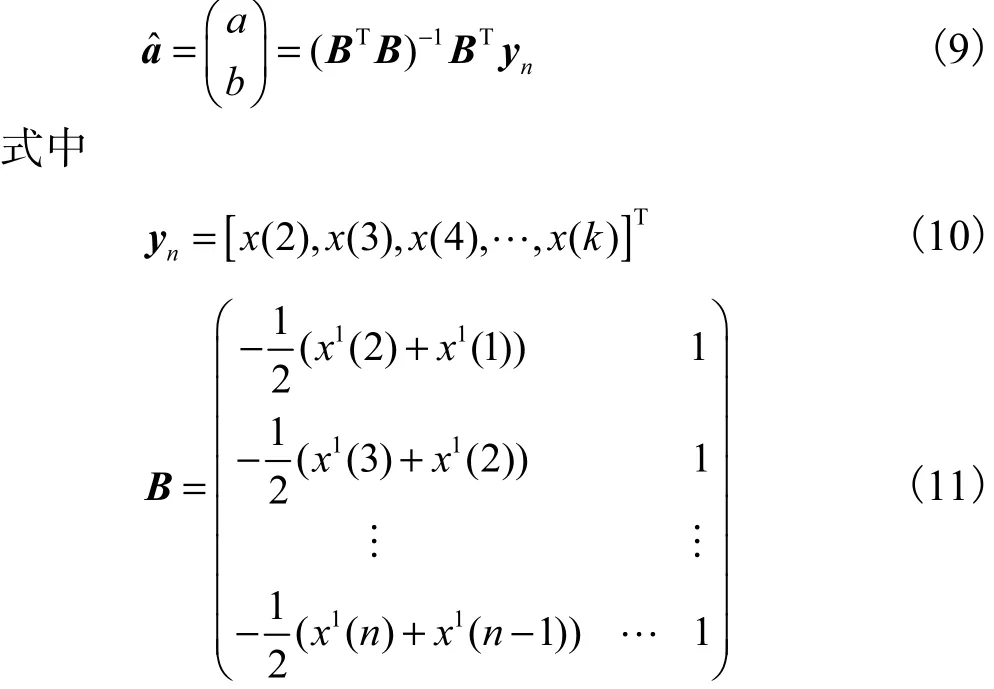
把估计值 a,b代入方程解中，即得到该系统的相应函数

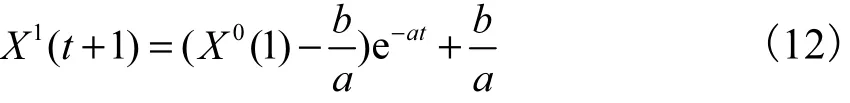
式(12)即为蠕变沉降灰色预测模型．经过 1-AGO的一次累减处理，即可得到不同时刻的预测蠕变沉降量

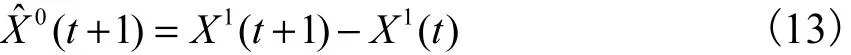
当 t = 1 ,2,… , k时，由式(13)得出的是拟合值；当t≥ k时，X1(t + 1 )为预测值．

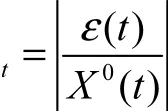
3.2 计算实例

以蠕变持续时间为 7,d、垂直荷载为 37.5,kPa的蠕变沉降数据来建立蠕变沉降模型．蠕变沉降原始数据如下

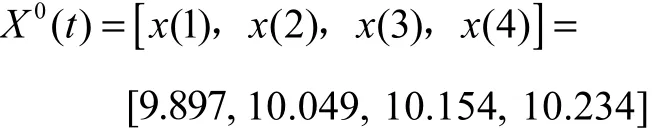
其中：()x t为td时的沉降量， mm．

按式(7)至式(13)计算得到蠕变沉降模型为

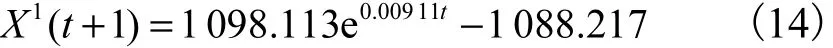
由式(14)可计算得到该模型的拟合值和预测值(见表 2)．由表 2可知：在 5，6，7,d，预测沉降量与实际沉降量相差不超过 0.11,mm，平均相对误差为0.611%，说明该模型能较好地对蠕变沉降曲线进行拟合，模型具有较高的精度．表 2还给出了时间为 30，60,d的预测蠕变沉降量，表明该模型能进行中短期的蠕变沉降预测．由以上分析可知，蠕变沉降预测模型GM(1，1)显示了较好的精度，表明该模型可应用于蠕变沉降预测计算．该模型应用少量的数据即可进行较准确的中短期预测．在进行长期沉降预测时，可根据实测数据置入最新信息、去掉最老信息，建立新模型以提高计算精度．该模型对数据分布及要求没有限制，计算较简便，能对实际工程起到指导意义．

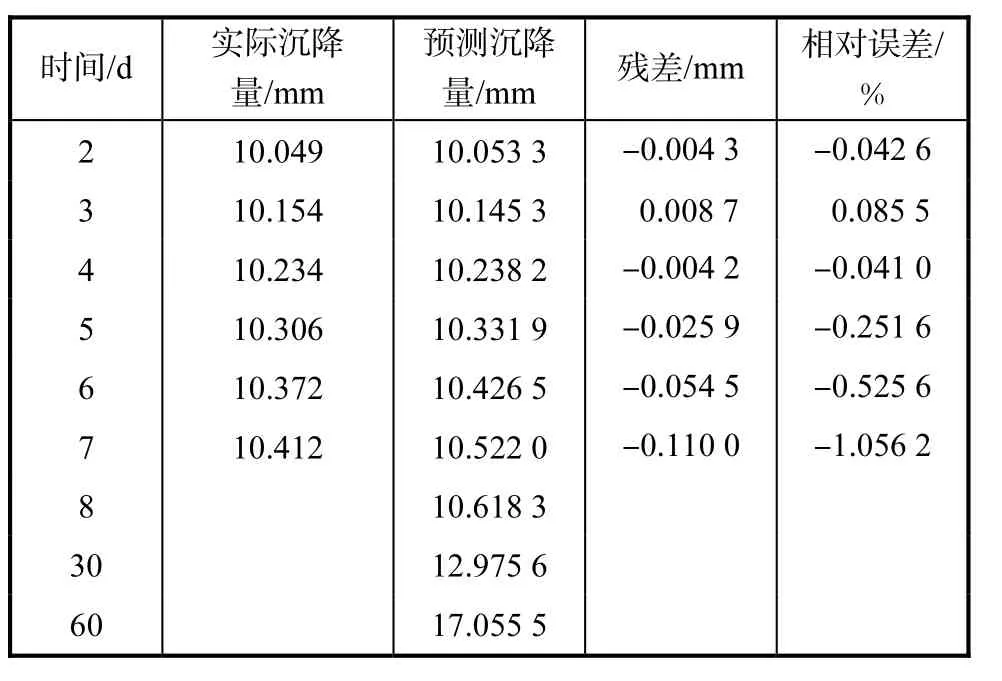
表2 误差检验表

4 结 论

(1)天津海积软土具有较明显的蠕变特性．根据分别加载三轴蠕变试验结果，其不排水条件下的长期强度低于 50.0,kPa．天津海积软土蠕变为三个阶段：瞬时阶段、不稳定流动阶段、稳定流动阶段．一般文献中描述的加速蠕变阶段在本试验中没有出现．

(2)根据试验结果得出了天津海积软土蠕变特性的经验公式．天津海积软土蠕变瞬时应变速率与荷载水平有关，蠕变过程中的应变速率只与时间有关，天津海积软土蠕变呈应变速率衰减型，应变-时间关系呈幂指数型．

(3)用灰色系统理论建立了蠕变沉降预测模型．根据试验数据对该模型进行了验证，结果表明预测值与实际值误差很小，说明该模型具有较高的精度．利用该模型进行蠕变沉降预测具有所需观测资料少、对数据分布及要求没有限制、计算简单等优点，可应用于在实际工程中进行蠕变沉降预测的计算．

［1］李广信. 高等土力学[M]. 北京：清华大学出版社，2004：54.

［2］陈宗基. 固结及次时间效应的单向问题[J]. 土木工程学报，1958，5(1)：1-10.

［3］侍 倩. 饱和软粘土蠕变特性试验研究[J]. 土工基础，1998，12(3)：40-44.

［4］李西斌. 软土流变固结理论与试验研究[D]. 杭州：浙江大学，2005.

［5］刘汉龙，扈胜霞，Ali Hassan. 真空-堆载预压作用下软土蠕变特性试验研究[J]. 岩土力学，2008，29(1)：6-12.

［6］谢 宁，孙 均. 上海地区饱和软粘土流变特性[J].同济大学学报，1996，24(3)：232-237.

［7］王常明，肖树芳. 海积软土固结蠕变的实效本质研究[J]. 工程地质学报，2000，8(增刊)：334-336.

［8］陈晓平，白世伟. 软土蠕变-固结特性及计算模型研究[J]. 岩石力学与工程学报，2003，22(5)：728-734.

［9］王常明，王 清. 张淑华. 滨海软土蠕变特性及蠕变模型[J]. 岩石力学与工程学报，2004，23(2)：227-230.

［10］艾志雄，边秋璞，赵克全. 岩土蠕变试验及应用简介[J]. 三峡大学学报：自然科学版，2006，28(6)：518-521.

［11］郭文杰. 基于灰色系统理论的深基坑边坡稳定性研究[D]. 武汉：华中科技大学，2008.

［12］胡 冬，张小平. 基于灰色系统理论的基坑变形预测研究[J]. 地下空间与工程学报，2009，5(1)：74-78.

［13］刘思峰，党耀国，方志耕. 灰色系统理论及其应用[M].北京：科学出版社，2004：11，125-166.

［14］谢定义，姚仰平，党发宁. 高等土力学[M]. 北京：高等教育出版社，2008：185-195.

［15］孙更生，郑大同. 软土地基与地下工程[M]. 北京：中国建筑工业出版社，1984：27-63.

Experimental Study on Creep Characteristics of Tianjin Marine Soft Soil

ZHANG Jing-xiana,b，YANG Ai-wua,b，ZHANG Yana,b，XIN Ruia,b
(a. Department of Civil Engineering；b. Tianjin Key Laboratory of Soft Soil Characteristic and Engineering Environment，TIUC，Tianjin 300384，China)

Through a series of triaxial creep tests, this paper studies the creep characteristics of Tianjin marine soft soil, and then proposes the empirical equation for the creep characteristics. It establishes the grey prediction model GM(1,1) for creep subsidence using grey system theory, and then it examines the model using the data of creep tests.The results show that the prediction model has a rather better accuracy and precision. This model will benefit the creep subsidence prediction of construction.

marine soft soil；creep；grey prediction

TU447

A

1006-6853(2010)02-0102-05

2010-01-15；

2010-03-09

张静娴（1983—），女，湖北天门人，天津城市建设学院硕士生.