数字图像相关方法最优散斑尺寸

王志勇，王 磊，郭 伟，沈 珉

(天津大学机械工程学院，天津 300072)

数字图像相关方法(digital image correlation，DIC)是一种成熟的实验力学技术，被广泛应用于位移场和应变场的测量[1]．作为一种测量技术，最重要的是测量精度问题．国内外研究人员对 DIC位移测量精度做了大量研究．根据具体测试条件的不同，DIC的位移测量精度约为 0.01～0.05像素[1]．影响DIC位移测量精度的因素主要包括图像质量、亚像素插值方法、子区内位移模式、光学镜头失真和搜索算法等．Sutton等[2]分析了亚像素插值方法对位移测量精度的影响；Sun等[3]用实验方法分析了图像对比度和聚焦误差对位移测量精度的影响；Schreier等[4]用数值模拟方法分析了子区内位移模式函数对测量精度的影响；陆桦[5]从统计学原理出发，对 DIC的随机误差进行了分析；Saturu[6]和张东升[7]分别研究了光学镜头的镜头畸变对 DIC位移测量精度的影响；潘兵等[8]研究了不同的亚像素匹配方法对位移测量精度的影响；Vendroux等[9]研究了相关系数Hessian矩阵的不同算法对测量精度的影响；笔者[10]曾研究随机噪声对位移测量误差的影响．

在 DIC实验过程中，为了取得较高的测量精度需要在试件表面制作人工散斑．人工散斑大都是通过在试件表面喷洒油漆制作而得，不同制作方法得到的散斑点尺寸和形状有很大差异．试件表面的散斑是试件变形信息的载体，其大小和形状对 DIC的测量精度有很重要的影响．笔者建立理论模型与数值实验分析了散斑点尺寸对于 DIC位移测量精度的影响，给出了最优的散斑点尺寸．在此基础上，进一步将最优散斑尺寸转化为最优灰度梯度，建立了以测量精度为目标的散斑图像评价标准．

1 理论模型

DIC方法的位移测量误差可分为系统误差和随机误差 2个部分．系统误差指由亚像素插值方法所导致的位移测量误差；随机误差指由 CCD摄像机暗电流引起的图像灰度波动所导致的位移测量误差．

为了取得亚像素的测量精度，DIC中需要使用插值算法计算亚像素位置上的灰度值．文献[2]指出，大多数插值算法都存在相位误差，所以用 DIC方法得到的位移值中存在一个不可避免的系统误差．该文献同时给出了使用3次Lagrange插值方法时系统误差的表达式

式中errs、k和δ分别为系统误差、归一化波数和亚像素位移．对于周期为 T的正弦波，归一化波数 k＝2/T．由式(1)可知，亚像素位移值和图像信号频率是影响系统误差的 2个关键因素．文献[2]的分析结果表明：对于相同的亚像素位移，信号频率越高系统误差越大；对于单一频率信号，当亚像素位移为±0.25像素时系统误差最大．

DIC方法是以数字图像为基础的，而实际实验中的数字图像一般由 CCD摄像机采集．由于 CCD摄像机在摄像过程会受到暗电流的影响，因此采集到的数字图像中通常包含了随机灰度噪声．这个灰度噪声对于 DIC的位移测量精度有重要影响．本文将由 CCD暗电流引起的位移测量误差称为随机误差．文献[10]给出了此随机误差的表达式

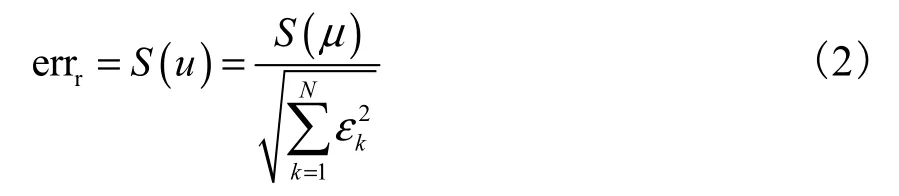
式中 errr、S(u)、S(μ)、N 和 εk分别为随机误差、位移测量值的标准差、灰度噪声的标准差、子区内像素的个数(即子区大小)和子区内第 k个像素与相邻像素之间的灰度梯度．由式(2)可知，相邻像素间灰度梯度与随机误差成反比．灰度梯度越大，随机误差越小；灰度梯度越小，随机误差越大．

图像中的信号频率、散斑尺寸和灰度梯度是3个不同的概念，但三者又有非常紧密的联系．一般来说，信号频率高就意味着散斑尺寸小，相邻像素间的灰度梯度大；信号频率低就意味着散斑尺寸大，相邻像素间的灰度梯度小．由式(1)可知，为了降低系统误差，应使用频率较低的图像．但较低的频率同时意味着较大的散斑尺寸和较低的灰度梯度．由式(2)可知，为了降低随机误差，应提高灰度梯度．而较高的灰度梯度意味着较小的散斑尺寸和较高的信号频率．可见，同时减小系统误差和随机误差对图像的要求是矛盾的．因此，应存在一个最优的散斑尺寸使系统误差和随机误差的总和达到最小．

为简便起见，假设图像中散斑点的形貌为正弦波型，如图 1所示．散斑半径和归一化波数之间的关系可表示为

若所采用的图像是8位灰度图像(即图像灰度级为 0～255)，且图像中相邻像素间灰度梯度的均值为ε，那么ε和散斑半径之间的关系可表示为

图1 理论模型中的散斑形貌Fig.1 Shape of speckle spot in theoretical model

测量误差是系统误差和随机误差的总和，将式(3)和式(4)带入到式(1)和式(2)，并将系统误差和随机误差相加可以得到

式中 err为总测量误差．亚像素位移 δ＝0.25像素时所对应的系统误差最大，用这个最大值来表征系统误差．由式(5)可知，散斑半径R、噪声标准差S(μ)和子区大小N是影响总测量误差的3个因素．

另外，相邻像素灰度梯度也可以用来间接表征散斑尺寸．总测量误差可以用相邻像素灰度梯度均值表示为

2 模拟实验

由于第1节的理论模型是针对正弦信号的，所以数值模拟实验也采用正弦型图像作为研究对象．具体实验方法如下．

1)制作原始图像

用下式生成256个灰度级的正弦型图像，图像灰度只在水平方向有变化，在竖直方向没有灰度变化．

式中：u＝0；x和 R的单位为像素．每幅图中半径 R是相同的，以0.5像素为间隔．半径R从2像素变化到10像素，共制作17幅原始图像．

2)制作平移图像

在式(7)中取 u＝0.25，制作与原始图像相对应的半径R从2像素变化到10像素的17幅平移图像．

3)计算系统误差

用 DIC方法计算原始图像和平移图像间的相对位移，再用计算得到的位移值减去 0.25即可得到位移计算的系统误差．计算时子区分别取21×21、31×31和 41×41．由于图像在竖直方向没有灰度变化，因此在计算过程中只计算水平方向的位移．

4)计算随机误差

在原始图像上分别加均值为0，标准差分别为1、2和 3的高斯噪声，计算原始图像和加噪声图像之间的位移场．将计算所得位移场的标准差作为随机误差．

5)计算总测量误差

将系统误差和随机误差相加作为总测量误差．

3 结果与讨论

图 2(a)和(b)分别为用理论模型和模拟实验得到的子区大小为 31×31，灰度噪声标准差分别为 1、2和 3时测量误差随散斑半径的变化曲线．理论模型结果和模拟实验结果基本一致．由图 2可知，随着散斑半径R逐渐增大，总测量误差先骤然减小后缓慢增大．可见，对于不同的噪声都存在一个最优的散斑半径 R0使总测量误差最小．当灰度噪声标准差为 1、2和 3时，根据理论模型可知，最优散斑半径分别为6.4、5.6和 5.0像素．最优散斑半径随着灰度噪声标准差增加而减小．

图2 不同噪声水平下测量误差随散斑半径的变化曲线Fig.2 Variation of measurement error with different speckle radii at different noise levels

图 2中误差曲线的特点非常明显．当 R＜R0时，随着 R减小，测量误差增加地非常快；而当 R＞R0时，随着R增大，测量误差增加缓慢，尤其当噪声较小时，测量误差随 R的增加速度更慢．因此，只要略微降低对测量精度的要求就可以换取一个较宽的最优散斑半径区间，这是非常有意义的，这样就可以扩大最优散斑图像的选择范围．若误差最小值记为 err0，将在误差区间[err0，err0+Δ]对应的半径区间称为最优半径区间．目前，普遍接受 DIC方法的位移测量精度最高为0.01像素，取Δ＝0.01×5%＝0.000 5．根据这个定义，子区大小为 31×31，噪声标准差为 1、2和 3时对应的最优半径区间分别为[4.4，11.6]、[4.0，8.6]和[4.0，7.2]．显然，低噪声图像对应的最优半径区间相对较宽．

图 3(a)和(b)分别为用理论模型和模拟实验得到的灰度噪声标准差为 2，子区大小分别为 21×21、31×31和 41×41时测量误差随散斑半径的变化曲线．理论模型结果与模拟实验结果基本一致．由图 3可知，散斑半径相同时，选用的子区越大测量误差越小．根据理论模型，与这3个子区尺寸相对应的最优半径分别为5.0、5.6和5.8像素，最优半径随着子区地增大而增大．与图 2的结果类似，在图 3中，当 R＞R0时，随着 R增大，测量误差增加地非常慢．特别是当子区较大时，测量误差增加的速度更慢．与前述相同的误差条件下，21×21、31×31 和 41×41 三种子区对应的最优半径区间分别为[4.0，7.4]、[4.0，8.6]与[4.2，9.6]．可见，大子区对应的最优半径区间相对较宽．

图3 对于不同的子区测量误差随散斑半径的变化曲线Fig.3 Variation of measurement error with different Fig.3 speckle radii for different subsets

如前所述，通过式(4)，散斑半径尺寸也可以间接地用相邻像素灰度梯度来表示．最优散斑半径用式(4)很容易转化为最优梯度，最优散斑半径区间可以相应地转化为最优梯度区间．例如当灰度噪声标准差为2，子区大小为31×31时最优散斑半径为5.6像素，最优散斑半径区间为[4.0，8.6]，用式(4)可计算相应的最优梯度为45.5，相应的最优梯度区间为[30，64]．对于一幅散斑图像而言，各点的梯度是不同的．如果全部点的灰度梯度都在最优梯度区间内，那么就可以认为这幅图是最优的．

在 DIC实验准备阶段，通常可以在试件表面制作多种不同的散斑图．但由于没有客观评价标准，很难确定哪个图可以取得较高的测量精度．本文的研究结果可以为散斑图的选择提供一个客观评价标准．综合前面的分析，这个标准可以表述为：图像中灰度梯度处于最优梯度区间的点越多越好，灰度梯度比最优梯度区间右边界大的点越少越好．

图4所示是2幅散斑图像．其中图4(a)是一幅实际的散斑图像，图 4(b)是利用文献[11]中介绍的方法用程序生成的一幅散斑半径为 3像素的散斑图像．以笔者的经验来说，这 2幅散斑图的斑点大小基本一致，斑点分布均匀，是质量较好的散斑图像．按噪声标准方差为 2，子区大小为 31×31的标准，表 1给出了这 2幅的灰度梯度分布情况．图 4(b)的梯度平均值更接近于最优梯度，在最优梯度区间的点更多，而且没有大于最优梯度右边界的点，所以与图4(a)相比，图4(b)更适合DIC．

图4 2幅散斑图像Fig.4 Two speckle images

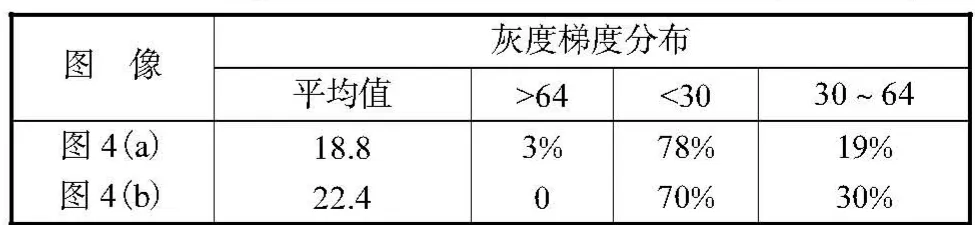
表1 图4中2幅图像的灰度梯度分布Tab.1 Gray gradient distribution of two images in Fig.4

4 结 语

通过综合分析由亚像素插值引起的系统误差和由灰度随机噪声引起的随机误差，建立了计算数字图像相关方法的总测量误差数学模型．对该模型取极小值得到最优的散斑半径．通过适当降低对测量精度的要求建立了最优散斑半径区间的概念．研究结果表明，灰度噪声标准差和计算过程中的子区大小对最优散斑半径和最优散斑半径区间有直接影响．通过将散斑半径转化为灰度梯度，相应地建立了最优梯度和最优梯度区间的概念．在此基础上提出了对散斑图像质量进行客观评价的标准：图像中灰度梯度处于最优梯度区间的点越多越好，灰度梯度比最优梯度区间右边界大的点越少越好．

［1］ Chu T C，Ranson W F，Sutton M A，et al. Applications of digital image correlation techniques to experimental mechanics [J].Exp Mech，1985，25(3)：232-244.

［2］ Schreier H W，Braasch J R，Sutton M A．Systematic errors in digital image correlation caused by intensity interpolation [J].Opt Eng，2000，39(11)：2915-2921.

［3］ Sun Zili，Lyons J S，McNeill S R. Measuring microscopic deformation with digital image correlation [J].Opt Laser Eng，1997，27(4)：409-428.

［4］ Schreier H W，Sutton M A．Systematic errors in digital image correlation due to undermatched subset shape functions [J].Exp Mech，2002，42(3)：303-310.

［5］ Lu Hua．Statistical analysis of the random error in measurements obtained using digital correlation of speckle patterns [C]//Proc of the1993SEM Spring Con On Exp Mech.Michigan，1993：930-937.

［6］ Saturu Yoneyama，Hisao Kikuta．Lens distortion correction for digital image correlation by measuring rigid body displacement [J].Opt Eng，2006，45(2)：023602.

［7］ Zhang Dongsheng．Displacement/strain measurements using an optical microscope and digital image correlation[J].Opt Eng，2006，45(3)：033605.

［8］ Pan Bing，Xie Huimin，Xu Boqin，et al. Performance of sub-pixel registration algorithms in digital image correlation [J].Meas Sci Technol，2006，17(6)：1615-1621.

［9］ Vendroux G，Knauss W G. Submicron deformation field measurements(Ⅱ)：Improved digital image correlation[J].Exp Mech，1998，38(2)：86-92.

［10］ Wang Zhiyong，Li Hongqi，Tong Jingwei，et al. Statistical analysis of the effect of intensity pattern noise on the displacement measurement precision of digital image correlation using self-correlated images [J].Exp Mech，2007，47(5)：701-707.

［11］ 潘 兵. 数字图像相关方法及其在实验力学中的应用[D]. 北京：清华大学航空航天学院，2008.

Pan Bin. Research on Digital Image Correlation with Its Application in Experimental Mechanics[D]. Beijing：School of Aerospace，Tsinghua University，2008(in Chinese)．