图论在农村自来水管网设计中的应用

岳延兵，范 敏

（山西水利职业技术学院，山西 运城 044004）

图论是组合数学的一个分支，也是近几十年来最活跃的数学分支之一，具有以下特点：蕴含了丰富的思想、漂亮的图形和巧妙的证明；涉及的问题多且广泛，问题外表简单朴素，本质上却十分复杂深刻；解决问题的方法千变万化，非常灵活，常常是一种问题一种解法。图论研究的内容非常广泛，如图的连通性、遍历性、图的计数、图的着色、图的极值问题、图的可平面性等。下面具体研究图论在农村自来水管网设计方面的应用。

1 农村自来水管网优化设计指标

农村自来水管网优化设计的指标主要有可靠性、水压水量的保证性和经济性。

1.1 可靠性

可靠性是指在规定的使用状态下、规定的时间内完成预定功能的性能。对农村饮水工程供水管网而言，预定功能是指在正常工作条件下，保证给水栓所需的水量和水压。在工程设计中考虑到可靠性，就有可能减少因故障引起的损失和维修费用。在管网优化设计时，其可靠性应达到在发生事故的情况下，水量和水压不低于规定的限度，而在时间上不超过允许减少水量和降低水压的时间。

1.2 水压水量的保证性

在正常工作时，各个给水栓的水压、水量要达到设计要求，以免水压过高引起水量和能量的浪费，防止下游因水压降低导致水压和水量的不足。

1.3 经济性

在农村饮水供水工程中，经济性是在进行管网优化设计时所要考虑的一个重要指标。管线的费用主要与水管材料、长度和直径等有关，因此，在管网设计时应根据给水栓的布置确定最优的管网布置方案，减小管网的长度;在此基础上，确定管网的最优管径组合，以期达到整个管网的经济性。

以上设计目标除了经济性外，其他方面都不易进行定量评价。如用水量变化和管道损坏等原因使计算流量不同于实际流量，泵站的运行方式、管理水平等也会影响管网设计目标的实现。因此在管网设计中，主要是对管网的布置和管径的选择进行优化，选出最佳方案，尽量达到设计目标。

2 应用图论优化自来水管网布置

在图论中，图是顶点与连接这些点的边的集合，表示为G=（V，E），其中V是顶点的集合，E表示边的集合。在管网的优化布置中，将每个给水栓或配水水源看成是图上的一个顶点，给水栓之间的连接管看作是边，从而形成图。通常以边的长度或造价为边的权重，它与两给水栓之间的连接顺序无关，因此称之为赋权无向图。当图G有n个顶点时，边的数目为n（n-1）/2条，称为无向完全图。如果图G中有两个顶点U和V二者之间存在一条道路，则称U和V是连通的，若图G中任意两顶点连通，则称图是连通的，否则称为非连通的。

连通的没有回路的图称为树。它是图的一种特殊形式，其数据元素（即给水栓的序号）有层次关系，某一层上的元素与上一层的一个元素联结，与下一层的多个元素联结。n个顶点时，只有n-1条边，如多加一条边即形成回路，成为环状网，所以树是无向图中的非完全图，且是极小连通子图。若图G的树包含图G的所有顶点，则称为图G的一棵生成树或支撑树。如果T=（V，E）是G的一个支撑树，则称E中所有边的权之和为支撑树T的权，记为W（T），如果支撑树T的权W（T）是G的所有支撑树的权中最小的，则称T是G的最小生成树。

2.1 最小生成树法

图的最小生成树可采用Kruskal法和Prim法确定。Kruskal法是按权值递增的顺序来构造最小生成树，又称避圈法。先将水源至各给水栓及各给水栓之间按递增顺序排列，再选最短两条线段连接起来，然后由小到大连接各顶点，但不可与已选取的边形成“圈”，如此将所有节点连接起来即可得到最小生成树。Prim法的基本思想是：从某一点开始设为V1，则作S←Vl，然后寻找V/S中的点与S中点距离最短者，设为（Vk，Vi），其中Vk∈S，Vi∈V/S，则将（Vk，Vi）边收入到树T中来，且Vi进入S。依次反复进行，直到n个顶点用n-1条边连接起来为止。

这两种方法都可以找到每个问题的最小解。它们是两种不同的算法，但Prim法回避了必须检验圈的要求，也回避了将所有的边按权值排序，从而节约了时间，提高了速度，因此比Kruskal法更有效。

对于管网的优化布置，仅仅寻求最小生成树并不能实现投资最少的目标。最小生成树仅是管网投资减少的一个因素，它所寻求的是整个管网的总长度最短，即所有顶点之间的最短连接，而不是一点到其余各点之间的最短连接。在管网布置时，假定各个管段的直径是均一的，但当水源位置不同时，各段管径的大小有较大差异，因而对造价的影响较大。通过缩短流量和直径较大的管段长度，同时增加流量较小的直径较小的管道长度，使管网的总投资进一步降低。这一问题可采用最短路径法得以解决。

2.2 最短路径法

在图论中，最短路径法是由荷兰学者Dijkstra提出的，它可用于求解一个顶点到其他所有顶点的最短路径问题。在管网布置中，可用最短路径法求出确定的单一水源至其余各节点均为最短距离的树，从而优化管道布置，节省投资。

最短路径法的基本思想是：从水源V出发，逐步向外探寻最短路，执行过程中，与每个点对应，记录下一个数，或者是从V到该点的最短路的权（记入P），或者是从K到该点的最短路的权的上界（记入T），不断地修改T，并且把某一个T标号的点改变为P标号的点，这样至多经过n-1步，就可求出从K到各点的最短路。

从理论上而言，上述方法可对管网进行优化计算，但在农村自来水工程管网优化设计中，由于其特殊性，在应用时必须考虑其各自工程的特殊情况。

3 算例及讨论

山西省农村饮水任务很重，近几年投入力度不断加大。在这方面也进行了不懈的实践，下面以万荣县农村自来水管网设计为例进行叙述，简化为示意图1。

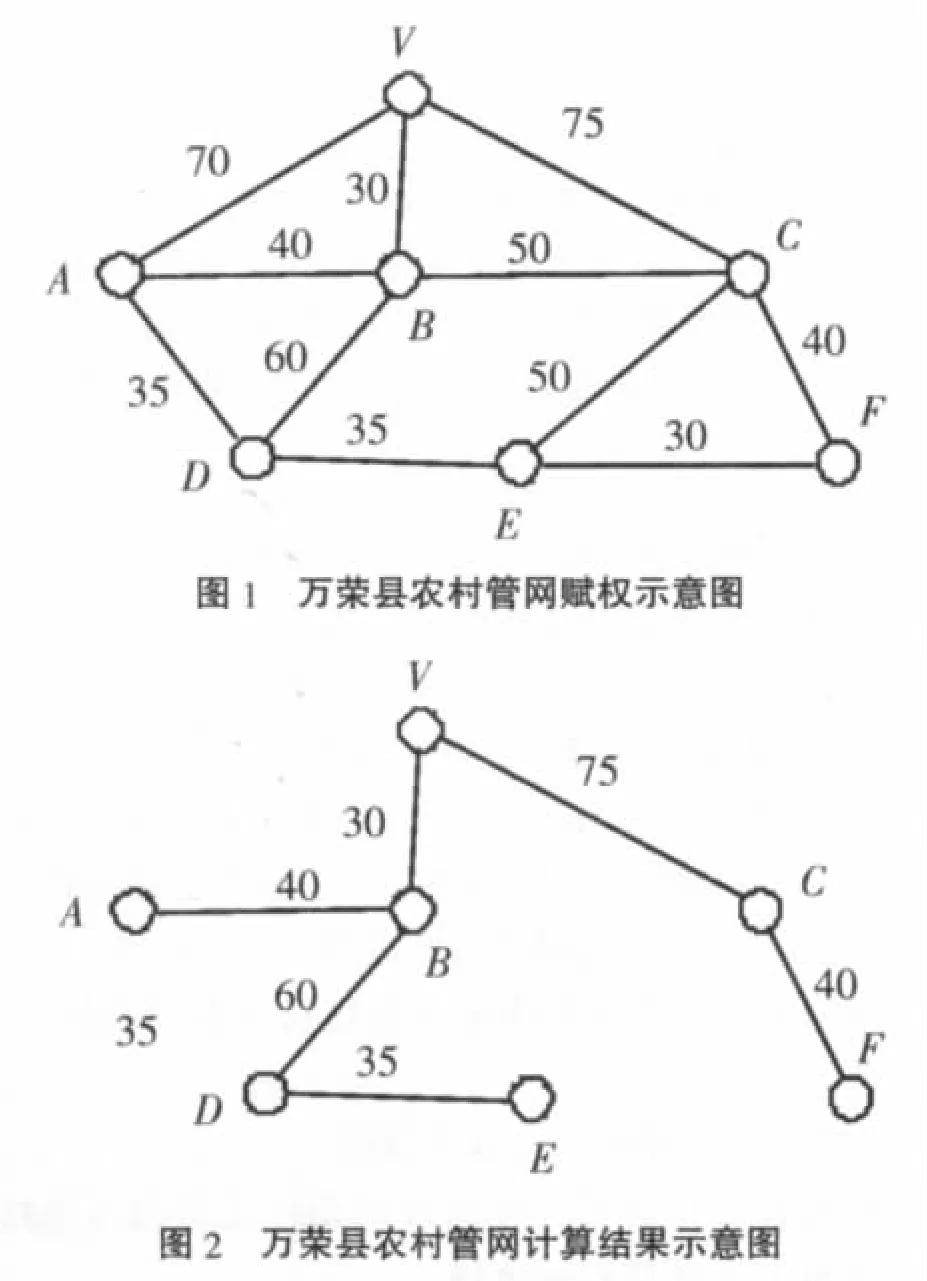
图中V点为水源点，A～F点为用户节点，各点之间距离为节点间权重。计算过程见表1，计算结果见图2。为了便于管网良好运行，取V~B段管径为8cm，V~C和B~D段管径为6cm，B~A，D~E和C~F段管径为4cm。

表1 万荣县农村管网赋权示意图最短路计算表

自来水管网的设计计算经过了从手算到电算，从凭经验设计到优化设计阶段，这一过程是与计算方法和计算工具的发展相适应的。传统方法是凭经验查阅大量表格进行设计的，过程繁琐，计算结果不准确。随着优化理论的发展，自来水管网的优化设计也相应开展起来。在自来水管网优化设计中，特别是针对农村自来水管网分布分散的特点，图论将发挥越来越大的作用。

4 结语

图论是一种对农村自来水管网设计进行有效优化的数学方法，是将复杂的农村自来水管网处理为相应的网络图，并建立相应的数学模型，用原始数据来描述管网结构，输入的数据量少，不易出错，易于计算大型的复杂管网，其计算过程可同时考虑管网附件，如控制阀、加压泵、逆止阀、减压阀等，使计算结果更加符合实际，在农村自来水管网设计中具有很好的应用前景。