楠木人工林树冠体积与叶面积指数预估模型的研究
杜 娟,范志霞,叶顶英,卢昌泰
(四川农业大学都江堰校区,四川 都江堰 611830)
楠木人工林树冠体积与叶面积指数预估模型的研究
杜 娟,范志霞,叶顶英,卢昌泰*
(四川农业大学都江堰校区,四川 都江堰 611830)
摘要:基于楠木(Phoebe zhennan)人工林5块固定标准地25株枝解析数据,进行楠木人工林树冠体积与叶面积指数预估模型研究,研究结果表明:楠木人工林树冠体积和叶面积指数随着林木胸径、树高、冠幅和冠高的增大而增大;在分析树冠体积和叶面积指数与林木变量的基础上,利用SPSS统计软件建立了树冠体积(V)和叶面积指数(LAI)的预估模型:所建立的楠木人工林树冠体积的预估模型为:V= 0.2750L2.253H10.770(L为冠幅,m;H1为冠高,m),叶面积指数的预估模型为:LAI= 0.7845+0.5481H1-0.0288H12+0.0007H13;对预估模型进行检验,结果表明,两个模型的预估精度均大于88%,说明所建模型可以较好地预估楠木人工林树冠体积和叶面积指数。
关键词:楠木人工林;树冠体积;叶面积指数;模型
树冠是树木净第一性生产力的主要来源,直接影响到树木积累有机物的多少,并将影响到树木的健康状况[1]。树冠作为森林生态系统的一个重要组成部分,还将影响到林分下层动植物群落的组成和变化,同时树冠对林分的太阳能分配、养分循环、降雨量分配和保水性等方面都起着重要的作用[2~4]。树木叶面积及其在树冠内的空间分布状况是影响冠层辐射场和光合生产最重要的因子之一,叶面积的大小直接决定了冠层光合叶面积的大小,直接影响林分对光能的截获及利用,进而影响着林分生产力[5]。叶面积指数(1eafarea index,LAI)由英国农业生态学家Watson于20世纪40年代中期提出,经过半个世纪的系统研究,LAI已成为表征植被冠层结构和植物群落生产力的重要指标,是在林冠水平上以及景观尺度上模拟水分蒸发蒸腾损失总量的一个重要指标[6]。
楠木(Phoebe zhennan)作为一种重要的用材及观赏树种[7],目前对其树冠结构和叶面积指数的研究尚未见报道。本文通过对楠木人工林树冠体积与叶面积指数预估模型的研究,为进一步研究楠木林分生长模型及经营模型提供理论基础。
1 研究区概况
楠木人工林实验地位于四川农业大学都江堰实习林场(103° 25′ 42″~103° 47′ E,30° 44′ 54″~31° 22′ 9″N),海拔592 m,年平均无霜期280 d,年平均气温15℃,历年最冷月平均气温4.6℃,最热月平均气温24.4℃;平均年降水量为1 438.0 mm;年平均最大相对湿度80%,最小相对湿度75%;太阳辐射量为370~420 kJ/cm2,历年平均日照时数1 016.9 h;历年平均雷暴日数28 d[8]。本人工林林分为楠木纯林,林下土壤主要是紫色砂叶岩与石灰岩风化而成的山地黄壤,团粒结构,轻壤,土壤润潮,微酸性,pH值6.5~6.8,土层厚度为50~100 cm。
2 研究方法
2.1 样木选取
2008年8-9月,在四川农业大学都江堰校区实习林场不同林分条件的楠木人工林中设置了5块固定标准地。在标准地内进行每木检尺,逐株测定胸径、树高、第一活枝高和冠幅等主要测树因子。每块标准地根据每木检尺结果进行归类,并按径阶由小到大的顺序采用等断面径级标准木法将林木分为5级,计算各径级的平均直径及平均高,以此为标准在标准地外选择5株标准木作为枝解析样木[9]。枝解析的具体做法详见参考文献[10]。
2.2 楠木树冠体积的计算[11]
树冠体积的测量是将树冠按轮枝分成若干层,利用每层的标准枝与树冠的夹角计算每冠层的树冠半径和树冠半径的垂直位置。然后计算每冠层的横断面面积,按照平均断面积求积法计算每相邻两冠层的树冠体积。最上一段树冠体积与最下一段树冠体积的计算可假想为两个正反方向的圆锥体进行计算;对25株标准木按此方法测算其树冠体积,结果见表1。
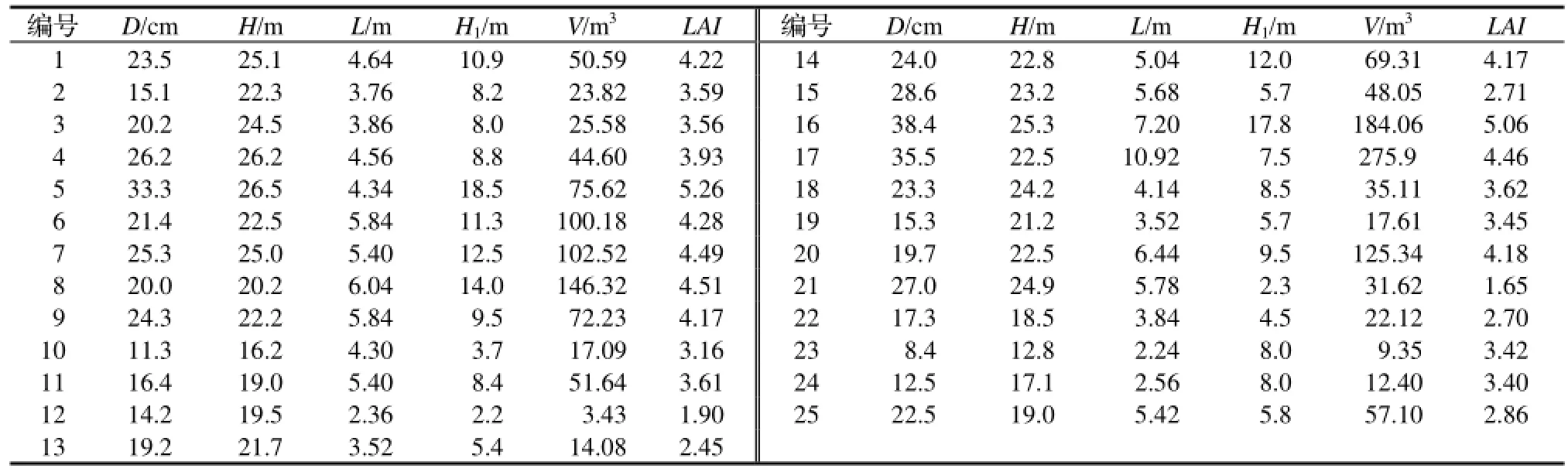
表1 标准木各项因子测算Table 1 Summary of tree variables for branch analysis
2.3 楠木叶面积指数的计算[12]
对所选的25株标准木,将树冠按轮枝分成n层,每层取不同枝条着生位置的树叶100片,置于封口袋中,并进行编号记录,带回实验室称其鲜重,记为a1(g);将称重的每层100个叶样品叠加到一起,然后用打孔器进行叶面积取样,所打出的100个小圆叶片面积相等,记为b1(m2);再次进行称重,记为c1(g);设该层的叶面积为d1(m2),根据重量与叶片面积的比例计算:
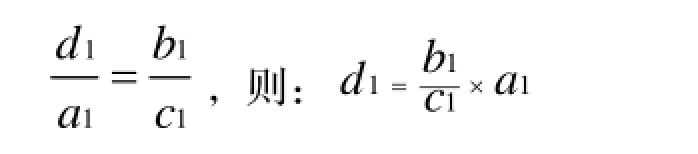
设单株标准木的叶面积为S,叶面积指数为LAI,则:
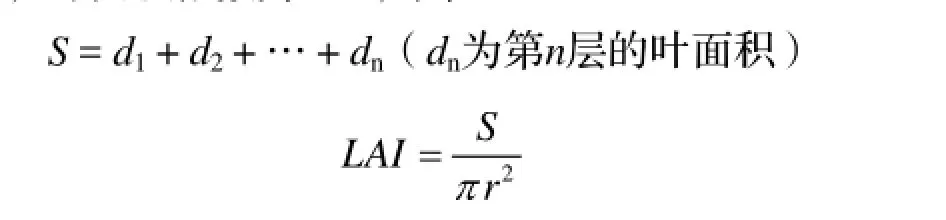
式中,πr2为树冠投影面积(m2),r为树冠半径(m)。
楠木叶面积指数的计算结果见表1。
2.4 建立预估模型
根据表1,用SPSS17进行回归分析,建立预估模型。
3 结果分析
3.1 楠木树冠体积的预估模型
3.1.1 楠木胸径、树高、冠幅、冠高与树冠体积的关系 根据表1的数据,用Excel作图,楠木胸径、树高、冠副、冠高与树冠体积的相关关系见图1至图4。

图1 胸径与树冠体积的相关关系Figure1RelationshipsbetweenthecrownvolumeandDBH

图2 树高与树冠体积的相关关系Figure2Relationshipsbetweenthecrownvolumeandheight
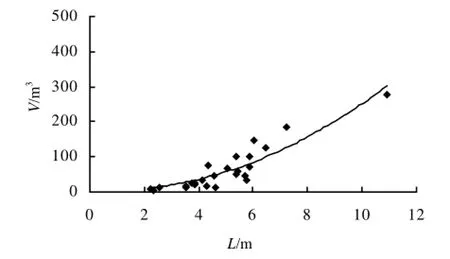
图3 冠幅与树冠体积的相关关系Figure3Relationshipsbetweenthecrownvolumeandcrownsize

图4 冠高与树冠体积的相关关系Figure4Relationshipsbetweenthecrownvolumeandcrownheight
从图1至图4可以看出,树冠体积均随胸径、树高、冠幅、冠高的增大而增大,呈幂函数关系。
3.1.2 建立楠木树冠体积的预估模型 根据表1的数据,对楠木树冠体积的预估模型进行曲线拟合,通过对胸径、树高、冠副、冠高与树冠体积的拟合计算,结果模型的相关系数均较小;对表1中的胸径、树高、冠副、冠高以及树冠体积分别取自然对数后,进行曲线拟合,结果表明树冠体积与冠副、冠高的相关系数最大,其最佳模型为:

式中,R= 0.991,R2= 0.983,sigf = 0.000。
两边取对数即得:

3.2 楠木叶面积指数的预估模型
3.2.1 楠木胸径、树高、冠幅、冠高与叶面积指数的关系 根据表1的数据,用Excel作图,楠木胸径、树高、冠副、冠高与叶面积指数的相关关系见图5至图8。
从图5至图8可以看出,胸径与叶面积指数呈多项式曲线相关关系,树高与叶面积指数呈线性相关关系,冠幅、冠高与叶面积指数均呈对数曲线相关关系。叶面积指数均随胸径、树高、冠幅、冠高的增大而增大。
3.2.2 建立楠木叶面积指数的预估模型 根据表1的数据,对楠木叶面积指数的预估模型进行曲线拟合,通过对胸径、树高、冠副、冠高与叶面积指数的拟合计算,结果表明冠高与叶面积指数的相关系数最大,其最佳模型为三次多项式(CUB)模型:
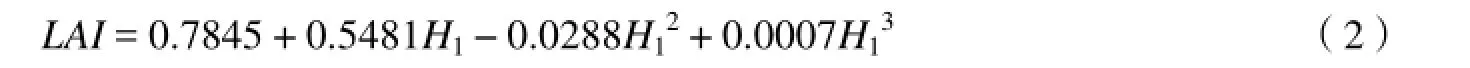
式中,R= 0.937,R2= 0.878,sigf = 0.000。

图5 胸径与叶面积指数的相关关系Figure5RelationshipsbetweentheLAIandDBH
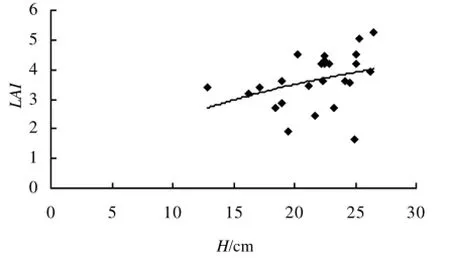
图6 树高与叶面积指数的相关关系Figure4RelationshipsbetweentheLAIandheight
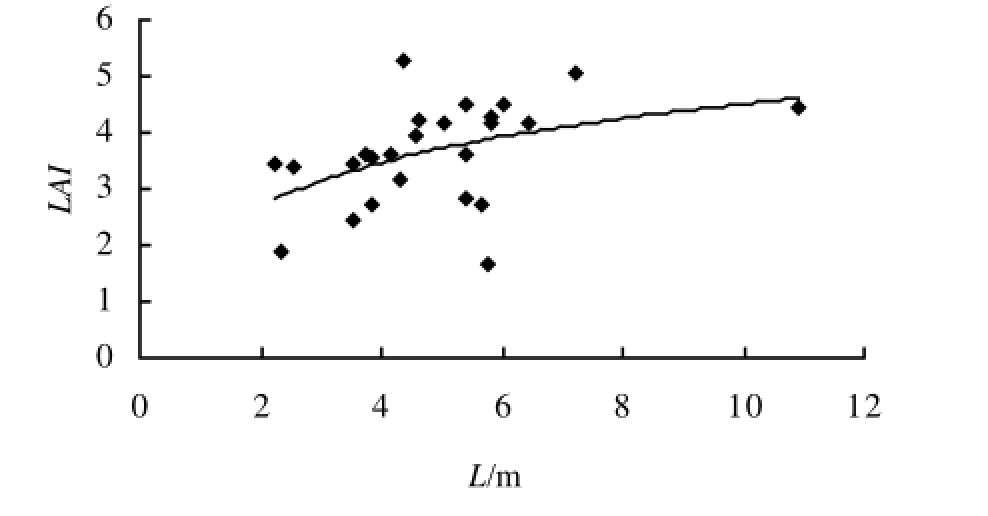
图7 冠幅与叶面积指数的相关关系Figure7RelationshipsbetweentheLAIandcrownsize

图8 冠高与叶面积指数的相关关系Figure8RelationshipsbetweentheLAIandcrownheight
3.4对楠木树冠体积与叶面积指数预估模型的检验
为验证所建模型(1)和模型(2)的有效性,将5块枝解析样地中计算出的各样木V和LAI作为实测值,将模型计算的各样木V和LAI作为理论值,进行了预估误差和精度检验,结果见表2。
4 结论
(1)楠木树冠体积和叶面积指数均随胸径、树高、冠幅和冠高的增大而增大,其中树冠体积与胸径、树高、冠幅和冠高均呈幂函数关系;而叶面积指数与胸径呈多项式曲线相关关系,与树高呈线性相关关系,与冠幅、冠高均呈对数曲线相关关系。
(2)本研究所建立的楠木人工林树冠体积的预估模型为:V= 0.2750L2.253H10.770;叶面积指数的预估模型
为:LAI= 0.7845+0.5481H1-0.0288H12+0.0007H13。
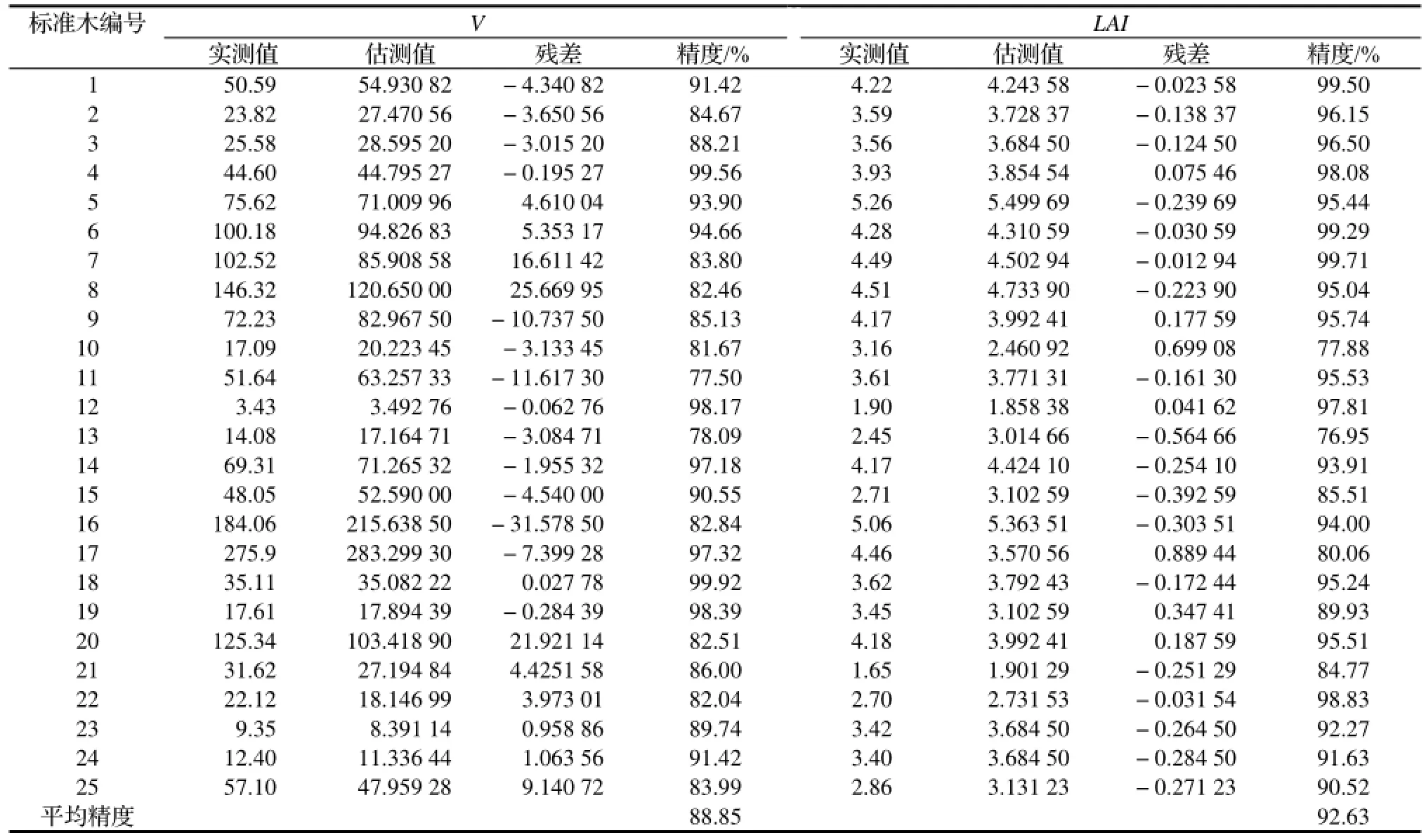
表2 楠木树冠体积和叶面积指数预估模型的检验Table 2 Test re sults of crown volume model andLAImodel forPh. zhennanplantation
(3)文中所建立的树冠体积预估模型(1)和叶面积指数的预估模型(2)的检验结果表明,模型(1)对楠木人工林树冠体积估测的最高精度为99.92%,最低精度为77.50%,平均精度为88.85%;模型(2)对楠木人工林叶面积指数估测的最高精度为99.71%,最低精度为76.95%,平均精度为92.63%。模型(2)的预估效果明显好于模型(1);二个模型的估测精度均大于88%,这说明所建模型预估精度较高,具有良好的适用性。因此,利用这两个模型可以预估楠木人工林的树冠体积和叶面积指数,为进一步研究林分经营模型提供基础。
参考文献:
[1] 惠刚盈,胡艳波. 混交林种间空间隔离程度表达方式的研究[J]. 林业科学研究,2001,14(1):23-27.
[2] 刘素青. 森林生态系统经营与自适应模型研究[D]. 长沙:中国林业科技大学,2006.
[3] 胡艳波,惠刚盈. 优化林分空间结构的森林经营方法探讨[J]. 林业科学研究.2006,19(1):1+8.
[4] 郝云庆,王金锡,王启和,等. 崇州林场不同林分近自然度分析与经营对策研究[J]. 四川林业科技,2005,26(2):20-26.
[5] 张小全,赵茂盛,徐德应. 杉木中龄林树冠叶面积密度空间分布及季节变化[J]. 林业科学研究,1999,12(6):612-619.
[6] 朱春全,雷静品,刘晓东,等. 不同经营方式下杨树人工林叶面积分布与动态研究[J]. 林业科学,2001,37(1):46-51.
[7] 郑万均. 中国树木志[M]. 北京:中国林业出版社,1983,795-797.
[8] 牟林山,李金琢. 都江堰气候特点及其对人体健康和疗养的影响[J]. 中国疗养医学,2003,12(1):1-3.
[9] 廖彩霞,李凤日. 樟子松人工林树冠表面积及体积预估模型的研究[J]. 植物研究,2007,27(4):478-483.
[10] 肖锐,李凤日,刘兆刚. 樟子松人工林分枝结构的分析[J]. 植物研究,2006,26(4):490-496.
[11] 刘兆刚,刘继明,李凤日,等. 樟子松人工林树冠结构的分形分析[J]. 植物研究,2005,25(4):465-470.
[12] 刘立鑫,李凤日. 两种测定天然次生林叶面积指数方法的比较[J]. 森林工程,2009,25(3):44-47.
中图分类号:S718.45
文献标识码:A
文章编号:1001-3776(2010)04-0037-05
收稿日期:2010-03-22;修回日期:2010-05-05
基金项目:四川省教育厅自然科学科研基金项目(2005A021)
作者简介:杜娟(1977-),女,四川南部人,讲师,硕士,从事园林植物应用研究;*通讯作者。
The Predicting Models of Crown Volume and LAI for Phoebe zhennan Plantation
DU Juan,FAN Zhi-Xia,YE Ding-Ying,LU Chang-Tai
(The Dujiangyan Campus of Sichuan Agricultural University, Dujiangyan 611830, China)
Abstract:Based on the branch analysis data of 25 sample trees from 5 permanent plots inPhoebe zhennanplantation, the predicting models of crown volume andLAIwere developed according to SPSS as base model by an analyzing the relationship between crown volume andLAIwith tree variables. The result showed that crown volume and LAI increased with DBH, total height, crown length and height. The predicting models of crown volume wasV= 0.2750L2.253H10.770, the predicting model ofLAIwasLAI= 0.7845+0.5481H1-0.0288H12+0.0007H13. The predicting model of crown volume andLAIdeveloped in this paper were evaluated. The test results indicated that the estimated precisions of the stand variables were all greater than 88% for each model, indicating that the models developed were suitable for estimating the crown volume andLAIforP. zhennanplantation.
Key words:Phoebe zhennanplantation; crown volume;LAI; model

