黄土侧向变形的真三轴试验研究

王瑞瑞，骆亚生，赵春明，岳海英

(西北农林科技大学水资源与建筑工程学院，陕西杨凌712100)

关于土体的变形，人们研究比较多的是沉降，其实侧向变形也是不可小视的[1]，对土体强度和变形的定量、定性分析都离不开对土体应力—应变关系的研究。广义胡克定理中的泊松比μ是反映侧向变形的重要参数，其实际意义是切线泊松比[2]。在多数有限元计算中，不考虑泊松比小于0和大于0.5的情况[3]，当泊松比大于0.5时，通常取泊松比等于0.49。实际工程中的应力状态往往要比轴对称复杂得多，如土体开挖和蓄水、枯水期中坝体中的应力状态的变化，较难满足σ2等于 σ3这一条件[4]。即使σ3比较接近 σ2的情况，其应力—应变关系和侧向变形结果是否也会比较相似呢?对于其它土类，已有学者进行了一些特殊应力路径的研究[5-7]。但对于黄土的研究较少，本试验对多组重塑黄土进行了特定应力路径下的真三轴试验，研究侧向变形规律。

1 材料与方法

1.1 试验仪器

试验仪器为日本谷藤机械工业株式会社生产的TS-526型多功能三试验轴仪，可做圆柱形试样的常规三轴和方柱形试样的3个主应力单独加荷的真三轴试验。方柱形试样的尺寸为88.9 mm×88.9 mm×35.56 mm(图 1)。

试验过程中，可在水平和垂直方向对试样施加各自独立的应力。采用移动边板对试样进行K0固结，其位移用位移传感器测出，水平应力σ3用液压通过橡皮膜加到试样上，而液压作用在侧板上。水平应力σ2用可移动侧板来施加。这两个水平应力的加载都由应力控制。轴向荷载通过量力环及传压板到试样上，并由轴向加载装置控制，采用应变式加载。

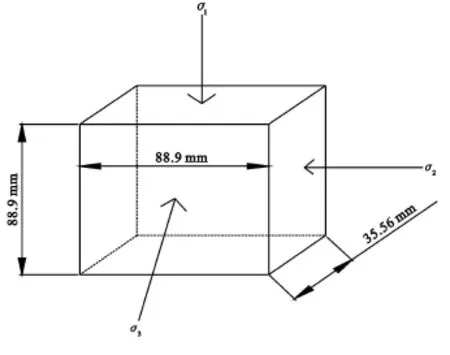
图1 试样尺寸示意图(单位:mm)

1.2 试样制备

试验所用黄土来自陕西省杨凌区，取土深度2～3 m，属于Q3黄土。天然干密度为1.26 g/cm3，孔隙比为1.05，天然含水率为16.1%，其物理性质指标如表1所示。

重塑黄土试样制备时，按要求配置不同含水率的土，静置48 h以上，待水分均匀后，控制含水率之间的差别在0.02%之间，用真三轴压样器分4次缓慢、匀速压制而成。这样既可以精确地制成试验所需干密度(最大干密度1.60 g/cm3)的试样，又可以避免因水膜转移法带来的试样内部含水不均匀带来的试验误差。试样如图2所示。

1.3 试验方法

试验采用不排水固结方式，分别对3个不同的含水率15%，19%，23%进行真三轴试验。首先将σ3增加到 100 kPa等向固结后 ，σ1，σ2增加到 120 kPa，固定 σ2，只增加σ1剪切。这是一种较特殊的应力路径，σ2值较接近σ3的值。增大σ1剪切过程中记录量力环的变形量、轴向位移、两个水平方向的侧向位移，破坏标准取大主应变达到15%。

表1 黄土土样的物理性质指标

图2 土样试验前后对比

2 结果和分析

2.1 应力—应变关系

图3是不同含水率的重塑黄土的排水剪切试验结果(图3 为 q—Δ ε1关系曲线;q—Δ ε2 和 q—Δε3关系曲线略)，其中 q=σ1-σ3为最大主应力与最小主应力的偏差应力，Δε1，Δ ε2，Δε3分别是大主应力 、中主应力和小主应力方向的应变增量。为保证精度，采用多项式拟合，呈现硬化型特点;应变负号表示膨胀，正号表示压缩。

图3 不同含水率重塑黄土的应力—应变(q—Δε1)关系

由图3可知，q—Δ ε1关系曲线的初始切线模量、偏差应力和破坏时的偏应力差随着含水率的减小而增大，应力应变关系曲线由弱硬化转换为强硬化性。在一定的偏差应力下，中、小主应力方向侧向应变随着含水率的增大而增大;在一定的含水率下，中主应力方向刚开始表现为压缩，但表现不是很明显，很快就转为膨胀，总体上表现为膨胀，小主应力方向始终表现为膨胀，且最终膨胀量大于中主应力方向膨胀量，说明了含水率是影响土体强度和变形的一个主要因素。由于试样为重塑非饱和黄土，因此可以忽略矿物的胶结对土体强度影响，随含水率的增加，土体强度的降低实际上可以用非饱和土的强度机理进行解释。随着含水率的增加，破坏了土体颗粒连接处的收缩膜，收缩膜的作用降低，进而使得土体吸力的降低，宏观上就表现为土体强度的降低。

2.2 主应变间的关系

图4—5是含水率为15%和19%条件下的Δε2(Δε3)—Δε1关系曲线和 μ21(μ31)—Δ ε1 关系曲线(w=23%条件下的关系曲线图略)，其中 μ21，μ31是直接对 Δε2—Δε1，Δε3—Δε1关系拟合后的拟合函数求取一次导数的结果。由图中可知，不同含水率的泊松比具有相似的变化规律。中主应力方向在σ1增大的过程中总体表现为膨胀 ，μ21大于 0，且随着 Δ ε1的增大而逐渐减小，说明 Δ ε2变化越来越慢。小主应力方向也随着 σ1的增大而膨胀，μ31大于0，且随着 Δε1的增大逐渐增大，说明Δ ε3的变化越来越快。由图中数值可以看出，μ31渐渐大于0.5。从侧向变形对比来看，小主应力方向最终变形量要比中主应力方向最终变形量大，且随着 σ1的增大 Δε3变化越来越快，到达某一值时变化值大于 Δ ε2 变化。由 Δε2和 Δ ε3 曲线在数值上和变化规律上不同，说明重塑黄土在侧向变形上存在各向异性。

图4 含水率15%条件下侧向应变、侧向变形泊松比关系

图5 含水率19%条件下侧向应变、侧向变形泊松比关系

3 结果分析

室内真三轴试验是对土体三维受荷比较真实的再现，而常规三轴试验只能研究轴对称的应力状态，在反映土体强度和变形的应力—应变关系上也就存在较大差异，尤其是侧向变形的特性。对于本次真三轴试验所研究的重塑黄土，影响侧向变形的因素主要是加载历史或应力路径产生的影响。

施加σ3并使之稳定于100 kPa固结，这一过程并没有扩大试样各向异性的倾向，但当σ1和σ2同时增至120 kPa时，就造成σ2和σ3方向变形倾向的差异 ，也就进一步造成 σ1，σ2和 σ3方向变形的各向异性，在各向不均等的的压力作用下反映出次生各向异性 。因此，当把 σ3=100 kPa，σ1=σ1=120 kPa 应力状态当做相对的初始应力状态，增大σ1受剪时，实际上已经是各向异性条件下的剪切过程。由于σ1＞σ2＞σ3，土颗粒受力不平衡，因 σ3最小，此方向只能表现出膨胀，σ1最大，此方向一直表现为压缩。而σ2介于 σ1和σ3之间，Δε2的正负号要取决于偏差应力 q的大小，初始 q为120～100 kPa，等于20 kPa，比较小，故中主应力方向刚开始剪切时表现出很小的压缩，随着偏差应力的增大很快就转为膨胀。在σ1增大的过程中，最终导致土粒开始反方向的挤压、滚动，宏观上表现为土颗粒沿σ2和 σ3膨胀。

因此，增加σ1试样受剪过程中，试样内部土粒的移动，实际上是3个主应力方向的“合运动”，是大、中、小主应力耦合作用的结果。

4 结论

(1)应力—应变关系曲线的偏差应力和初始切线模量随着含水率的增大而减小 ，Δ ε2和 Δ ε3变化随着含水率的增大而增大，相同含水率下的Δ ε3变化比Δε2变化大。

(2)最小主应力方向始终是膨胀的，由于中主应力的影响，反映在切线泊松比上，有大于0.5的情况。

(3)在上述应力路径下，中主应力方向可以表现出一定压缩，然后转为膨胀。

(4)对于黄土这种弹塑性材料，弹性模量和泊松比不再具有物性参数的意义，而是一种随应力状态及加荷方式变化的状态参量。

(5)对于黄土这种弹塑性材料，在进行有限元计算时，在某些应力路径下，仅仅调整泊松比接近0.5，有可能出现较大的误差，甚至导致严重错误。

反映侧向变形的泊松比的计算，依赖于对试验数据的拟合，尽管拟合所采用的函数表达式不是惟一的，但拟合后的函数几何形态及其一阶导数的值应是一致的，拟合结果可依据均方差之和、置信度等来优化选择。如何寻求和采用最佳的数值拟合方法，也是研究侧向变形的关键问题之一。本试验选用了多项式拟合的方法，对其它的拟合方法未做深入探讨。

现在对于黄土的研究很多并不考虑初始应力状态、加荷方式以及中主应力对土体侧向变形的影响，这与工程实际有较大的差异。而真三轴试验也由于试验仪器、试验方法等多方面的条件限制，要反映所有的工程实际也存在一定的困难，因此真三轴试验的深度和广度也有待进一步的深入研究。

[1] 殷宗泽.土体的侧向变形[C]//第三届全国青年岩土力学与工程会议论文集.南京:中国建筑工业出版社，1998.

[2] 钱家欢，殷宗泽.土工原理与计算[M].江苏:中国水利水电出版社，1995:57-60.

[3] 殷宗泽，朱俊高，卢海华.土的弹塑性柔度矩阵与真三轴试验研究[C]//第七届土力学及基础工程学术会议论文集.北京:中国建筑工业出版社，1994，139-144.

[4] 殷宗泽.高土石坝的应力与变形[J].岩土工程学报，2009，31(1):1-14.

[5] 徐志伟.砂土侧向变形的真三轴试验研究[J].岩土工程学报，2000，22(3):371-374

[6] 徐志伟，陈瑜瑶.淤泥土应力—应变矢量增量的真三轴试验研究[J].岩土力学，2000，21(4):343-349.

[7] 朱俊高，卢海华，殷宗泽.土体侧向变形性状的真三轴试验研究[J].河海大学学报，1995，23(6):29-33.