基于栅格的分布式SCS产流模型研究
罗鹏,宋星原
(武汉大学水资源与水电工程国家重点实验室,湖北武汉430072)
流域水文模型是研究流域水文特性最重要的手段。具有一定物理基础的分布式流域水文模型是当前水文模型的发展方向。其原因在于分布式水文模型具有分析流域特征变化,特别是人类活动所造成的流域特征变化对流域产汇流的影响的潜在能力——虽然这种能力并未在目前成为真正的事实,但是分布式水文模型的不断发展已经不断的展示这种能力,其模拟的精度和合理性也在不断的提高。
对任意一个水文模型来说,其模型必然存在两部分:一是产流部分,另一个是汇流部分。产流模拟是降雨径流模拟的关键,其模拟精度直接影响到最终的出口断面的场次洪水事件的总径流量,并且也影响出口断面的洪水过程形状。因此,建立一个好的分布式产流模型对于研究全流域水文特性是十分重要的。
SCS产流模型是美国农业部水土保持局研制的一个小流域产流估算模型[1]。该模型的两个主要的特点是:(1)模型结构简单,模型中只有一个参数,即CN(曲线数);(2)模型能够反映不同土壤类型、土地利用方式、前期土壤含水量对流域产流的影响。正是由于以上两个突出的特点,使得SCS产流模型得到了广泛的应用,尤其是在无资料地区,更是充分体现了模型的适应性和实用性。但是,传统的SCS模型是一个集总式的产流模型,其无法获得空间分布式的流域产流情况[2]。同时,也由于其将流域概化为一个均匀单一的下垫面,其应用在大流域上的模拟精度也受到限制。本研究正是基于SCS模型的特点及水文模型的发展趋势,将SCS模型与分布式水文模型原理相结合,研究基于格栅的SCS分布式产流模型,形成一个结构简单,参数意义明晰的单元栅格产流模型,提高模型的模拟精度,并使得其能够获取分布式的流域产流结果。并将所构建的基于栅格的SCS模型应用到实际流域中,分析了模型的结构及模拟精度。
1 SCS产流模型基本原理
1.1 模型基本原理
SCS模型的建立是基于一个基本的假设,即流域集水区的实际入渗量与实际径流量之比等于集水区该场降雨前的最大可能入渗量与最大可能径流量之比[3],用公式表达为:

式中:F——实际入渗量;Q——实际产流量;S——最大可能下渗量;Qm——最大可能产流量。经过推导,可以得到计算产流量的公式(2):

式中:P——降雨量;Q——实际产流量;S——模型参数[4]。
SCS产流模型通过一个无因次参数CN(curve number)来推求公式中的未知参数S。CN是一个经验性的综合反应降雨前流域下垫面特征的参数。S的计算公式为:
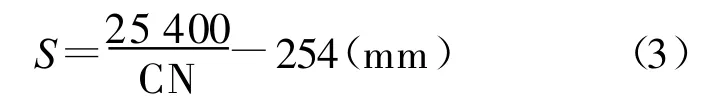
公式(1—3)即为SCS产流的计算公式。
1.2 CN的取值
从上文模型介绍可以看出,SCS产流模型只有一个参数,即CN。并且CN值越大,就意味着更高的径流量和低的渗透量,也就是流域产流能力越强;相反,CN值越小,则意味着更低的径流量和高的渗透量,也就是产流能力越弱。因此,流域取多大的CN值,就决定了流域有多大的产流能力[5]。理论上来说,CN的取值范围为0~100,但是在实际的流域下垫面条件下,CN通常在30~100之间变化。对于某一个特定流域来说,CN取值的具体步骤为:
(1)确定流域的土壤类型。SCS模型中有4类土壤类型,分别为A,B,C,D。其各类的最小下渗率值依次减小。分类的主要的目的是区分和表征不同的土壤渗透率对产流的影响[6]。
(2)确定流域的土地利用类型。土地利用类型是指流域下垫面自然的或人为的植被覆盖种类。各种不同的划分条件及划分目的会产生不同的土地利用类型。土地利用类型的划分综合区分了下垫面植物截流,蒸腾作用,地表透水性能等一系列的产流因素。
(3)确定前期土壤含水量。对于同一个流域,不同的前期土壤含水量状态,会造成最终产流量的很大不同。在SCS模型中,利用降雨前5 d的总降雨量的AMC三级划分指标来定义土壤前期湿度状况[7]。
一般来说,只需要确定AMCⅡ条件下不同土壤类型及土地利用类型的CN取值表,然后利用下列公式[8],可以推求AMCⅠ,AMCⅢ条件下相应的CN值:

(4)通常情况下,流域的土壤类型,土地利用类型并不单一,常常是各土壤类型及土地利用类型各占一定的比例。此时,分别确定不同土壤及土地利用类型的耦合分类Ci的CN值,并计算各分类占总流域面积的百分比Pi,最后流域总的CN计算公式为:

式中:n——不同土壤及土地利用类型的耦合分类Ci的总个数。
利用确定的CN值,即可利用公式(2)来计算次降雨的产流量。
2 基于栅格的SCS产流模型方法
2.1 SCS产流模型分析
从以上对于原始SCS产流模型的原理介绍可以看出,虽然SCS产流模型的总体结构简单,且只有一个参数,但是模型的结构决定了,其将模型模拟的精度全部转移到了CN这一个参数的上。也就是说,对于单个的流域,模型只能选择一个CN值来代表全流域,这就造成了CN值的选取的困难。
同时,流域产流的不均匀性主要体现在两个方面,一是下垫面特性的不均匀性,包括土壤特性,土地利用情况,及前期土壤含水量等;另一个是降雨的空间分布不均匀性。前者是内因,后者是外因。两者的共同作用,使得流域的产流在空间上变得极不均匀。因此,如何综合考虑这些因素是获得较高精度的产流结果的关键。但是,原始的SCS模型无法精细的考虑这些因素,只能用流域平均的方法来粗略考虑这些因素对产流的影响。对于流域面积较小的小流域来说,用流域平均的方法可以满足精度的要求,但是在较大的流域上,这种方法将会造成很大的误差。
2.2 基于栅格的SCS产流模型方法
综上对原始 SCS模型的分析,本研究改进了SCS产流模型结构,将其与地理信息系统结合起来,将流域划分成许多个大小相同的栅格。假定栅格内的所有产流特性是相同的,可以用一个CN值来表示,而不同的栅格则可能不同。对于降雨,则同样以所划分的栅格为主体,利用降雨空间插值方法,如最短距离法,距离平方反比法等等,将流域内所布设的雨量站的降雨数据插值到每个栅格上。这样,SCS模型的产流计算则转化到计算每一个子栅格上来,从而细化了流域的特性,在一定的程度上考虑了下垫面和降雨量的空间不均匀性。
基于以上的模型构建可以看出,改进后基于栅格的SCS模型的构建的重点将是获得每一个单元栅格上的CN值。根据SCS模型对于CN的定义,假定在相同的土壤类型、土地利用状况及前期土壤含水量条件下,CN的取值是相同的,这样就可以按照每个栅格不同的地理属性状态来给定该栅格的CN值。可以分析得出,对于不同的流域来说,只需要一张处于AMCⅡ分组条件下的,不同土壤类型与土地利用状况下所对应的CN取值表即可。其它土壤干湿状况下的CN取值,可通过公式(4—5)转化得到。
在实际的研究中发现,改进后模型最终的模拟结果受前期土壤含水量AMC分类的影响很大。考虑到不同流域所处的地理位置的不同,其降雨的特点和蒸散发能力都不同,只考虑5 d内的降雨对前期土壤湿度的影响是非常不够的。往往在湿润地区的流域,其土壤在雨季大部分时间都处在中等湿度状况下,其土壤湿润并不由5 d内是否有降雨所决定。而且,在某些情况下,流域在5 d内并没有降雨,但是在5 d之前却下了大雨,这样土壤仍然会很湿润,如果只考虑5 d的降雨影响,会造成很大的误差。
基于以上的讨论,本研究改进了对前期土壤湿度划分标准。改进后的判断标准的判断步骤为:(1)首先按照原有的SCS模型判断AMC土壤湿度分类,当某栅格的土壤被划分为AMCⅡ,AMCⅢ,则忽略以下步骤;若为AMCⅠ时,则进行下一步判断;(2)当本场次降雨前的5 d内的降雨量小于5 mm,则认为流域基本为晴天,蒸散发能力很强。5 d之前的降雨可以被蒸发完全,既不考虑5 d前的降雨影响,并确认栅格的土壤湿度分类为AMCⅠ,并忽略以下步骤;否则,认为流域基本为阴雨天气,蒸散发能力弱,5 d前的降雨会对土壤湿度产生影响,应考虑5 d前的降雨影响,并进行下一步判断;(3)若本场次降雨前的第6,7,8,9,10 d该栅格上的总降雨量大于原有的SCS模型判断AMC土壤湿度分类标准的AMCⅢ所规定的降雨量时,则修正其土壤划分标准为AMCⅡ。
实际计算结果表明,由以上的步骤所获取的网格湿度分类所计算得到的产流结果比原始的只考虑5 d内降雨的所得到的各网格湿度分类要准确。模型的模拟精度得到了很大的提高,减小了对网格AMC湿度分组的不准确性。
3 实例应用
3.1 流域概况
欧阳海水库流域位于湖南省东南部地区,为湘江一级支流舂陵水中游。水库流域面积为5 409 km2,该流域有15个雨量站及两个水文站和一个流域控制站,且雨量站在流域内分布均匀。流域内以丘陵为主,丘陵面积约占总面积70%。表层土壤中主要有红壤土,红黄壤土,水稻土,以及山地红黄壤复区4种类型。
3.2 数据资料
根据欧阳海流域1 km网格精度的DEM进行填洼,再提取出流域水文因子及流域河网。欧阳海流域植被覆盖类型主要有:草地、林地草原、农田、林地、常绿针叶林,以及少量的水域、常绿阔叶林、落叶阔叶林。表1给出了土地利用各分类所占流域面积的百分比。欧阳海流域土壤类型是参考了全国土壤普查得到的土壤分布资料[9]及实地考察获取的土壤资料分析得到的。表2给出了流域各土壤类型所对应的SCS土壤分组。

表1 各土地利用类型所占流域面积的比例
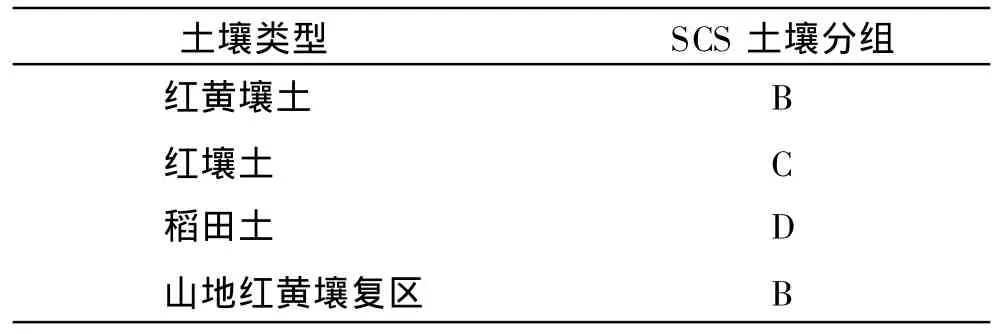
表2 不同土壤类型的SCS土壤分组
欧阳海流域上的水文资料有1990—2009年共44场洪水事件的入库流量资料,以及15个雨量站1990—2009年小时时序的降雨量资料。首先按照基于格栅的SCS模型的要求将数据整理成模型所需要的格式,其中降雨量的栅格空间差值方法采用最短距离法,然后将其应用于模型计算。
3.3 栅格CN值的确定
根据以上的原始资料的处理分析、考察美国SCS模型CN取值表[10]和国内关于CN取值的研究经验成果[1-7],得到该流域在AMCⅡ条件下不同土地利用类型和不同土壤类型下的耦合CN取值表(表3)。其它前期土壤湿度分类条件下的栅格CN由公式(4—5)转化得到。

表3 研究流域在AMCⅡ条件下的CN值
4 结果分析
将以上的CN取值应用到流域栅格上,分别计算每场降雨情况下每一个栅格的产流量,并对流域内所有栅格的产流进行累加。然后将其与实测的流域出口处洪水过程总量以及原始SCS模型的计算结果进行比较。
图1给出了两个模型的计算结果与实测产流量的对比图。图2给出了每场降雨的各类AMC土壤分类相应的栅格个数。图3给出了两个模型的产流具体计算结果的相对误差对比关系图。从图1可以看出,利用栅格SCS模型计算的产流量的点要比原始SCS模型的计算结果更靠近直线y=x,说明其计算结果的绝对误差要小于原始SCS模型。从图3中可以看出,改进后的SCS产流模型有26场降雨的误差达到了15%以内,有38场达到了30%以内,最大的误差也只有50.5%。而原始的SCS模型只有12场降雨的精度达到了15%以内,且其误差区间很大,最大的误差为-83.4%。从总体来看,改进后的SCS产流有33场的模拟精度均优于原始的SCS模型。
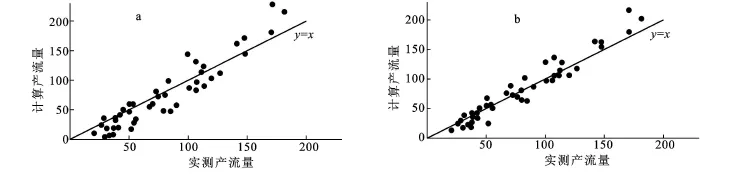
图1 模型计算结果与实测产流量对比(mm)注:a为原始SCS模型计算结果,b为栅格SCS模型计算结果。
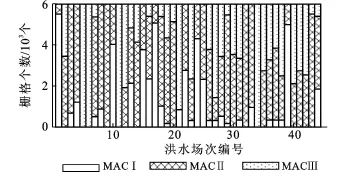
图2 各洪水场次的前期AMC土壤分类栅格个数
对于洪水编号为“19940804”的洪水(图3中横坐标编号为13),可以看出,由于流域前期降雨空间分布不均匀,造成了不同位置的栅格的土壤湿度AMC分类不同。
在这样的情况下,以栅格方式计算产流量时,充分考虑到流域前期降雨的空间分布,并将流域不同区域的栅格的AMC分组划分好。这样模型的计算精度就从原来的-36.0%提高到-4.4%。

图3 基于格栅的SCS模型与原始SCS模型计算结果相对误差对比
值得说明的是,在前期土壤湿度分类为AMCⅡ条件下,原始SCS模型中的全流域平均 CN值取84.02,这个值是根据栅格SCS模型的AMCⅡ条件下的所有栅格CN值取平均而得到的。因此,这也说明了原始SCS模型的结果也部分利用了基于栅格的SCS模型的成果。
5 结论
通过将GIS技术与现有的SCS模型相结合,构建了一个基于栅格系统的SCS模型,该模型同样保持了原有SCS模型结构简单,参数少的特点,并在改进后增加了其在大流域下垫面空间不均匀以及降雨空间分布不均匀情况下的模拟能力,从而扩大了模型的适应性。
分布式水文模型是当前水文模型的方向,但是资料的获取难度使得模型的应用变得非常的困难。因此,对于这样的一种对资料输入要求并不高的栅格SCS模型,可以在一定程度上改善分布式水文模型对资料情况的适应能力,从而更好地推动流域水文模拟的研究以及流域水资源管理的发展。
[1] 许彦,潘文斌.基于ArcView的SCS模型在流域径流计算中的应用[J].水土保持研究,2006,13(4):176-179.
[2] 刘贤赵,康绍忠,刘德林,等.基于地理信息的SCS模型及其在黄土高原小流域降雨—径流关系中的应用[J].农业工程学报,2005,21(5):93-97.
[3] 郑畅,倪九派,魏朝富.基于DEM和SCS模型的四川盆地丘陵区局地径流研究[J].水土保持学报,2008,22(5):73-77.
[4] 罗利芳,张科利,符素华.径流曲线数法在黄土高原地表径流量计算中的应用[J].水土保持通报,2002,22(3):58-61.
[5] 张美华,王晓燕,秦福来.SCS模型在密云石匣试验小区降雨径流量估算中的应用[J].首都师范大学学报:自然科学版,2004(25):155-158.
[6] 张秀英,孟飞,丁宁.SCS模型在干旱半干旱区小流域径流估算中的应用[J].水土保持研究,2003,10(4):172-174.
[7] 詹道江,叶守则.工程水文学[M].3版.北京:中国水利水电出版社,2000:161-166.
[8] Budhendra B,Jon H ,Bernie E,et al.Assessing watershed-scale,long-term hydrologic impacts of land-use change using a GIS-NPS mode[J].Environmental Management,2000,26(6):643-658.
[9] 湖南师范学院地理系.湖南农业地理[M].长沙:湖南科学技术出版社,1981:26-32.
[10] U.S.Department of Agriculture,Soil Conservation Service.Hydrology[M].SCS National Engineering Handbook,Section 4.U.S.Gov.Print Office:Washington D.C.,1972.

