基于多维建模的滑坡监测数据挖掘

朱传华，胡光道

(中国地质大学资源学院，湖北武汉430074)

安全监测是研究和防治滑坡的重要手段之一，而位移监测又是滑坡监测中一种最常用的监测手段[1-2]。对滑坡监测历史数据分析，有利于发现滑坡发生的模式，从而进一步预报滑坡发生的时间。知识发现和数据挖掘技术能从大量的数据中抽取出具有一定规律的知识，为决策分析带来了新的途径，能更好地解决日益复杂多变的决策环境问题，进一步提高决策的准确性和可靠性，为科学决策提供了基础。数据挖掘技术已经广泛应用于银行、电信等商业领域，近几年，云模型[3]、关联规则[4]、支持向量机[5]和BP神经网络模型[6]等数据挖掘技术在滑坡监测数据分析方面的探索研究也逐步展开。本研究运用了Microsoft时序算法对滑坡监测时间序列数据进行分析。

1 时间序列分析及其在滑坡监测中的应用

滑坡位移及其影响因素的监测数据是两类相对独立的随机样本，目前常用时间序列分析模型解析其响应关系[2，6-7]。时间序列通常是按时间顺序产生和排列的一系列被观测数据，其观测值按固定的时间间隔采样。所得数据最为重要和有用的特性就是观测值之间的依赖关系或相关性。利用这种相关性，研究人员以分析过去的历史资料为依据，能预测将来的变化[8]。一般时间序列模型可以由两个基本概念描述:趋势和周期性[9]。滑坡监测时间序列数据也具有这样的特点。郝小员等[7]根据对边坡变形发展过程的位移数据分析，认为滑坡位移观测数据时间序列包括趋势项、周期项和随机项。其中趋势项是由边坡土体的蠕变特性所决定，即滑坡变形破坏严格受内在发展规律的控制。周期项可以理解为温度、降雨等因素影响的结果，反映了滑坡发展过程中位移的周期变换波动。两者叠加就是边坡变形位移的发展趋势的最主要因素，是决定边坡稳定的主导。而随机项可以认为是因突发性因素影响而产生的，如突发性暴雨、地震、人工活动等，反映了边坡变形的一些随机变化。杜娟等[6]认为滑坡位移的产生及变化是坡体自身地质条件和外部诱发条件共同作用的结果，因而其位移总量可以按照各影响因素作用形式的不同分解为不同的响应成分，包含4种成分:趋势项、周期项、脉动项和不确定的随机变量。三峡库水位作为脉动项因素，因其体现较好的周期性特征，所以可作为周期性因子考虑。综上所述，滑坡位移观测数据时间序列包括趋势项、周期项和随机项。在进行滑坡监测时间序列数据分析时，应掌握其特点并理顺其数据概念层次(图 1)。

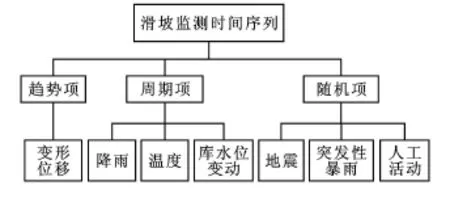
图1 滑坡监测时间序列概念层次

目前常用的时间序列模型有差分自回归滑动平均(ARIMA)、多变量时间序列(CAR)、自回归树(ART)、指数平滑和向量自回归(VAR)等[2，9]。在模式发现的过程中，常用算法需要分析人员合理处理缺失值和调节一些具体设置，如指定周期指标或允许算法自动地发现周期、周期总数或总的时间范围和最小支持阈值等。这样使得分析人员的精力浪费在复杂的求解方法，而非重点解决研究的问题领域。另外，常用的时间序列模型和一些数据挖掘算法使用的输入数据是平面文件[2，4-6]。平面文件的不足之处在于它由大量的列组成，使用的属性不包含它们自身结构的重要信息，分析人员很难理解其中部分列的含义、值的类型和它们之间的关系。整个分析过程依赖于分析人员的专业知识，具有主观性[9]。

2 数据仓库多维建模

本研究引用了一种全新框架，在数据仓库多维模型的基础上进行时间序列的分析[9]。在多维模型中(图2)[10]，数据被组织成多维数据集(立方)和维。度量所在表称为事实表，事实是分析的焦点，是度量的聚积，度量通常是数值数据。每个事实有几个相关的维，维通过描述性属性提供分析的上下文。这些维通过级别被组织成聚集层次，使事实度量能在不同的细节级别上分析。建模过程能帮助分析人员理解数据。模型以分析的事实或维来呈现数据，这种方式表达了研究的问题领域而非某一具体的求解方法。另外，数据仓库中的数据都是根据具体需求集成的，数据在进入仓库之前必须通过数据预处理或ET L过程，数据质量能得到保证。

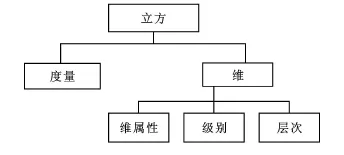
图2 多维模型逻辑图

3 实例应用——以白水河滑坡监测数据为例

3.1 白水河滑坡概况

三峡库区秭归县白水河滑坡位于长江南岸，距三峡大坝坝址56 km，属沙镇溪镇白水河村。滑坡体处于长江宽河谷地段、为单斜地层顺向坡地形，南高北低，呈阶梯状向长江展布。其后缘高程为410 m，以岩土分界处为界，前缘抵长江135 m水位，东西两侧以基岩山脊为界，总体坡度约30°。其南北向长度600 m，东西向宽度700 m，滑体平均厚度约30 m，体积1.26×107m3。白水河滑坡为老滑坡，历史上频繁发生顺层滑坡。滑坡地层为砂岩夹泥岩，属易滑地层，坡体为顺层斜坡，在构造节理切割、长江下切卸荷、后缘崩塌加载和降雨等外力作用下，易产生顺层滑移变形破坏，属堆积体顺层滑坡。白水河滑坡专业监测已于2003年6月开始实施，根据该滑坡的地形地貌、地质条件与监测环境，监测方法有GPS监测、深部位移钻孔测斜监测、地下水位监测和人工巡查等。监测结果初步表明，受三峡水库蓄水及库水位涨落、雨水等作用影响，白水河滑坡整体稳定性变差，地表变形迹象较为明显，位移变化量较大，呈现牵引式滑坡变形特征[6，11]。

3.2 滑坡位移监测多维建模

滑坡是一个集合概念，不同地质环境背景下孕育发生的不同成因机制的滑坡，在多维建模时要合理划分不同的滑坡类别[12]。根据不同的滑坡分类，相应的监测内容和监测仪器也不尽相同[13]。在分析滑坡监测时间序列的特点，并考虑滑坡孕育的复杂性和滑坡监测系统的有效性的基础上，可确定滑坡位移监测事实，及其相关的时间、地点、滑坡类型和监测类型等维，以及累计位移、温度、库水位变动和降雨量等度量，在建模工具Power Designer中建立多维模型。如图3所示，监测类型维有监测类型ID、监测仪器和监测内容，和相应的监测类型层次(图4a)[14]，滑坡监测系统的具体内容可参见[13]。时间维有时间ID、日期、月份、季度和年份等属性和相应的时间层次(图4b)。地点维有地点ID、监测点名、滑坡体名、村名、镇名、县名等属性和相应的地点层次(图 4c)。滑坡类型维有滑坡类型ID、类、型、式、期和性等属性和相应的滑坡类型层次(图4d)。滑坡分类的具体内容可参见[13]和[15]。滑坡位移产生的各影响因素如累计位移、温度、库水位变动和降雨量等作为度量。

图3 滑坡位移监测多维模型注:Default h为默认层次;阿拉数字为层次的级别。

3.3 在SQL Server 2005中的实现

在Power Designer中设计的多维模型经映射等操作后，可在关系数据库中生成多维数据集。在关系数据库中实现多维数据集一般有两种基本结构:星型模式和雪花模式。图5所示是在SQL Server 2005 Analysis Services(SSAS)中生成的星型模式多维数据集，滑坡位移监测事实被映射到中心表，表中包含度量和与相关维连接的外键(时间ID、地点ID、监测类型ID和滑坡类型ID)。星型模式提供了简洁而有组织的仓库结构，便于OLAP操作。

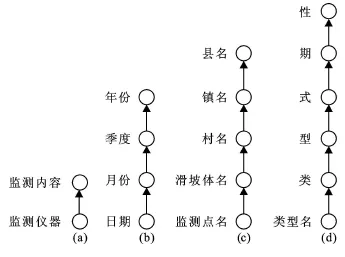
图4 维属性的层次注:a监测类型维;b时间维;c地点维;d滑坡类型维。

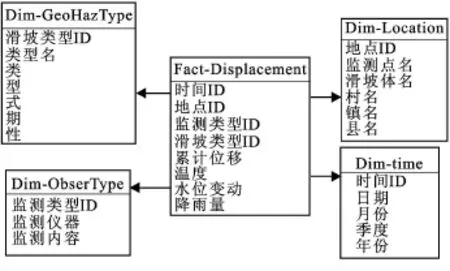
图5 星型模式的滑坡位移监测多维数据模型

在建立多维数据集的基础上，针对滑坡监测时间序列选择合适的数据挖掘技术—Microsoft时序算法。Microsoft时序算法是 SSAS提供的回归算法，用于创建数据挖掘模型以便对预测方案中的连续列进行预测。Microsoft时序算法包括两个独立的算法，其中ARTXP算法是在SQL Server 2005中引入的，针对预测序列中的下一个可能值进行了优化。本研究选取白水河滑坡体ZG93监测点2004年1月至2006年12月期间36个月的水平累计位移数据作为模型训练数据，经Microsoft时序算法挖掘模型处理后，得到回归公式:

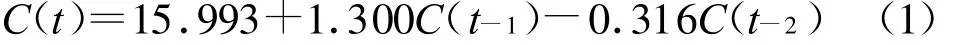
式中:C(t)——某一时刻的位移量值。公式(1)明显反映了位移量和前一个月的相关性(相关系数为1.300)，和周期性的相关性系数为0.316。

预测结果模型由两部分组成(图略):图形左侧的历史信息和图形右侧的预测信息。历史数据表示算法用来创建模型的信息，而预测数据表示模型所做的预测。由图可知，ARTXP算法预测了下一个时间段的数据值，即第37个月的预测数据为626.74，与实测数据632.5相差为1%。结果表明预测效果较好。

4 结论

时间序列分析具有预测复杂系统发展趋势的能力，一直是滑坡位移动态预报研究的热点，然而目前的预测模型多基于平面文件进行分析。本研究引入在数据仓库多维模型的基础上进行时间序列分析的框架——数据被组织成事实和维，滑坡位移产生的各种可能因素被结构化和层次化的展现出来，可帮助分析人员更深入全面地理解滑坡位移事实。使用Microsoft时序算法—ARTXP算法对白水河滑坡位移数据进行挖掘，得到的预测数据与实测数据误差较小，结果表明该算法可以用于滑坡监测数据的短期预测。不足之处在于温度、降雨量和库水位变动等数据尚未收集完整，仅对滑坡位移数据进行了挖掘，没有对位移和库水位、位移和降雨量进行交叉预测，挖掘模型应用的可靠性有待进一步验证。另外，SQL Server 2008 Microsoft时序算法中添加了 ARIMA算法，用于提高长期预测的准确性，可考虑在下一步工作中引入该算法进行滑坡监测的长期预测研究。

[1] 殷坤龙.滑坡灾害预测预报分类[J].中国地质灾害与防治学报，2003，14(4):12-18.

[2] 李强，李端有.滑坡位移监测动态预报时间序列分析技术研究[J].长江科学院院报，2005，22(6):16-19.

[3] 王树良，王新洲，曾旭平，等.滑坡监测数据挖掘视角[J].武汉大学学报:信息科学版，2004，29(7):608-610.

[4] 马水山，王志旺，张漫.基于关联规则挖掘的滑坡监测资料分析[J].长江科学院院报，2004，21(5):48-51.

[5] 董辉，傅鹤林，冷伍明.滑坡变形的支持向量机非线性组合预测[J].铁道学报，2007，29(1):132-136.

[6] 杜娟，殷坤龙，柴波.基于诱发因素响应分析的滑坡位移预测模型研究[J].岩土力学与工程学报，2009，28(9):1783-1789.

[7] 郝小员，郝小红，熊红梅，等.滑坡时间预报的非平衡时间序列方法研究[J].工程地质学报，1999，7(3):279-283.

[8] 吴今培.实用时序分析[M].长沙:湖南科学技术出版社，1989:1-2.

[9] Jose Z ，Jesus P，Juan T.A UM L profile for the conceptual modeling of data-mining with time-series in data warehouses[J].Information and Software Technology，2009，51:977-992.

[10] Oracle USA，Inc.Oracle OLAP Application Developer's Guide 10 g Release 2(10.2.0.3)[M].Redwood:Oracle Press，2006:29-32.

[11] 王尚庆，徐进军，罗勉.三峡库区白水河滑坡险情预警方法研究[J].武汉大学学报:信息科学版，2009，34(10):1218-1221.

[12] 黄润秋，向喜琼，巨能攀.我国区域地质灾害评价的现状及问题[J].地质通报，2004，23(11):1078-1082.

[13] 张振华，罗先启，吴剑，等.三峡库区滑坡监测模型建模研究[J].人民长江，2006，37(4):93-94.

[14] Jiawei H ，Micheline K.数据挖掘:概念与技术[M].北京:机械工业出版社，2006:110-123.

[15] 刘广润，晏鄂川，练操.论滑坡分类[J].工程地质学报，2002，10(10):339-342.