反应位移法在盾构隧道横向抗震分析中的应用

晏启祥，马婷婷，吴 林，耿 萍

(西南交通大学 地下工程系，成都 610031)

城市轨道交通网中城市地下铁道所占比重很大，而城市地铁区间隧道又以盾构法隧道为主［1］，加之我国地下铁道设计中，由于研究工作开展不够，目前《地铁设计规范 》(GB50157—2003)对地铁盾构隧道的抗震设计方法和抗震措施尚无具体规定。尽管目前国内有少数几篇文献［2-4］已经运用了反应位移法进行抗震设计，但对其原理的介绍还不够深入，而且对盾构隧道横断面的模拟基本上还是采用匀质圆环模型。而事实上盾构隧道接头的存在，将明显改变圆形衬砌的地震响应。有鉴于此，本文在系统介绍日本地铁铁道抗震设计的反应位移法［5］的基础上，针对匀质圆环和接头圆环两种模型开展抗震分析，以期推动盾构隧道抗震设计反应位移法的应用和揭示基于盾构隧道接头效应的动力反应。

1 反应位移法原理

地铁区间盾构隧道属于地下结构的一种。地下结构在地震作用时，由于周围岩土介质的存在，会发生不同于地面结构的动力响应。地面结构具有明显的加速度放大效应，而地下结构与附近地层的加速度相对比较接近［5］。地下结构的加入对地层的动力响应影响较小，且地下结构的地震响应很大程度上依赖于地震作用下地层的振动响应。进一步的研究还发现，地层加速度和地下结构应变时程曲线吻合程度远没有地层相对位移和地下结构应变时程曲线吻合程度高，说明地下结构变形对地层变形具有依赖性和追随性［6］。与周围地层相比，地下结构通常具有单位体积重量较小、振动衰减较快、自身惯性力影响较小等特征。反应位移法正是基于地下结构的这些特点而提出的。

假设地下结构只受到水平剪切波的作用。为计算地震作用下结构的地震反应，需首先计算出结构与地层之间的相互作用力和含结构地层的位移。由于结构与地层之间的相互影响是作用力和反作用力的关系，因此可通过空洞地层脱离体获取地层施加于结构上的作用力和地层施加于结构上的位移。空洞地层上的位移和结构对空洞地层的反作用力如图1所示，其中，{FI}为地层结构之间的相互作用力，{uI}为含结构地层在地震作用下的位移。图1(a)为空洞位移，图1(b)为地层弹簧模拟的地层与结构之间的相互作用。对于复杂地层，图1(a)中所示空洞位移的求解并不容易。通常先按天然地层求出地下结构可能发生最大断面力时周围地层的位移分布，再在分析模型上附加一个相当于空洞壁面作用的周边剪切力来实现。空洞地层位移等效如图2所示，图中剪切力为天然地层之间的相互作用力，而非地层和结构之间的相互作用力。

综上，在水平剪切波作用下，采用反应位移法进行地震反应分析最终归结为求解地下结构在地层弹簧约束下，受天然地层最大强制位移差及其对应时刻地层剪切力共同作用下的地震反应［5］。

图1 空洞地层的分解

图2 空洞地层位移等效

2 反应位移法模型和计算流程

根据反应位移法基本原理，进行地铁区间盾构隧道抗震设计时，可将地震荷载分为两部分:一部分是盾构隧道周边天然地层的剪切力;另一部分是盾构隧道两侧受到的强制位移。由于惯性荷载对地下结构的影响很小，这里不予考虑。地震时地层位移沿地层深度方向变化如图3(a)，相应盾构隧道的计算模型如图3(b)。

图3 反应位移法的抗减震计算模型示意

假设地层为单一均匀地层(若地层基岩面上为成层地层，可采用加权平均的方法简化成单一地层并计算其相应的物理力学参量)，地层的运动微分方程为:

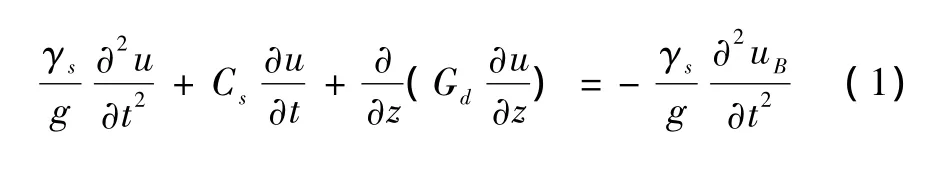
式中:u为地层变位，γs为地层重度，Gd为地层动剪切弹性模量，Cs为地层黏性衰减系数，uB为地层地震动，g为重力加速度。通过求解式(1)并作近似处理可得地层最大位移为

式中:Su为地层基岩面的速度反应谱，Ts为地层的自振周期，z为原点位于地表的向下坐标系变量，H为土层厚。(2)式对z求导并与地层剪切模量相乘得对应天然地层的剪切力:

由于地层剪切力与深度有关，可逐一求出各点的剪切力并进行极坐标转化。也可以取隧道顶部和底部剪切力之和的一半，作为隧道周边剪切力作简化计算。进行直角坐标至极坐标转化后，盾构隧道周边受到的等效径向正应力和剪应力分别为:σ=－τxysin2φ;τ=τxycos2φ，φ为从x轴正向逆时针旋转的角度，而切向正应力不作用在结构上。

沿衬砌周围设置地层弹簧来模拟隧道与地层之间的相互作用［4］。求出地震时隧道断面所在天然地层的位移，剪切波在均质地层中沿水平方向振动时，该地层应力即为地震时的剪切应力。将地震时的地层剪切力沿衬砌的法线和切线方向分解，直接施加在衬砌上;将地震时天然地层的位移沿衬砌的法线和切线方向分解，分别按各自的方向作用于地层弹簧的末端。根据上述结构模型及地震荷载利用大型有限元软件进行结构内力计算，获得地震引起的隧道衬砌断面内力;将常时荷载下的断面内力与地震荷载下的断面内力进行叠加，获得盾构隧道抗震设计所需断面内力。

3 算例

某盾构隧道的外径D=6.3 m，隧道中心至地表面距离12.15 m，隧道上覆土层厚度为9 m，隧道衬砌为平板型钢筋混凝土管片，厚度0.3 m，重度27 kN/m3，弹性模量3.5×104MPa。隧道所处地层为均质黏性土，厚28 m，其下为基岩，经计算其动剪切模量 Gd=93.8 MPa，基岩面速度反应谱 Su=0.156 m/s，土层的自振周期 Ts=0.713 s，地层弹性抗力系数径向 K1=2.3×107N/m3，切向 K2=0.77 ×107N/m3。

3.1 求解地震作用下地层的位移

根据反应位移法的基本原理，将地层位移沿深度分布假设为余弦函数，利用公式(2)计算其地层位移:

3.2 求解地震作用下天然地层的剪切力

将地震剪切力沿深度分布假设为正弦函数，利用公式(3)计算其地震剪切力:

3.3 实施地层剪切力极坐标转化

逐一求出隧道结构各点直角坐标系下分布的剪切力，将其转化为极坐标系下沿衬砌法线和切线方向上的力，直接加载于衬砌上。建立的荷载—结构计算模型如图4所示，图中示出了隧道周边的应力分布规律以及地层弹簧，而强制位移施加在弹簧末端。

图4 荷载—结构计算模型

3.4 在结构上施加强制位移和剪切力并求解结构内力

将以上求出的地震剪切力和地层强制位移作用在结构上，就可计算出地震荷载引起的盾构隧道结构断面内力。将常时荷载下结构断面内力与地震荷载产生的断面内力进行叠加，即可得到抗减震设计所需要的结构断面内力。

这里为说明盾构隧道的地震效应，只讨论地震荷载引起的结构内力，并对简化的匀质圆环盾构隧道与接头圆环盾构隧道两种模型进行对比分析。接头圆环盾构隧道模型用切向、径向和旋转弹簧来模拟管片接头处的铰接作用。衬砌采用3+2+1的分块方式，依次为 3块标准块(3×72°)、2块邻接块(2×54°)和 1块封顶块(1×36°)。利用反应位移法计算获得的匀质圆环盾构隧道模型与接头圆环盾构隧道模型衬砌典型位置结构内力，计算结果列于表1，其中 θ为从x正向进行逆时针旋转的角度，弯矩以内侧受拉为正，轴力以拉为正。

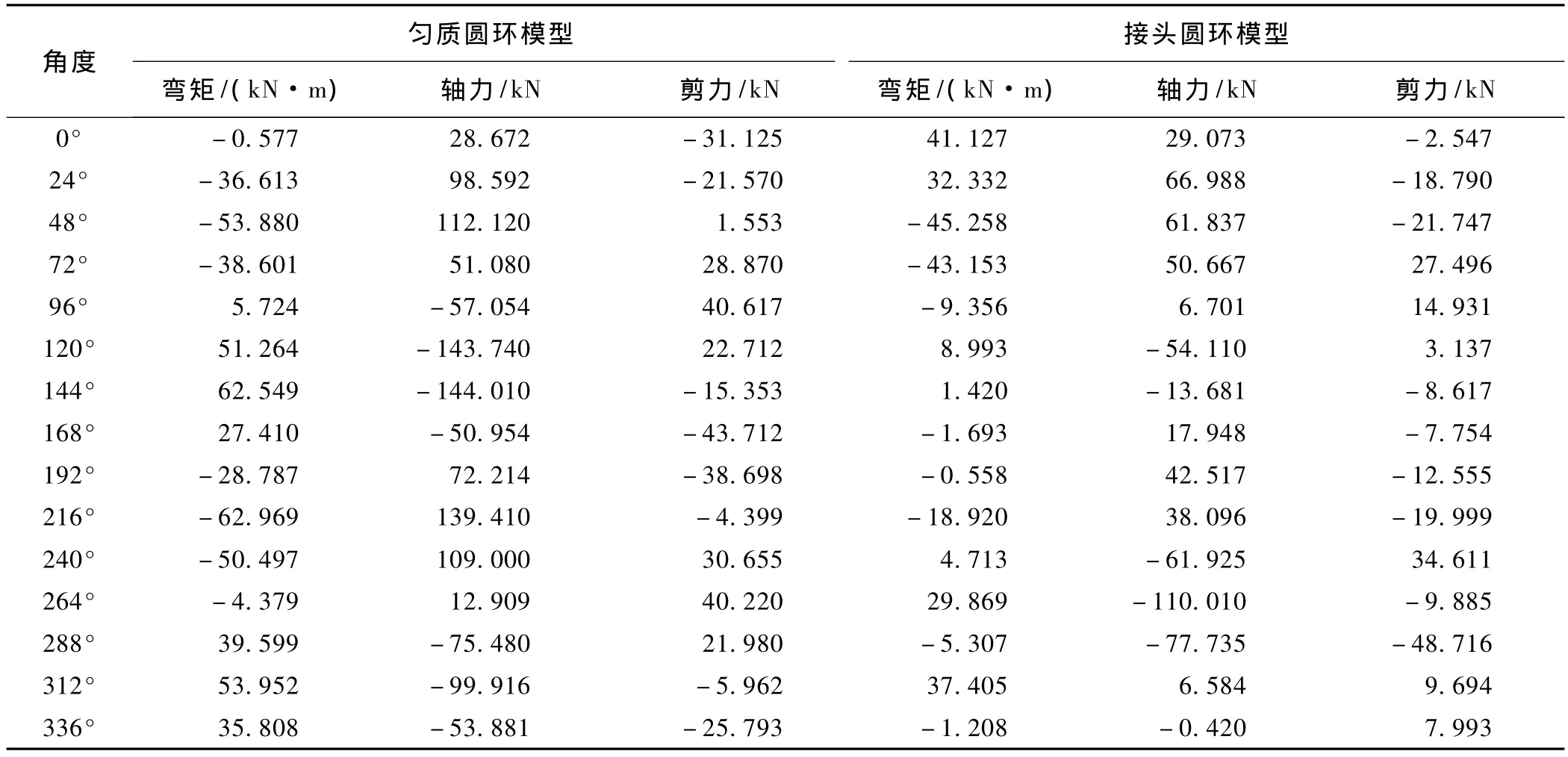
表1 两种模型地震荷载下反应位移法结果对比

从表1可以看出:通常情况下，按匀质圆环盾构隧道模型设计时所获得的弯矩、轴力和剪切力较接头圆环盾构隧道模型大，且弯矩、轴力和剪切力的分布规律明显。大致在与 x 轴成 45°、135°、225°、315°位置出现弯矩和轴力的局部最大值，而剪切力的局部最大值通常出现在 0°、90°、180°、270°附近。而接头圆环盾构隧道模型所计算出的弯矩、轴力和剪切力的局部最大值与封顶块的位置有关，因此需要结合盾构隧道施工时封顶块的所有不同位置开展计算分析，然后取其最不利内力进行抗震设计。对于接头圆环盾构隧道模型，由于接头分布不对称，其内力分布也表现出明显的非对称性，但接头处的弯矩通常较其它位置小。从表1中还可以看出，通常考虑接头效应时，弯矩和轴力的绝对值最大值比不考虑接头效应时要小，表明接头的存在削弱了盾构隧道的弯矩和轴力，这正是盾构隧道较为耐震的原因。

4 结语

反应位移法考虑了地层和盾构隧道的相互作用及盾构隧道与地层的动力追随关系，将地震荷载的作用简化为求解盾构隧道在地层弹簧约束下，受天然地层最大强制位移差及其对应时刻地层剪切力共同作用下的地震反应。不需要对盾构隧道进行连续介质地层结构模型的时程分析，简化了盾构隧道抗震分析工作量，是一种极具潜力的盾构隧道抗震设计方法。但在复杂地层条件下，其分析所需的物理力学参数，特别是地层自振周期、基岩速度反应谱以及地层弹簧刚度系数等参数准确获取较为困难，加之对地层强制变位余弦分布假设的近似性，这些因素在一定程度上制约了反应位移法在盾构隧道抗震分析中的应用。由于盾构隧道是由环向和纵向接头拼装而成的，因此，基于盾构隧道接头开展抗震设计是一种更加切合工程实际的分析途径，利用接头圆环模型分析的结果较匀质圆环模型更能表征结构的动力效应，值得在盾构隧道的抗震设计中推广。今后业界应在反应位移法物理力学参数的准确获取以及反应位移法与盾构隧道接头相互结合上开展更加广泛的工作，以推动反应位移法在盾构区间隧道抗震分析中的应用。

［1］关宝树，杨其新.地下工程概论［M］.成都:西南交通大学出版社，2001.

［2］黄先锋.地下结构的抗震计算—位移响应法［J］.铁道建筑，1999(6):3-6.

［3］边 金，陶连金，张印涛，等.地下结构抗震设计方法的比较与分析［J］.现代隧道技术，2008，45(6):50-55.

［4］刘如山，胡少卿，石宏彬.地下结构抗震计算中拟静力法的地震荷载施加方法研究［J］.岩土工程学报，2007，29(2):237-242.

［5］川岛一彦.地下构造物の耐震设计［M］.日本:鹿岛出版株式会社，1994.

［6］HE CHUAN，KOIZUMI ATSUSHI.Study on seismic behavior and seismic design methods in transverse direction of shield tunnels［J］.Structural Engineering And Mechanics，2001，11(6):651-662.