Khan Khwar电站竖井式厂房开挖过程仿真模拟

鲁永华 任智锋 顾小兵 郭西方

巴基斯坦Khan Khwar电站主厂房位于印度河与KaraKoram主干公路之间的小山包处。主厂房地面高程略高于厂区地面高程,为586.0m。主厂房长50.7 m,宽19.6m,总高度43.70m,其中地面以上高度为16.00m,地面以下深28.0m。主厂房内布置2台混流式机组。2台水轮发电机安装在竖井内,竖井长28.25m,宽22m,两端为半径11m的圆弧段。场区及竖井开挖前、后地形见图1。

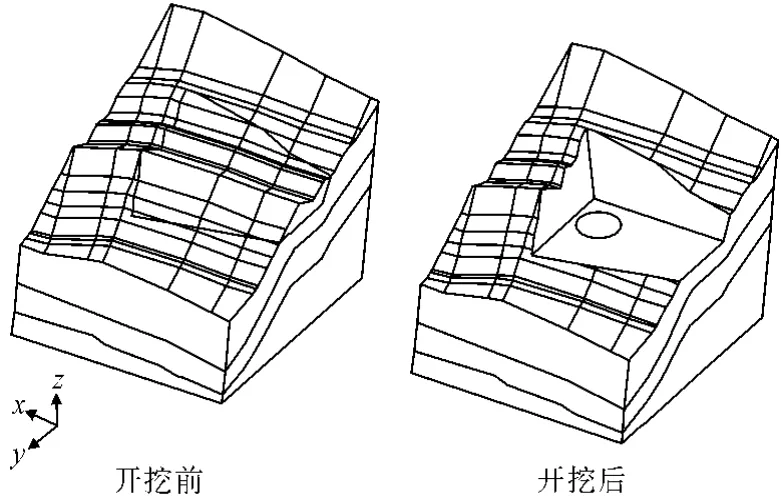
图1 竖井厂房厂址地形地质

1 工程地形、地质情况

电站场址位于印度河右岸坡脚地带,为斜坡地形,坡度 15°～20°,并有一小山包,地面高程580～605m。电站厂房位于小山包处,厂区基岩裸露,出露地层为Besham组淡色花岗岩和花岗片麻岩,坚硬、致密,局部见有赤铁矿蚀变带,一般岩体完整性尚可。强风化深度18.5～19.2m,弱风化深度31.1～40.7 m。地基岩石坚硬致密,强度、承载力高,强风化带深度大,开挖竖井式电站基础基本可坐落在弱风化岩体上。

2 计算内容及目的

对电站厂区及厂房竖井的分步开挖过程进行仿真模拟:模拟初始地应力场,为后续开挖计算提供初始计算条件;了解各步开挖后岩体变位、应力、应变和岩体塑性区的分布及范围;对各步开挖后围岩的稳定进行分析评价;若岩石失稳或塑性区范围过大需采取喷锚等工程措施进行处理时,模拟处理效果;根据分析成果为设计提供合理化的建议。

3 计算模型及计算方法

3.1 计算模型

根据厂区地形、地质特征和竖井式厂房及场区的开挖设计,建立三维实体模型,岩石材料按照强风化、弱风化、微风化地质分界线分为3层,分别赋予相应的物理、力学指标。计算模型在水平 x、y向长度均取椭圆洞室相应轴长的7倍;垂直方向上:竖井上部为实际地形特征,竖井底板以下的深度取竖井深度的3倍。模型底面固结,侧面约束水平向位移。

为较真实的模拟厂房竖井开挖过程,岩石采用弹塑性非线性材料模拟,弹塑性材料采用Drunker-Prager(D-P)本构模型。计算单元采用六面8节点Solid45实体单元。Drucker-Prager材料数学本构模型采用的是相适应的流动法则,并且认为其具有理想塑性屈服特征。计算中采用各类岩石物理、力学指标如表1所示。

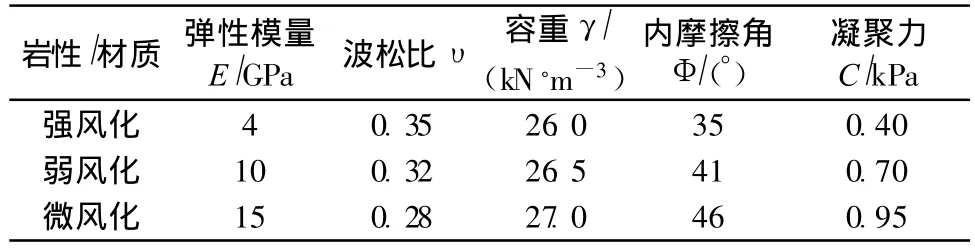
表1 岩石物理、力学指标

3.2 分步开挖过程仿真模拟

竖井开挖仿真模拟中,分析模型的质量分布状态不断变化,从而导致模型的刚度分布、边界条件等也相应改变,模拟难度较大,分析中借助ANSYS有限元分析系统提供的单元生死技术(Element Birth and Death),实现厂房场区及竖井分步开挖、衬砌的仿真模拟。

依据场区及竖井开挖的施工顺序,分以下计算步骤计算。

(1)对计算模型加载重力场作用,进行开挖前岩体初始应力场的模拟。

(2)对高程586.0m以上的厂区进行开挖。

(3)开挖高程586.0～581.0m间竖井。

(4)开挖高程581.0～576.0m间竖井。

(5)开挖高程576.0～571.0m间竖井。

(6)开挖高程571.0～566.0m间竖井。

(7)开挖高程566.0～561.0m间竖井。

(8)开挖高程561.0～558.3 m间竖井,竖井开挖完成。

在(2)～(8)计算步中,如发现局部岩石失稳或塑性区开展过大,记录其位置,建议设计对其进行喷锚处理,并模拟处理后效果。

4 一些问题的处理方法

4.1 地应力问题

岩体中的初始地应力由多种因素产生,工程岩体中地应力主要来源于地质构造和地球重力场的作用,大小主要取决于上覆岩层的重量、构造作用的类型、强度和持续时期的长短等。根据部分工程实测资料的分析,初始地应力常具有以下规律。

(1)一般情况下岩体中的初始应力场多是三向不等压的空间应力场,最大水平主应力大于垂直应力,最小水平主应力的数值则变化较大。

(2)初始应力的大小、方向与地质构造有着密切关系。一般位于活动断层的拐弯或交叉处的断裂构造会产生较大的应力集中,其它部位的断裂构造反而引起应力释放。

(3)坚硬完整的岩体内可积聚大量应变能,形成较高的初始应力,软弱破碎岩体中积聚的应变能不大,初始应力较低。脆性、高强度的岩体中往往积聚较大的初始应力。

(4)岩体上覆岩层的重量是形成岩体初始应力的基本因素之一,一般认为,岩体垂直初始应力基本上与上覆岩体的重量(γ H)相等。

(5)地形、地貌对初始应力有一定的影响,地形被切割后必然引起应力重分布。

Khan Khwar电站竖井式厂房位于一小山包处,山包位于印度河右岸坡脚地带,在KKH公路与小山包之间有一深槽,山包另外两侧地势较为平缓。考虑场区的地形、地质情况,结合地应力以上分布特征可推测电站厂址部位构造应力不大,初始地应力以自重应力场为主,计算中只考虑重力场引起的地应力。

4.2 加固措施的模拟

厂房竖井的开挖模拟依据实际施工过程分步进行,在各步计算中,若竖井围岩失稳或出现较大塑性区(岩石失稳表现为计算不收敛),可采用超前小导管注浆、喷锚等措施对其进行加固处理。锚杆的主要作用并非其自身强度对整体刚度矩阵的贡献,因为在整个体系中,锚杆刚度和周围岩体的刚度相比是微不足道的,喷锚的的实际作用是在施工过程中及时加固岩体、限制塑性区发展,维持岩体的连续性和完整性,从而能够很好地起到自撑作用。若计算中结果显示需对竖井围岩进行喷锚等工程措施处理,则采用提高处理部位岩体 C、Φ值的方法模拟计算。根据国内外研究成果及现场经验,锚固部位围岩参数中的C、Φ值能提高20%～30%。

5 计算成果及分析

5.1 初始地应场结果及分析

依据前面假设,对模型加载重力场作用得到初始地应力场,开挖前竖井中心线上各点三向应力结果见图2。

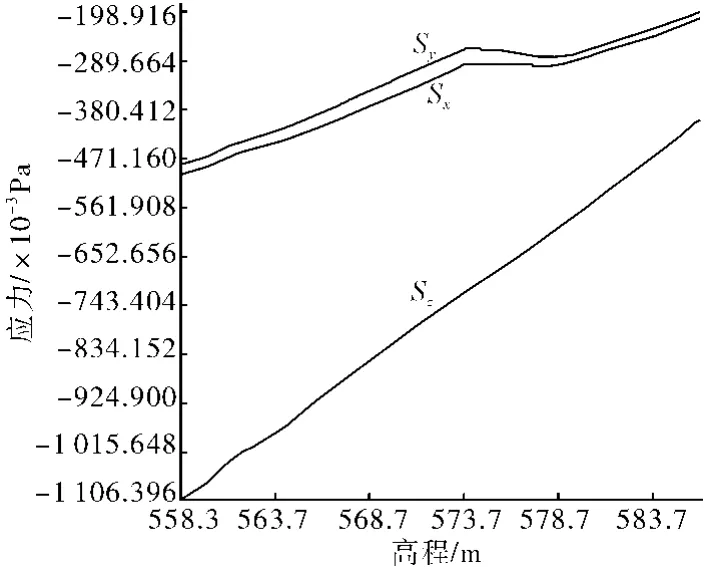
图2 开挖前竖井中心线上各点三向应力

由图2得出以下结论。

(1)大部分区域,尤其非岩层交界面,岩体的初始应力符合自重应力场的分布规律,各向应力均为压应力,在靠近地表处的压应力较小,随着深度的增加,压应力逐渐增大,竖向压应力与Sz=γ H的规律大致相符。

(2)同一高程面上各点压应力分布规律基本上反映了上部地形、岩性特征,上部地势较高,岩石容重较大的部位,压应力较大。

(3)由竖井中心线上各点三向应力对比关系可以看出,侧压力系数K0基本与经验关系式K0=υ/(1-υ)一致(υ为岩石泊松比),水平方向上压应力Sx略大于Sy,主要为场区地形特点所致。

(4)在图2中Sx、Sy出现一近似水平段,这是因在此高程范围内为岩层分界线,岩层走势起伏、岩性变化所致。

5.2 竖井开挖后成果及分析

5.2.1 井壁位移

竖井开挖后井底位移见图3,井壁位移见图4。

图3 竖井开挖后井底竖向位移(单位:mm,竖直向上为+)

图4 竖井开挖后井壁径向位移(单位:mm,向内收敛为-)

由计算结果可以看出。

(1)由于竖井及场区开挖的卸载作用,井壁、井底均发生不同程度的向上的竖向位移,以井底平面为大,井底中部的竖向位移为1.00mm。

(2)竖井开挖后,井壁发生向内的径向位移,竖井下部的径向位移较小,中部和上部较大,这主要是因为下部井壁压重较大、岩石工程性能指标较优所致。总的看来,径向位移较小(最大位移0.12mm),说明设计选用竖井断面形式较优,成拱效应较明显。

(3)井壁的径向位移在各高程断面上分布不均匀,这主要是由于地形高低起伏、岩层变化、竖井顶部各部位开挖卸载程度不同造成的。

5.2.2 井壁应力

竖井开挖后井壁环向、竖向应力分别见图5、6。

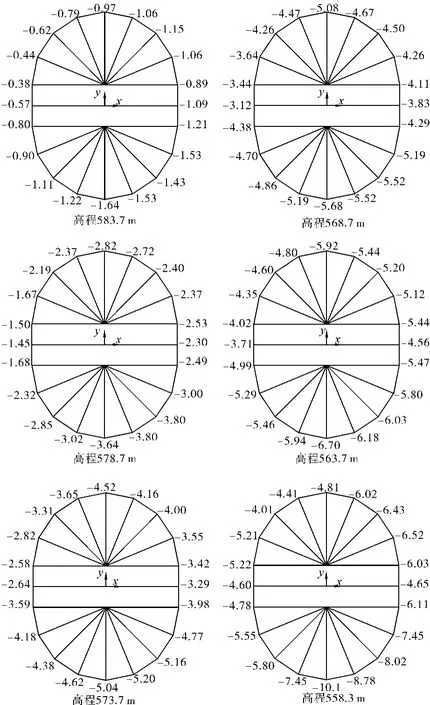
图5 竖井开挖后井壁环向应力图(单位:105Pa,-为受压)

由计算结果可以看出。

(1)井壁各高程环向、竖向应力均为压应力,无拉应力。

图6 竖井开挖后井壁竖向应力图(单位:105Pa,-为受压)

(2)井壁的环向、竖向应力均随深度的增加而增大,最大值出现在井底高程,分别为1.01mPa和1.71mPa,小于岩石的允许抗压强度3～5MPa。

(3)井壁的竖向、径向应力在各高程断面上分布不均匀,主要是地形高低起伏、岩层变化、竖井顶部各部位开挖卸载程度不同造成的。

5.2.3 井壁塑性区

竖井开挖后井壁岩体塑性应变等值线见图7,高程583.0m平面塑性应变等值线见图8。

由图7、8可知:塑性区主要出现在竖井上部高程580.0～586.0m之间,平面上塑性区在靠印度河位置较发展,距井内壁约6.0m,井壁最大塑性应变6×10-5,综合考虑竖井周围塑性区的分布及塑性应变的大小,竖井围岩稳定。

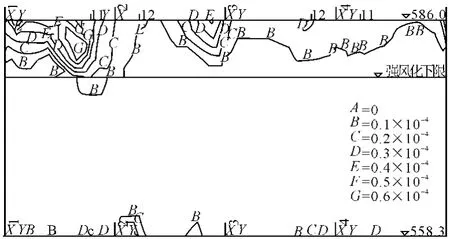
图7 井壁岩体塑性应变等值线图

图8 高程583.0m平面塑性应变等值线图

6 结论及建议

从计算成果看,场区开挖及厂房竖井各步开挖过程中,围岩中未出现较大的拉应力及塑性开展区,总体而言,竖井围岩是稳定的。井壁处岩石开挖时建议采用预裂爆破,以减小爆破的影响范围和提高井壁的平整度。本计算根据强风化、弱风化、微风化地层分界线将岩石分为3种弹塑性材料,每种岩石均视为均一、各向同性,计算结果亦是在此基础上取得,考虑到地质情况的复杂性和多变性,施工过程中应做好监测工作,以便根据现场实际情况,及时采用相应的处理措施。