利用期刊下载次数估计后期被引次数的研究

●郭 强，赵 瑾，刘新新，王玲玉，贾光耀

（1.郑州大学 信息管理系，郑州 450001；2.中国人民解放军炮兵学院 军事运筹教研室，合肥 230031）

由于下载次数与被引次数之间的关系体现了同一性与差异性的对立与统一，那么是否可以利用这种同一性来对被引次数进行估计或是预测，毕竟与被引次数相比，下载次数能够视为对期刊或论文等评价对象的学术价值的先期反映，由此，如果能够从前期的下载次数得到后期的被引次数，并且进一步得到后期的诸如期刊的影响因子等综合指标，则对于科学评价的提前会有一定的意义。

1 总量估计

如果选取期刊作为考察对象，并利用下载次数来对期刊在某一年的总的被引次数进行估计，那么需要考察期刊的下载次数与被引次数之间的相关性以及相关的程度。由于已有经验考察的结果往往显示为期刊的下载次数与被引次数作为随机变量均服从负指数分布，尽管经验考察在处理变量分布规律时会有其方法上的局限性，但是这种经验结果至少意味着，需要考虑简单相关分析对于下载次数与被引次数的适用性，特别是在推断统计考察上，毕竟简单相关要求考察变量均服从正态分布。这样，对于下载次数与被引次数相关程度的考察则需要采用适用于非正态分布情形的等级相关，［1］或者可以更为直观地，如果不涉及具体的推断统计，则至少回归分析中的最小二乘法以及决定系数仍然可以利用，由此来近似地考察该两变量之间的统计相关性。因为CNKI镜像站版的引文数据库能够提供其入库期刊的逐年下载次数以及被引次数，所以在这里将其作为数据来源，首先以《情报科学》为例，并对该期刊的前期下载次数与后期被引次数进行线性回归，能够得到不同时间间隔的决定系数如图1所示，数据统计时间为2009年8月。

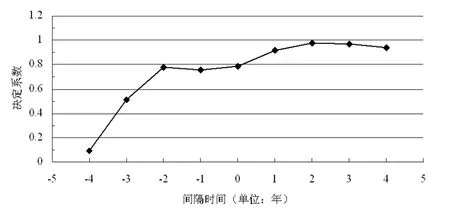
图1 下载次数与被引次数线性回归的决定系数随时间间隔的变化关系

在图1中，考察期刊的逐年下载次数列与其后期相隔n年的被引次数列，对由此形成的下载次数与被引次数对的样本集合进行线性回归，其中间隔时间n为正数时表示被引次数较下载次数为后期，取负时则表示被引次数为前期，考察时段为2000年至2007年，能够注意到当n取2时决定系数为极大，达到0.9808，由于此处的决定系数反映了用线性关系进行拟合时所得回归关系对总变异的贡献程度，所以意味着下载次数列与后期相隔两年的被引次数列高度线性相关，且回归方程为c=0.0613d+304.55，其中c与d分别为期刊的被引次数与下载次数。以上能够说明对于样本集合而言，期刊的某年度下载次数与其后年的被引次数之间的确存在显著的直线相关，而且与其他的时间间隔相比，直线相关程度会相对较高，而这些情况在研究总体中是否存在还需要进行显著性检验，由于期刊某年度的下载次数或是被引次数均服从负指数分布，所以在考察总体相关系数的置信区间时不能采用适用于正态分布的估计方法，由此在这里不直接进行显著性检验，而是采取近似的经验考察，如果能够认为对于图书情报专业的期刊论文，作者从其对文献的下载到在最终成果中对该文献的引用，所需时长为两年较为符合经验认识的话，则期刊在某年度的总的下载次数与两年后该期刊的总的被引次数之间会具有较强的正直线相关性，从而可以在一定程度上认为研究总体也具有相应的特征，由此可以借助所得回归方程用期刊某年度的下载次数来对两年后的期刊被引次数进行估计，例如由2006年的期刊下载次数可以得到期刊在2008年的总的被引次数为c1=0.0613×58636+304.55=3899，这与在2009年8月时所得数据3797较为吻合。

2 期刊被引次数的年代分布

假设期刊在某年度被引次数的年代分布规律为y（t）=C0［exp（-αt）-exp（-mt）］，其中C0、m、α均为待定常数，且m＞α，t为距离该考察年度的时间间隔，非负且单位为年，y（t）为在t间隔时长处的期刊被引次数，［2］则可以利用期刊的被引半衰期以及最大引文年限来对方程中的参数进行确定。CNKI镜像站版的引文数据库能够提供逐年的期刊被引总量以及相应的被引文献列表，由此可以对考察年度中不同年份被引文献的被引次数分别进行求和，将所得到的各年被引量按照文献出版年的降序进行排列，并在此基础上求得期刊在该考察年度的累积被引次数以及相应的累积百分比，得到当累积百分比达到50%时的文献出版年份，或者说此时对应的累积被引次数达到了期刊在考察年度的被引总次数的一半，从而可以给出该出版年份与考察年度之间的期刊出版年数，并记与考察年度对应的期刊出版年数为1，由此得到期刊在考察年度的被引半衰期。另外，如果是以年作为时间单位来对期刊的被引次数进行统计，那么实际数据往往只能给出与50%的累积比重最为接近的文献出版年，所以此时的期刊被引半衰期通常是利用该出版年与相邻文献出版年的累积百分比来进行线性近似得到的，例如《情报科学》期刊在2007年的被引总频次为4051，由于在按文献出版年份降序排列的被引次数列表中，2004年对应的累积百分比为53.57%，与其余年份相比，此时的累积比重与50%最为接近，于是该期刊在2007年的被引半衰期为 3+（50-36.07）/（53.57-36.07）=3.80年，其中36.07%为2005年对应的累积百分比，相类似地，能够得到该期刊从2000年至2007年的被引半衰期如图2所示。还需要指出，对于原始数据中出现的在考察年度引用其后期文献的记录，比如在2001年引用了2002年的期刊论文，这种情形没有考虑在内，毕竟在这里考察的是期刊的被引半衰期。

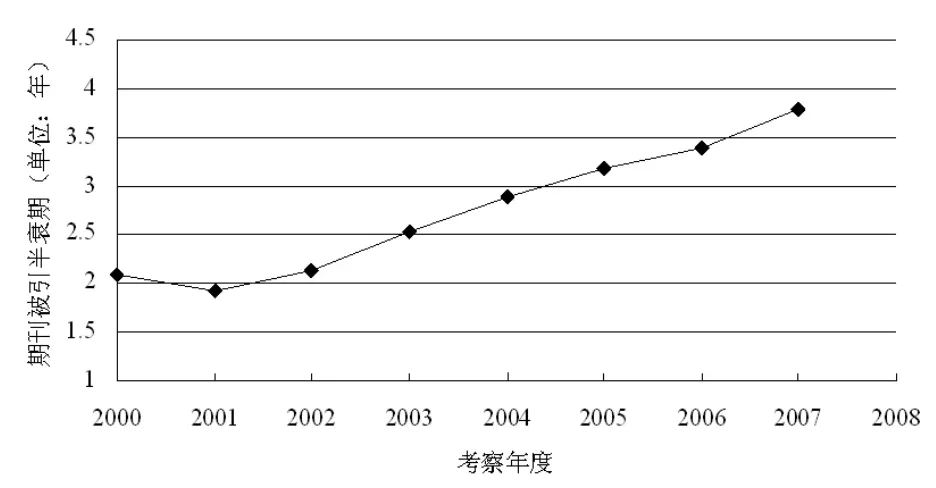
图2 《情报科学》期刊的逐年被引半衰期

在图2中，从直观上能够注意到自2001年起期刊的被引半衰期逐渐增加并且具有线性增长的趋势，被引半衰期的上升往往意味着出版年份更为靠前的过刊内容会得到更多的被引次数。究其原因，一方面是由于期刊论文整体学术价值的提升，出版时间与考察年度间隔较长的过刊文献，在考察年度仍然具有较高的参考价值或者是学术影响力，所以文献的老化速率会有所减缓；另一方面则可能是由于期刊论文中的理论以及基础应用性研究所占比重的增加，该类型文献与应用或实证性研究相比通常会具有较长的时效性，毕竟后者往往需要建立在即时的实证数据基础上，或者是对某个特定领域的应用考察，由此与理论研究等相比可能并不具备更强的一般性以及适用性，从而文献被引频次的年代分布以及文献的老化速率等也会受到影响；第三，更为重要的是，随着图书情报专业的发展，其专业期刊的影响力也在逐渐增强，特别是该领域中先期可能未被发现的学术价值如今能够逐步得以体现，与此相对应地有该类文献被引次数的增加以及老化速率的下降，从而期刊的半衰期能够有所延长。

如果可以假设上述引起期刊被引半衰期增长的种种原因依旧存在，并且期刊文献的学术价值随出版时间保持平稳上升，同时诸如偏理论文献的比例等期刊特色能够维持不变或者是随时间平稳增加（改变），进一步假设相同的文献学术价值的增加所对应的期刊半衰期的上升也相同，当然两者增加的幅度会有所差异，也即假设文献整体的学术价值与期刊被引半衰期之间为线性关系，并近似认为其余的因素对于被引半衰期也具有类似的线性影响。再假设所有因素的综合影响为各单个因素的影响的线性叠加，则能够认为各因素对于期刊被引半衰期的综合影响为线性，或者是被引半衰期与所有影响因素之间的关系为多元线性关系，从而有半衰期会随时间线性增长（变化）。需要指出，上述各假设从直观上均具有一定的合理性。

另外，如果再考虑到期刊规模的改变对于文献整体价值乃至对半衰期的影响，毕竟载文规模的变化可能会引起稿件刊用标准的调整，这其中既存在由于稿件数量与质量的同时上升，则稿件录用标准可能会相应地维持不变甚至会有所上调，同时也存在着文献整体价值下降的情形，所以从直观上并非是随着期刊规模的增加，期刊文献的整体价值就会减少，两者之间的线性关系并不显然。并且如果能够认为期刊载文规模以及稿件的数量与质量同为稿件刊用标准的主要决定因素，那么这些因素之间的相互作用从直观上可能会带来期刊规模与刊用标准之间的非线性关系，从而期刊规模与文献整体价值以及被引半衰期之间的联系也非线性。由此在上述假设的基础上，被引半衰期与包括期刊规模在内的影响因素之间不成多元线性关系，这样，即便期刊的规模会随时间发生线性变化，期刊的半衰期与时间也为非线性关系，所以为简单计算，可先不考虑期刊规模的影响，但前提是期刊规模在考察时段内随时间不会有明显的改变，从而可以按常量来处理，保证期刊的被引半衰期随时间的线性变化具有一定的合理性，例如在图3中，《情报科学》期刊自2000年改为月刊后至2008年的这段时间内，期刊年度载文量随时间的变化相对较为平稳。

那么，在期刊半衰期与时间之间近似满足线性关系的基础上，可以对图2中的数据进行线性拟合来对期刊的被引半衰期进行估计，自2001年起的线性回归方程为h=0.3136t-625.66，其中h和t分别期刊的被引半衰期与考察年度，且判定系数为0.9939，由此可得2008年度的被引半衰期为4.05年，可以利用期刊在2008年的实际被引数据对该估计值进行检验，所得结果为4.07年，其中数据统计时间为2009年8月，从而能够从侧面反映上述假设具有一定的合理性。

《情报科学》期刊的最大引文年限能够在上述确定被引半衰期的过程中直接得到，同样利用CNKI镜像站版所提供的该期刊在考察年度的被引文献列表，将列表中各文献的被引次数分别按照文献出版年进行求和，则能够得到该期刊的被引次数在考察年度的出版年代分布，根据被引次数最多的文献出版年与考察年度的时间间隔，可得该期刊在各考察年度的最大引文年限如图4所示，其中记考察年度自身所对应的时间间隔为1年。

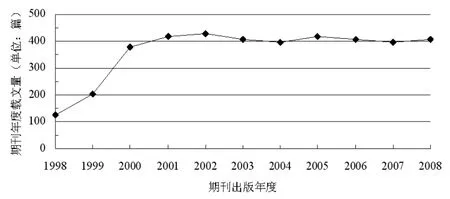
图3 《情报科学》期刊的年度载文量

图4 《情报科学》期刊的最大引文年限随时间的变化情况

和被引半衰期相比，期刊的最大引文年限更多地是与期刊被引次数的绝对量相对应，毕竟被引半衰期是由被引次数的累积百分比来得到的，于是相对量与绝对量之间的差异会使得该两老化指标随时间的变化情况也会有所不同，当最大引文年限小于被引半衰期时，从直观上会有两指标之间的差异越大，则从被引峰值处向前回溯，被引次数的递减速率相应地会有所减小，所以该两指标间的差异能够在一定程度上反映被引峰值过后的期刊文献老化状况或是程度，而对于最大引文年限大于被引半衰期的情形，则意味着从被引峰值处起期刊被引次数的快速下降。在图5中，k为对考察年度中引文峰值至被引频次首次为零处的被引次数进行线性最小二乘拟合来得到，且各年度的决定系数均大于0.93，如果不严格地，能够注意到期刊半衰期与最大引文年限的差值d和递减斜率k的历时变化具有一定的同步性。

既然半衰期与最大引文年限的差异能够作为对被引峰值过后的文献老化状况的反映，那么如果能够认为后者随时间进行线性变化具有一定的合理性，并且进一步认为，由于期刊的被引半衰期从2001年起随时间线性增长，所以被引峰值过后的文献老化程度会随时间线性下降，相应地，该两老化指标之间的差异也会随时间线性增长。由于图5中从2003年开始，在两指标的差值随时间线性增长的同时，图4中的最大引文年限会保持不变，所以在该差值继续维持线性增长的情况下，能够近似认为最大引文年限也不会发生变化。

图5 k与d随时间的变化情况

另一方面，最大引文年限与被引半衰期相比具有较大的惯性，除了在图2与图5中能够对此有所体现之外，还可以利用被引次数的年代分布规律y（t）=C0［exp（-αt）-exp（-mt）］来进行大致的考察，其中m＞α且均为正数，对 y（t）求导可得 y'（t）=C0［（-α）exp（-αt）-（-m）exp（-mt）］，则函数y（t）的驻点为t1=［ln（m/α）］/（m-α），由于

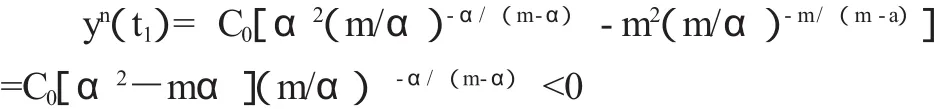
所以函数y（t）在t1处取极大值，也即t1与最大引文年限相对应，于是期刊的最大引文年限在这里仅与m与α两个参数有关。对于期刊的被引半衰期，如果取时间为连续变量，并设期刊的被引半衰期为t2，则有

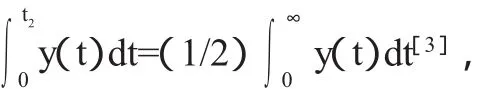
这里的t2的取值除了与m与α有关之外，还受到参数也即期刊在考察年度的被引总频次的影响，所以从直观上能够近似认为最大引文年限的惯性相对较强。

考虑到以上两点，在这里仍取2008年的期刊最大引文年限为3年，实际上根据2009年8月的期刊被引数据，能够得到2008年的k值与d值分别为-88.667以及1.07，并有期刊的最大引文年限为3年，由此，上述讨论具有一定的合理性。

此时尝试对2008年《情报科学》期刊被引次数的年代分布规律进行确定。由于该期刊在2008年的被引总次数、被引半衰期以及最大引文年限的估计值分别为3899次、4.05年以及3年，那么如果取时间为连续变量，则有

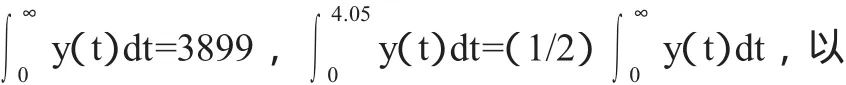
及y'（t）|t=3=0，将y（t）=C0［exp（-αt）-exp（-mt）］带入，以确定参数C0,α以及m，由此2008年的年代分布曲线也能够确定下来。从该方程组可以得到：与线性方程组相比，非线性方程组的解集情况会相对较为多样，在不同的区域内，可能会有唯一解、多个解或是无穷多组解的情形出现，因此可能会涉及到对具有实际意义的解的判别标准，同时对于非线性方程组的求解过程，在通常情况下也并不具有通用的方法。所以一方面可以注意到在上述方程组中所存在的对称性并对其进行利用，特别是前两个等式，分别构造函数：

对应相同f（x）值的m与 α，如果同时满足 g（m）=g（α），则为该非线性方程组的解，相应地，常数C0也可以得到，或是从直观上，f（x）与g（x）的函数曲线如图6所示。在图6中，以水平直线上下平移，并设在坐标原点以下该直线与函数f（x）的两个交点分别为A'与B'，如果存在这样的两点使得g（xA'）=g（xB'），则该两点的横坐标即为所求得m与α，其中m＞α。另外，图6中的点A与点B为曲线f（x）与g（x）的交点，如果该两点对应的函数值相等，也可以有m=xB以及α=xA，但实际上xA=0.32，f（xA）=-0.7，xB=0.51，f（xB）=-0.734，函数值有一定的差距，并且经迭代检验，m=0.51，α=0.32并不稳定，所以该数对并不是最终所求。

另一方面则可以采取迭代法，将上述方程组化为迭代方程，并给定初值以及精度要求进行迭代，但是迭代的过程与迭代结果的敛散性均与初值的选取有关，对于解的情况较为复杂的方程或是方程组而言，需要大致了解所求参数m,α以及C0的取值范围，从而有可能通过迭代进行确定。由此对于上述方程组的求解还需做进一步的探讨，目的是希望得到对于该类方程组的一般解法，毕竟如果文中的估计方法可行的话，则所得方程组的形式包括对称性等都会保持不变。

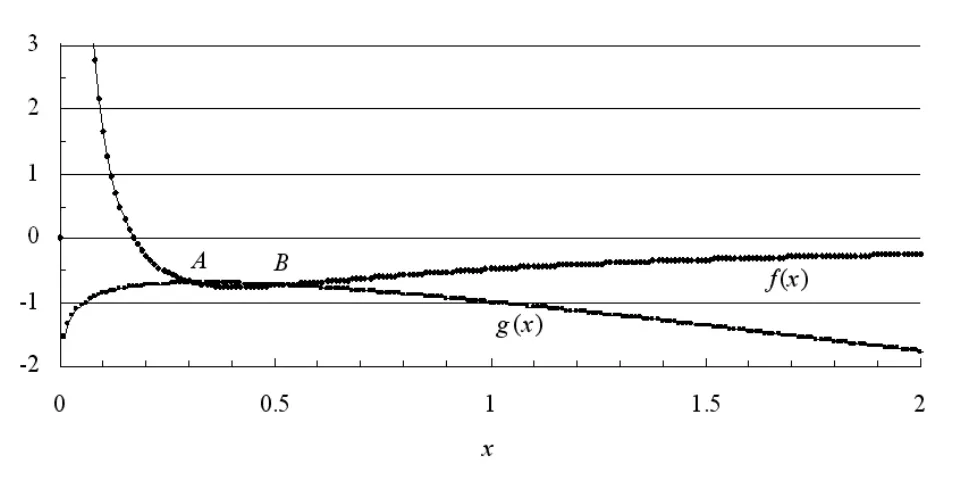
图6 函数f（x）与g（x）的曲线图

3 讨论

假设能够得到《情报科学》期刊在2008年的被引次数年代分布为y1（t），则该期刊中出版年度为2006与2007年的文献在2008年的被引次数分别为y1（3）与y1（2），由此根据期刊影响因子的定义，可得期刊在2008年的影响因子为［y1（3）+y1（2）］/［N（2006）+N（2007）］，其中N为期刊在相应年度的载文量。这样可以利用期刊在2007年之前（包括2007年）的下载与被引数据来对期刊在2008年度的影响因子进行估计。更进一步地，如果可以粗略地认为期刊的被引半衰期以及最大引文年限的惯性足够大，从而使得该两变量的变化趋势能够维持其后两年近似不变，则利用2006年之前（包括2006年）的下载与被引次数也可以进行大致的估计。

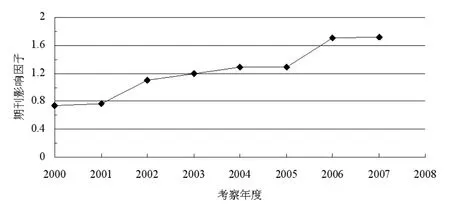
图7 《情报科学》期刊的逐年影响因子

需要指出，在这里没有采用对期刊的过往影响因子直接进行拟合来估计其后期取值，原因是由于根据图7中期刊影响因子的历时变化所呈现出来的趋势，采取线性拟合或是非线性拟合从直观上并不显然，更何况由于数据量较小，所以还需要考虑到所得数据中随机因素的影响。实际上，按照2009年8月的被引数据能够得到期刊在2008年的影响因子为1.465。另外，不同的数据源所提供的期刊被引次数会有差异，毕竟其入库期刊以及引用文献的统计范围会有所不同，所以图7中的期刊影响因子可能与其他的统计值会有出入，但是这并不影响文中估计方法的可行性。

对于期刊的被引次数以及影响因子的置信区间，则由于下载次数与被引次数均服从负指数分布，所以可能会涉及到负指数分布变量的平方和所服从的分布规律等，因此对置信区间的确定还需做进一步的探讨。其次，由于期刊在某年度的被引次数与其两年前的下载次数之间存在高度的正相关性，所以可以利用后者来对前者进行估计，但实际上由图1可以注意到期刊在某年度的被引频次与其前四年的下载次数之间都分别具有较高的线性相关性，由此对被引次数进行估计时，是否能够建立期刊在某年度的被引次数与过往各年度下载次数的多元线性关系，而这与直观认识也较相符合。另外，以上对被引次数以及影响因子的估计是建立在线性假设的基础上，从而有其局限性，同时，数据库的扩容与更新等往往意味着数据统计范围的改变，从而使得期刊的被引数据会发生变化，所以在得到影响因子的估计值时需要指出原始数据的统计时间。

［1］庞景安.中文科技期刊下载计量指标与引用计量指标的比较研究［J］.情报理论与实践,2006,29（1）∶44-48.

［2］ Aurel Avramescu.Actualityand obsolescenceof scientificliterature［J］.Journal of the American Society for Information Science，1979，30（5）：296-303.

［3］ Leo Egghe.Atheory of continuous rates and applications tothe theory of growth and obsolescence rates［J］.Information Processing and Management，1994，30（2）：279-292.