基于CSA算法的快堆堆芯燃料管理研究

杨晓燕,徐 銤,王 侃,胡永明,李泽华

(1.清华大学工程物理系,北京 100084;2.中国原子能科学研究院,北京 102413;3.清华大学核能与新能源技术研究院,北京 100084)

在第四代反应堆堆型中,快堆凭借其固有安全、增殖以及可嬗变的优点占据很重要的位置。随着核电的发展,从铀资源的有限性以及先进的第四代反应堆发展来看,快堆有着很好的发展前景,国内第一座实验快堆也已临界。因此,快堆的堆芯燃料管理优化也就有着很重要的意义。

堆芯燃料管理优化就是在满足核电站所有的安全和工程限制条件下,对燃料循环做出决策,使核电站获得更好的经济效益。目前,国内对于压水堆的堆芯燃料管理已经有了一定的研究,而对快堆堆芯燃料管理的研究才刚刚起步,因此快堆堆芯燃料管理的研究可以参考压水堆堆芯燃料管理研究的经验和结果。

1 CSA算法简介

1.1 CSA算法原理与流程图

CSA(Character Statistic A lgorithm)算法是一种全局优化算法。它根据问题的特点,选取一些与目标函数全局性相关的量作为特征量,然后利用特征量在优化过程中的变化规律引导搜索优化解。CSA算法的原理如图1所示,即找出基于自变量x的特征量Gi(x),使得多极值问题简化为单极值问题,并利用特征量Gi(x)在优化过程中的变化规律引导整个优化过程。该算法用于堆芯燃料管理的流程图如图2所示。

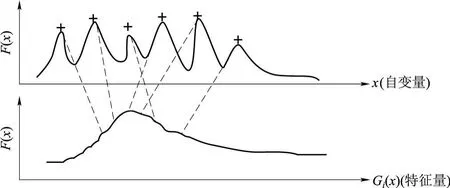
图1 CSA原理图Fig.1 Princip le of CSA

图2 CSA流程图Fig.2 Flowchartof CSA

目前,CSA算法已经可以很好地用于压水堆的堆芯燃料管理[1]。

1.2 特征量与目标函数

在CSA算法优化过程中,特征量是用于进行特征曲线的统计以引导优化搜索,目标函数是判断方案优劣的标准。因此,特征量与目标函数的确定是两个最重要的问题。

根据堆芯物理的基本知识可知,在堆芯燃料管理中,堆芯的相对功率分布非常重要。因此,在进行特征量的选取时,要尽量使得特征量与堆芯的相对功率分布密切相关。

根据反应堆k∞的定义,定义燃料组件(简称组件)k∞的概念。组件k∞是组件各项参数的宏观体现,与组件的相对功率有着很大的关系。CSA算法在压水堆堆芯燃料管理中的应用说明,组件的相对功率不仅与组件k∞有着很大的关系,与邻近位置处的组件k∞也密切相关[1]。因此,在压水堆的堆芯燃料管理中,特征量选取为组件k∞与邻近位置处的组件k∞的组合。组合方式如图3所示,为该位置组件与4盒周围组件的组合,记所选取的(i,j)位置的特征量为G(i,j),则：

在快堆的堆芯燃料管理中,借鉴压水堆燃料管理的经验,同样选取组件k∞的组合为特征量,由于快堆六角形组件的特殊性,组件组合时需要考虑到周围6盒组件,如图4所示。快堆在物理特性上与压水堆有着较大不同,在快堆中,堆内的能谱相对较硬,快中子的平均自由程较长,这些都会对特征量的选择带来影响。经过一系列的验证计算,以下的特征量可以较好地表示快堆的堆芯相对功率分布。如图5所示。

图3 压水堆1/4堆芯布置图Fig.3 1/4 core layout of PWR

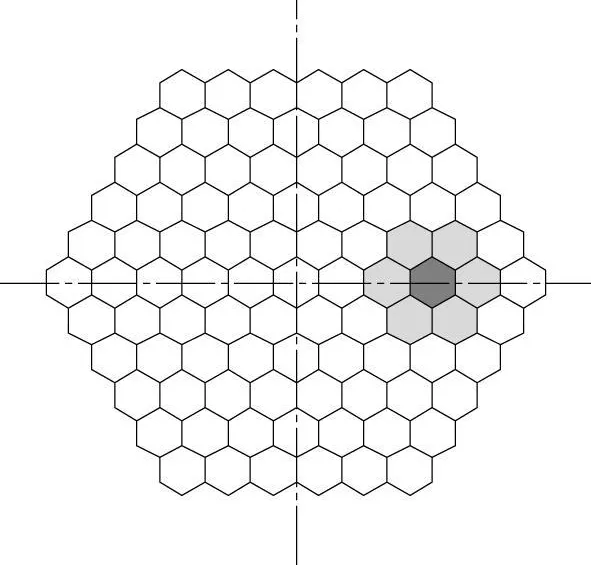
图4 快堆堆芯布置图Fig.4 Core layout o f fast reactor

图5 相对功率分布图Fig.5 Relative power distribution

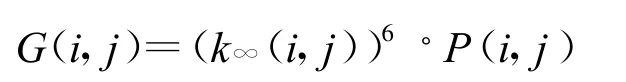
其中G(i,j)表示(i,j)位置处的特征量,k∞(i,j)表示(i,j)位置处的组件k∞,P(i,j)与组件所处的位置有关,通过计算得到。

图5中所采用的例题描述如2.2节所示,图中控制棒位置的相对功率分布值为0,因此,曲线在控制棒编号处被截断。图5显示,对于本文中的例题,在给定堆芯布置及组件参数的情况下,由特征量G(i,j)可以较好的构造出堆内的相对功率分布,该特征量的选取很合理。

由图2可知,特征量是用于特征曲线统计,以引导优化搜索方向。根据以上对特征量的讨论,可以选取每个位置处的G(i,j)为特征量,假设堆内有N个组件位置,则会有N条一维特征曲线。

堆芯燃料管理的目的就是在符合各种安全限值的情况下尽可能地提高经济性,因此目标函数包含两部分内容：一是想要实现的目标,二是约束条件,设约束条件的数目为M,则一般堆芯燃料管理的目标函数及约束条件如公式(1)所示。

通过对中国实验快堆CEFR以及其他大型快堆的分析,在快堆的堆芯燃料管理中,主要的优化目标为循环长度或者平均卸料燃耗,主要的限值为两个设计限值,即燃料最大卸料比燃耗和燃料棒最大线功率,则快堆堆芯燃料管理目标函数及约束条件如公式(2)。不论是循环长度的大小还是平均卸料燃耗的大小体现在堆芯的有效增殖因子keff上,因此,本文中的优化目标取为有效增殖因子keff。

本文的主要目的是研究在倒料的情况下,CEFR的卸料燃耗可以达到的深度,因此根据CEFR的设计文件,燃料最大比燃耗以及燃料棒最大线功率分别取为100 MW◦d/kgU和40 kW/m。

2 CSA算法用于快堆堆芯燃料管理

2.1 优化模型

中国实验快堆(CEFR)是我国第一座快堆,有完整的从首循环到平衡循环的各项参数以及整个换料方案,因此,选择CEFR为计算对象,对其平衡循环的换料进行优化计算。根据CEFR的平衡循环堆芯布置,可以得到简化的CEFR计算模型,符合1/3旋转对称,如图6所示。图6中每盒组件对应的数值为该组件在优化过程中所对应的编码位置。

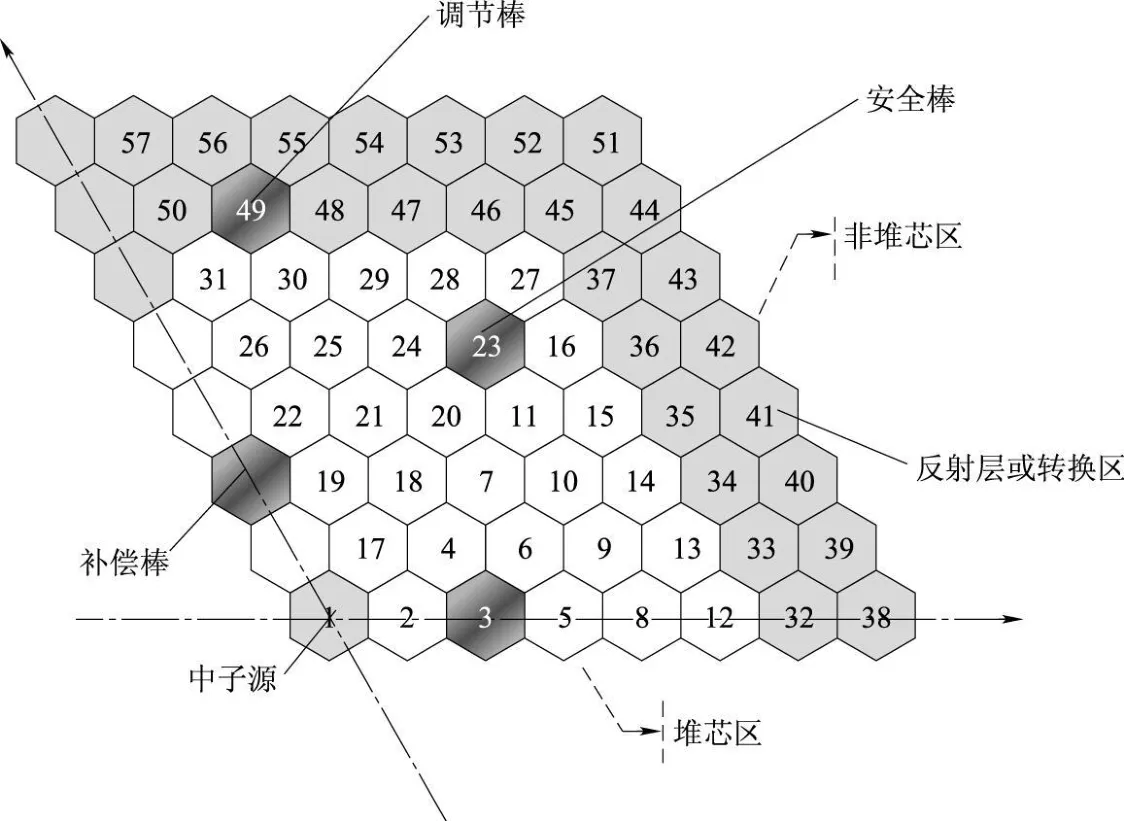
图6 CEFR优化模型Fig.6 CEFR op tim izationmodel

2.2 优化结果分析

本文中的优化为倒料优化,采用3批换料方式,样本大小为30,总方案数为2 000。本文给出优化末所得的最优方案的计算结果,为进行对照,也同时给出非优化的最优方案的计算结果,即随机产生2 000个方案,找出其中最优的方案进行对比计算。计算结果如表1所示。另外,在表1中也同时给出CEFR实际的平衡循环换料结果。

表1中优化以及非优化的结果是对相应的方案进行全堆迭代计算得到的结果,迭代的次数为批料数的2倍。

表1 计算结果分析Table 1 Analysis of optim ized and non-optim ized LPs

表1中的数据说明：①与CEFR现有的不倒料换料相比,进行倒料换料可以使得循环长度延长26 d左右,卸料燃耗大大加深,并且卸料燃耗更加平均;②优化结果与非优化的结果相比,进行优化获得了增加3 d的循环长度,将近1MW◦d/kgU的平均燃耗的加深,从这些数字上来说优化并没有得到非常大的效果,这主要是由于CEFR的特点决定的,CEFR是一个小型快堆,堆内组件数只有81盒,另外快中子的平均自由程很长,因此整个堆的泄漏较大,由不同的堆芯布置造成差别不如压水堆的大,优化的空间较小,这也是造成第三个方面内容的原因,然而在CEFR较小的优化空间下,优化的作用还是较明显的,这一点可以从图7看出;③在不同的堆芯布置下,堆芯的燃料棒最大线功率改变也不大。

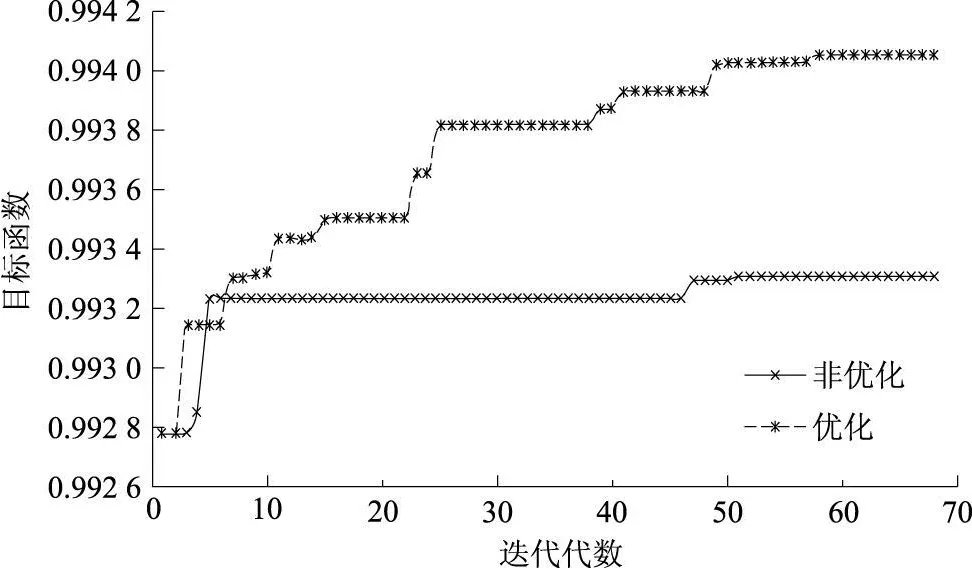
图7 目标函数的收敛曲线Fig.7 Convergence curve of the ob jective function

优化所得到的最优方案的布置图如图8所示,组件内的数字表示燃料所经历的循环数,0表示新燃料,1表示经历过一个循环的燃料,2表示经历过2个循环的燃料。

对于倒料优化而言,不考虑功率峰值因子的影响,要使有效增殖因子keff最大,最优的布置是从里到外依次为新燃料组件、经历过1个循环的燃耗组件,最外圈是燃耗最深的燃料组件。表1的数据显示,对于CEFR,不同的堆芯布置并不会对燃料棒最大线功率特别大的影响,那么最优布置应该是从里到外燃耗依次加深。在图8中,除了有1盒新组件出现在以中子源为中心的第4排外,其他新燃料组件都在1到 3排,经历过1个循环的燃料组件也是如此。

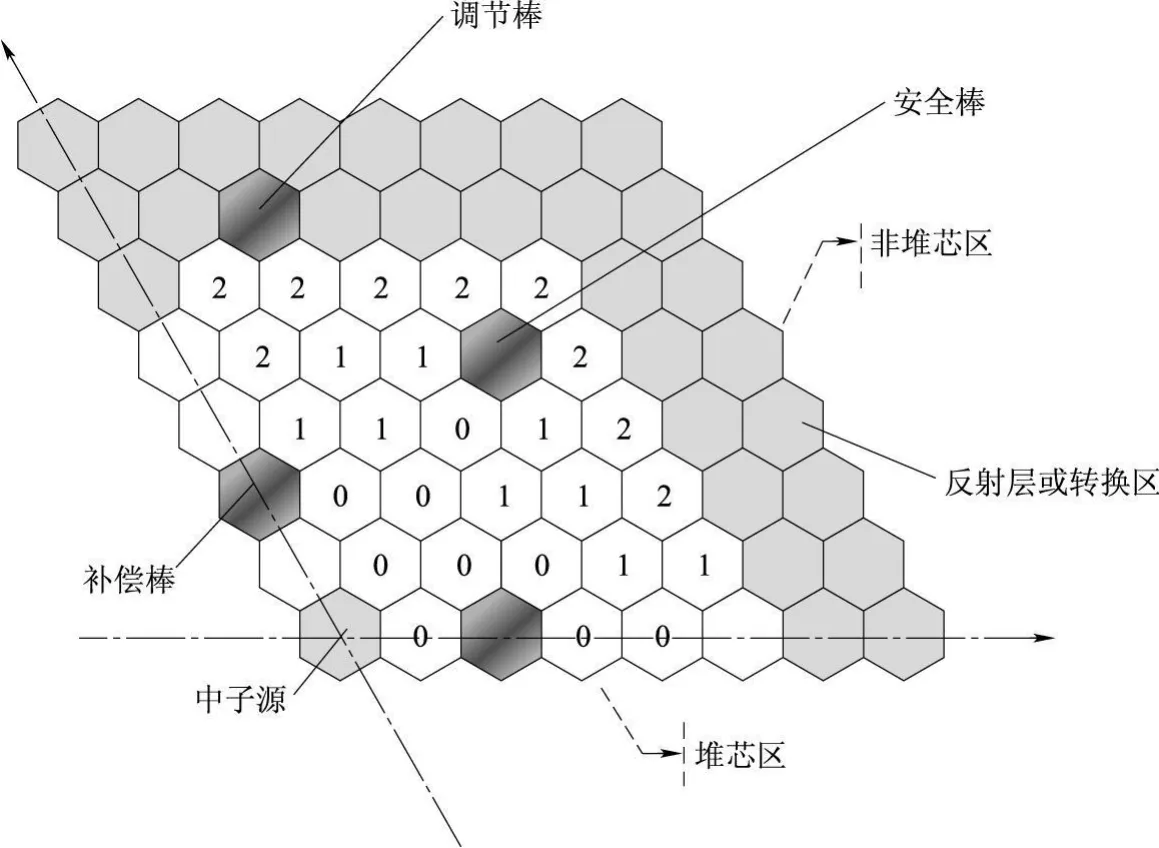
图8 优化末最优方案图Fig.8 Optim ized loading pattern

将图8中第4排的新燃料组件与第3排的经历过1个循环的组件相互换,进行全堆迭代计算后可知循环长度会变长但是幅度很小,相应的卸料燃耗会加深但是幅度也很小,燃料棒最大线功率的变化也非常小。这说明,在所给的限制条件下,经过2 000个方案的优化计算,最终的优化方案已经进入了最优化区域。

3 结论

研究显示,平衡循环倒料换料的优越性,进行倒料可以在不突破限值的情况下尽可能的加大平均卸料燃耗;表1以及图7和图8都说明,优化所得到的最优方案虽然可能不是最优方案但已经进入了最优化的区域,这说明CSA算法可以成功地用于小型快堆的平衡循环倒料优化,这为快堆燃料管理程序的开发奠定了一个基础。

[1] 刘志宏.压水堆多循环燃料管理优化研究[D].清华大学,2003.