基于GRNN的输电线路覆冰厚度预测方法研究

蓝道林 郑振华

（1．衢州电力局，衢州 浙江 324000；2.太原理工大学，太原 030024）

1 引言

随着国民经济的发展，社会对电力供应的安全与稳定的要求越来越高，但是输电线路覆冰成为了影响电力安全供应的重大因素。输电线覆冰带来的后果是可能引起跳闸，带来电力事故。

表1罗列了最近几年我国输电线路覆冰的灾害情况。

表1 输电线路覆冰灾害情况表

由此可见，研究输电线覆冰对于提高电网运行的安全性，电网建设的可持续发展具有非常重要的意义。

输电线路覆冰受众多因素的影响，各影响因素与覆冰厚度之间存在着高度的复杂性和非线性。据有关报告所言，现有的导线覆冰物理模型有十几种，但按权威部门的说法，没有一个模型通过了与实际覆冰数据的比较而得到完全的验证，而人工神经网络是人工智能中一个最活跃的分支，又是一个非线性动力系统，在解决这类预测问题上具有明显的优势。本文引入人工神经网络（ANN）,重点介绍基于GRNN的输电线路覆冰厚度的预测模型。

2 BP神经网络及其主要的缺陷

2.1 BP算法的学习过程

（1）网络的初始化：输入学习率η，动量因子α；给定最大学习误差ε（收敛精度）；给各边连接权wij和神经元阈值θj为小的随机值。

（2）为网络提供学习样本，即输入向量{xi-1,xi-2,…,xi-p}和输出向量{yi}。

（3）计算网络的实际输出。

计算网络的输出值

（4）计算网络误差E

（5）判断：如果E＜ε，学习结束，否则转入（3）。

2.2 BP神经网络建模的主要缺陷

标准 BP算法具有简单易行、计算量小、并行性强等优点，是目前神经网络训练采用最多也是最为成熟的训练算法之一。它的实质是求解误差函数的最小值问题，由于它采用非线性规划中的最速下降方法，按误差函数的负梯度方向修改权值，因此通常存在学习收敛速度太慢,不能保证收敛到全局最小点等缺点。

3 广义回归神经网络

广义神经网络 GRNN是DonaldF.Specht提出的，是Rbf神经网络的一个分支，一种基于非线性回归理论的前馈式神经网络模型。该网络在逼近能力和学习速度上有较强的优势，预测效果好。

GRNN神经网络结构一般分为3层，输入层，径向基隐层，线性输出层，其网络结构与径向基网络接近，仅在输出的线性层有一些不同。其网络结构如图1所示，径向基隐层包含的单元个数等于训练样本数，R表示网络输入的维数，Q表示每层网络中的神经元个数即训练样本数，b1为隐层阈值，设置为0.834/C，可通过改变C的值来调节它。线性输出层的权值函数为规范化点积权函数，它将隐层的输出与本层的权值w的点积作为权输入，直接送入传递函数，即 nprod环节利用函数normprod计算出网络的输出向量n2,它的每一个元素就是向量a1与权值矩阵lw2.1每行元素的点积再除以向量a1各元素之和，并将结果n2提供给线性传递函数a2=purelin(n2)，计算网络输出。

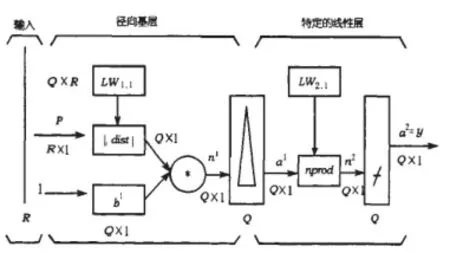
图1 GRNN网络结构图

GRNN神经网络的理论基础是非线性回归分析。设随机变量x和y的联合概率密度函数为f(x,y),已知x的观测值为X，则y相对于X的回归，即条件为：

如果GRNN神经网络的概率密度函数采用高斯函数，则网络的输出为：

4 BP神经网络预测模型和GRNN神经网络预测模型仿真比较

4.1 数据采集和预处理

神经网络智能辨识模型的建立需要大量数据进行训练，所以选择一个典型的覆冰产生地极其重要。本论文的数据采集通过导线覆冰在线监测系统获得,此系统建立在忻州供电局神原 I回线路上，装设在109杆塔处。109杆塔处在高山分水岭型地形的背风坡处，线路翻越分水岭，空旷开阔，容易出现强风及严重覆冰情况，尤其在山顶及迎风坡侧，含有过冷却水滴的气团在风力作用下，沿山坡强制上升而绝热膨胀，使过冷却水滴含量增大，导致导线覆冰增加。109杆塔所处分水岭微地形如图2所示。

图2 分水岭微地形示意图

训练模型所用的样本来自于现场所采集的数据，采集到398组数据样本，从中选取388组数据对神经网络进行训练，另10组数据作为测试样本，其中每组数据包括三个输入元素，分别为温度、湿度、雨量，一个目标元素，即输电线路覆冰厚度。由于网络训练前的数据可影响网络的学习速度、机构复杂性和预测精度，通常数据在[-1,1]之间时，数据梯度变化明显，收敛速度快，因此利用Matlab仿真软件先对输入输出数据进行归一化处理，将数据映射到[-1，1]之间，这样便于提高神经网络的训练速度。

4.2 BP网络模型的建立以及预测结果

本BP神经网络模型包括四层：输入层、两个隐含层及输出层，其中输入层有三个节点，隐含层的节点数不确定，需要在训练过程中进行调整；输出层包含1个节点，表示覆冰的厚度。采用训练速度最快的Levenberg-Marguardt规则训练前向网络。显示频率disp_freq=10；最大训练次数max_epoch=2000；误差目标 err_goal=0.001；学习速率lr=0.05。论文中的程序都是用Matlab进行编程。

用训练好的神经网络模型进行 Matlab仿真测试，计算可得合理隐含层节点数喂[312]之间的整数，经过试验可知隐含节点数为11时误差最小，拟合情况最为理想，图 3给出 BP网络模型对覆冰厚度的仿真结果。

图3 BP模型预测结果

其中，图中的“+”为实际值，“o”为预测值。

4.3 GRNN模型的建立以及预测结果

GRNN网络模型的建立，主要包括输入层，输出层因子的选取，径向基函数分布密度spread的确定。

其中，输入层有三个节点，输电线覆冰厚度值为输出因子。经过反复试验，本文将分布密度spread确定为0.13。

在Matalb神经网络工具箱中，GRNN网络可以直接利用newgrnn函数调用。格式为：net=newgrnn(p,t,spread)

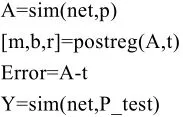
其中 net=newgrnn用于在对话框中建立一个GRNN网络；p是训练样本；t为训练样本目标值；spread为径向基函数的分布密度，它可以对grnn网络的性能产生重要影响。通常spread越小，网络的逼近效果越好，因此，在网络设计过程中可调整spread的值，知道达到比较理想的预测精度为止。

图4给出了GRNN网络模型对覆冰厚度的仿真结果。

图4 GRNN模型预测结果

其中，图中的“+”为实际值，“o”为预测值。

4.4 仿真结果比较

表2和表3分别给出了BP网络模型和GRNN网络模型预测结果对比以及BP网络模型和GRNN网络模型预测效果对比。

表2 BP网络模型和GRNN网络模型预测结果对比

表3 BP网络模型和GRNN网络模型预测效果对比

根据表3中的数据可知，GRNN网络的预测值更接近实际值，具有更好的逼近效果，同时表3中，GRNN网络模型的平均相对误差为1.2399，小于BP网络模型的2.4854，而且GRNN网络模型的最大相对误差为-2.28，BP网络模型的最大相对误差为-4.995，所以根据表2、表3以及仿真图形可以看出，GRNN模型比BP模型具有更高的预测精度。

同时从表2、表3中可以看出，GRNN模型的训练步数为56步，而BP网络模型的训练步数为893步，所以无论从预测精度还是训练步数上考虑，对于预测输电线路覆冰厚度，GRNN网络模型的预测效果要比 BP神经网络模型的预测效果要好。更适合预测输电线路覆冰厚度的预测。

5 结论

本文通过分析整理忻州输电线路的气象数据（包括湿度、温度、雨量）以及覆冰厚度等历史数据，建立了基于GRNN网络输电线覆冰厚度预测模型，对输电线路未来覆冰量厚度进行了预测，仿真结果表明，相比较BP网络模型，GRNN网络模型训练所需的步数更少，而且能更准确地预测输电线路覆冰厚度。

[1] 蒋兴权.输电线路覆冰机理与防冰新技术研究.中国科学技术协会首届青年学术年会论文集,工科分册（上册）.北京：学技术出版社,1992:110-15.

[2] 靳潘,潘俊波,谭永东,神经网络与神经计算机原理[M].成都：西南交通大学出版社,1991.

[3] Naquesh.D.S.,Datta.G.L. Modeling of fillet welded joint of GMAW process: Integrated approach using DOE, ANN and GA. International Journal on Interactive Design and Manufacturing, v2, n3, p127-136, 2008.

[4] 孙湘海.基于GRNN模型的城市道路短期交通流预测研究[J]. 科学技术与工程,2007(12).

[5] 高雷,曹永锋,李芬香．基于BP神经网络的个体定税预测模型[J]. 统计与决策,2007(4):104-106.

[6] 梁凤国.李帅莹.于淼.马宗正基于 GRNN神经网络的参考作物腾发量预测[J]. 人民长江,2009(5).