曲柄摇杆式脉动无级变速器的机构参数优化

徐彦兰,王玉顺

(1.山西农业大学 工学院,山西太谷 030801,2.山西农业机械化学校,山西 平遥031101)

播种机上配置脉动无级变速器是一项有发展潜力的技术,它结构精巧紧凑,变换传动比便捷并能全面适应各类播种要求,但存在传动比不平稳的本质缺陷,因此,机构参数的优化是非常必要的。

曲柄摇杆式脉动无级变速器是脉动类无级变速器中结构较简单的一种,但也是输出转速不平稳较为严重的一种[1～5],研究它的机构优化问题对此类变速器的设计和制造具有普遍意义。

国内有学者以输出角速度脉动率、角速度波谷处角加速度突变量等的加权和为目标函数,研究了曲柄摇杆与双摇杆串联六杆机构、曲柄摇块式机构等的参数优化问题[6～8],并获得有意义的优化结果。

本文拟以表征输出转速平稳性的变异系数为目标函数,辅助以仿真试验,探讨变速范围内曲柄摇杆式脉动无级变速器的综合优化问题。

1 曲柄摇杆式脉动无级变速机构原理

如图1所示,曲柄摇杆脉动无级变速器主要有曲柄轴A(输入轴)、曲柄 AB、连杆 BC、摇杆 CD、摇杆轴D(输出轴)、超越离合器E、机架AD等组成,其中摇杆CD通过超越离合器单向驱动摇杆轴D。工作时,假定曲柄轴A恒速旋转,曲柄AB通过连杆BC驱动摇杆CD往复摆动。若摇杆CD正向摆动,超越离合器作用会使摇杆轴D产生一定的转角,若摇杆CD反向摆动,超越离合器作用会使摇杆轴D脱离摇杆驱动,无转角产生。基本原理是,将输入轴的匀速转动转变为摇杆的往复摆动,再通过单向超越离合器将摇杆的往复摆动转换为输出轴的单向脉动旋转。

图1 曲柄摇杆式脉动无级变速器结构Fig.1 The structural of impulse steeples speed variation

改变曲柄半径则会变换摇杆摆角的大小,从而实现传动比的无级调节。只用一组曲柄摇杆机构驱动摇杆轴称作单相结构,用二组曲柄摇杆机构同时驱动摇杆轴称作二相结构,依此类推。采用多相结构可以获得脉动幅度更小的输出转速,相互间隔一定相位差的多组曲柄摇杆机构共同驱动一个摇杆轴,但只有正向摆动转速最快的那个摇杆起作用,其余摇杆处于脱离驱动状态。

2 机构参数的优化设计

机构参数指各个构件的长度,优化设计的目的就是确定输出转速脉动达最小的机构参数,以改善摇杆轴输出转速的平稳性。

2.1 机构矢量分析

如图2所示,机架AD置为水平,以A为原点建立直角坐标系,水平向右为 轴正向,垂直向上为轴正向。机构的各个构件分别用矢量表示,转角自轴正向起始度量,逆时针为正,顺时针为负。

图2 无级变速机构闭环矢量图Fig.2 Closed loop vector diagram of steeples variablemechanism

曲柄AB表为矢量r1,其矢模r1和矢角 θ1;连杆BC表为矢量r2,其矢模 r2和矢角θ2;摇杆CD表为矢量r3,其矢模 r3和矢角θ3;机架 AD表为矢量r4,其矢模r4和矢角θ4=0。改变曲柄长度r1可实现传动比的无级调节。机构的4个位移矢量之间存在下面的关系:

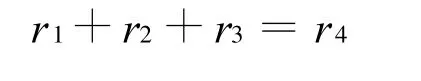
矢量分解为水平分量和垂直分量,则上面的矢量方程可表为矩阵形式:

分别作如下定义,相对曲柄长度R1=r1/r3,相对连杆长度R2=r2/r3,相对摇杆长度R3=r3/r3=1,相对机架长度R4=r4/r3,则得构件相对长度表示的位移矩阵方程:

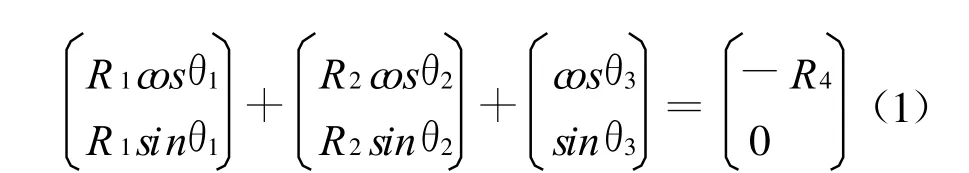
2.2 机构优化模型

优化模型讨论设计变量、目标函数和约束条件三个问题。

2.2.1 设计变量

摇杆轴的转速特性实质上决定于r1、r2、r3和等r4个机构参数的比例关系,因此优化问题的设计变量确定为R1、R2和R4,表为向量 x如下:

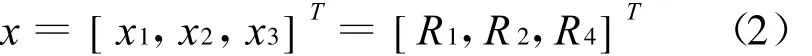
2.2.2 目标函数

目标函数以实现摇杆轴转速脉动最小为出发点建立。考察一个工作周期,参见图2,曲柄自极限位置BS恒速转动到极限位置BZ,亦即曲柄从起始角θ1S旋转到终止角θ1Z;同时摇杆自极限位置CS摆动到极限位置CZ,亦即摇杆从起始角θ3S旋转到终止角θ3Z,此过程为机构的驱动行程,剩余行程为机构的回程。参见图2中的 Δ ACSD,由余弦定理可知:

解得驱动行程的摇杆起始角θ3S如下:

θ3S表为设计变量的函数:

同理,分别得驱动行程的摇杆终止角θ3Z、曲柄起始角θ1S和曲柄终止角θ1Z如下:

定义无级变速器平均传动比iP为摇杆轴平均转速与曲柄轴平均转速之比,则由式(3)和式(4)可得:

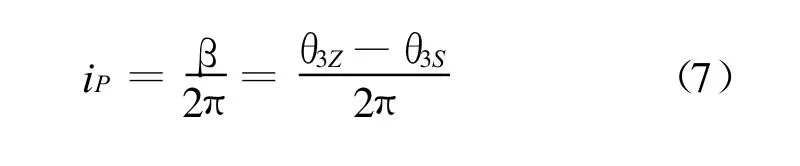
由式(1)可推得:

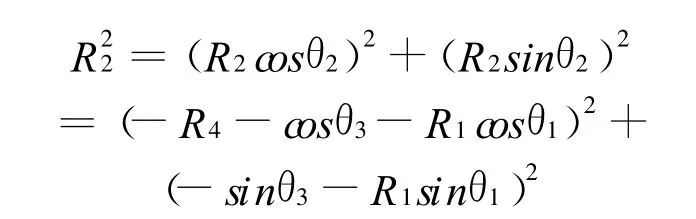
借此构造设计变量x的一个函数φ(x)如下:

考察驱动行程,曲柄转角θ1自θ1S至θ1Z等间隔取n个值,对于每一个 θ1值,用优化方法使φ(x)的绝对值｜φ(x)｜达最小,从而解出与每个θ1值对应的 θ3值,获得摇杆转角 θ3自 θ3S至θ3Z的n 个值 。θ3的n个值表为向量θ3,其中第一个取值θ3[1]=θ3S,最后一个取值 θ3[n]=θ3Z,即

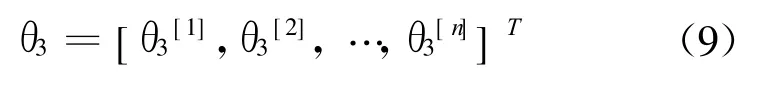
由式(9)得摇杆转角的增量序列,即如下向量:

对摇杆转角的增量序列 Δ θ3求取均值m(Δ θ3)和标准差 s(Δ θ3)[9],目标函数拟采用摇杆转角增量序列的变异系数,即:

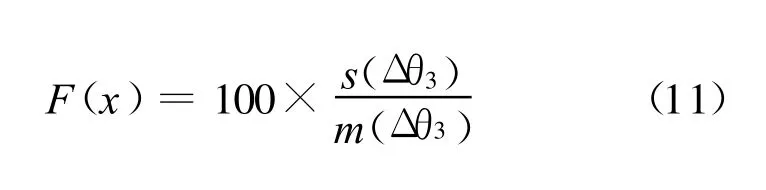
转角增量序列的变异系数实质上是转速的变异系数,反映摇杆轴转速的相对脉动程度,其值愈小摇杆轴转速愈平稳,适宜做目标函数。

2.2.3 约束条件

考虑机构运动的合理构件长度、曲柄长度调节和制造尺寸不必过大,选择下述约束:

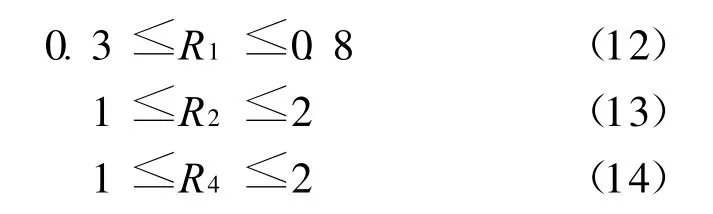
考虑机构运动曲柄存在的条件,则有约束:

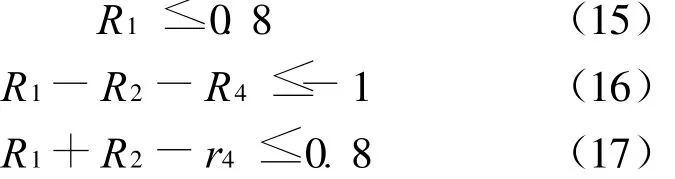
为保证曲柄摇杆机构的顺利传动,传动角的值应在允许范围,等价地换算成连杆与摇杆的夹角φ,则其取值范围确定为φ∈(30°,150°)。参见图2,由余弦定理可知

确定与构件起始夹角φS有关的约束如下

同理,确定与构件终了夹角有关的约束如下

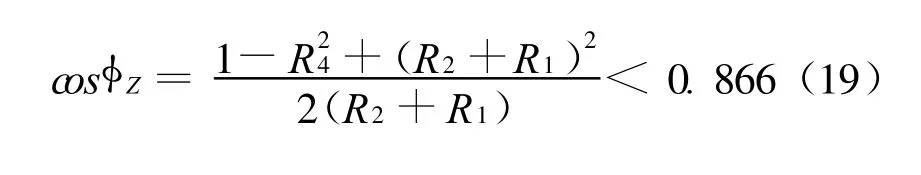
研究曲柄摇杆式脉动无级变速机构发现,机构平均传动比iP的值不同,机构参数的优化结果亦不同,即iP的每个值都对应一组优化的机构参数。因此,考虑传动比的合理范围,平均传动比可分别取值构成等式约束,如下所示:

2.2.4 优化问题概述

综上所述,目标函数F(x)由式(3)至式(11)的一组公式计算,优化模型可归结为

优化的目标,是要获得使摇杆轴转速脉动达最小的机构参数,以改善转速输出的平稳性。

2.3 优化结果及讨论

采用MATLAB/OptimizationToolboxTM/fmincon函数编程,求解式(21)描述的优化模型,结果汇总于表1并展示于图3。

表1 机构参数的优化结果Table 1 The optimization results of mechanism parameters

图3 平均传动比对机构参数优化的影响Fig.3 The effect of the average transmission ratio on the optimization of mechanism parameters

从表1数据和图3可看出,就优化的机构参数而言,当平均传动比iP增大时,曲柄长度R1近乎直线增大,连杆长度R2微幅增大再减小,而机架R4较大幅减小,目标函数F(x)的值一直减小。优化结果说明,传动比较大时,较大的曲柄长度配套较小的机架长度,才能获得较平稳的摇杆轴转速。

无级变速器的所有机构参数均可调节是不现实的,最终采用的优化机构参数,实质上是确定曲柄长度的调节范围,而连杆长度R1和机架长度R2可从表1中选一组数据,这一问题后面将讨论。

3 机构转速的仿真试验及分析

仿真试验主要解决三个问题:(1)验证优化结果的正确性;(2)探讨摇杆轴转速特性与机构相数的关系;(3)确定最终的优化机构参数。

3.1 机构速度矩阵方程

式(1)所示的位移矩阵方程对时间求一阶导数,得机构速度矩阵方程如下:

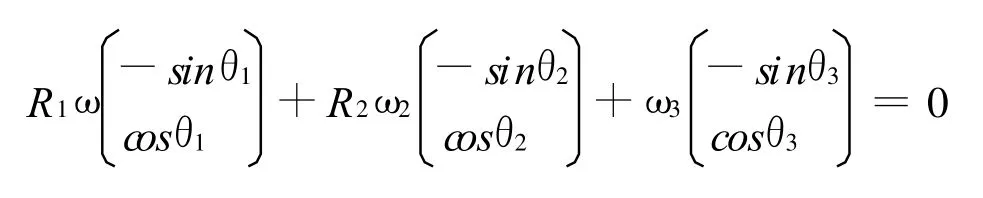
机构速度矩阵方程变换为下面的形式:

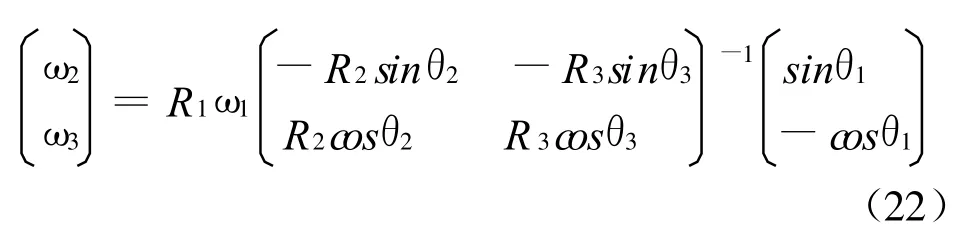
式中 ω1、ω2和 ω3分别是角位移 θ1、θ2和 θ3对时间的一阶导数,即曲柄转速、连杆转速和摇杆转速,逆时针旋转为正,顺时针旋转为负。

3.2 仿真试验的误差方程

由式(1)构造位移仿真误差方程:

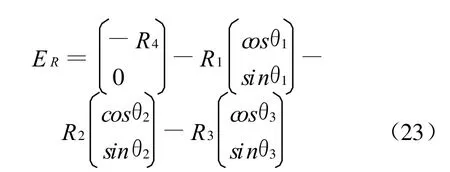
理论上ER≡0,但仿真不可避免地存在误差,从而使ER≠0,式(23)用于检验位移仿真结果的精确性。

由式(22)构造转速仿真误差方程:

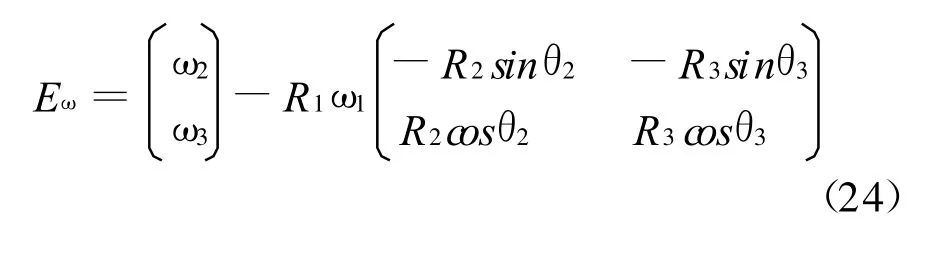
理论上Eω≡0,但仿真不可避免地存在误差,从而使Eω≠0,式(24)用于检验转速仿真结果的精确性。

3.3 机构转速与位移的仿真模型

利用MATLAB建立单相结构曲柄摇杆机构的SIMULINK仿真模型[10],详见图4。该仿真模型主要由三个积分模块和两个调用自定义函数的模块组成,自定义函数mdcompvel.m根据式(22)编程,自定义函数mderrorcheck.m根据式(23)和式(24)编程。SIMULINK 仿真模型输出 ω1、ω2、ω3、θ1、θ2、θ3、ER、Eω及时间t等9个变量的仿真结果。

图4 机构转速与位移的SIM ULINK仿真模型Fig.4 The SIMU LINK simulation model of the rotational speed and displacement for crank-rocker mechanism

3.4 仿真试验方案

由于不同传动比机构参数的优化结果不同,故挑选二套优化的机构参数做仿真试验。因曲柄转速对所研究问题无影响,故试验选用7 r◦s-1。

表2方案的试验对象机构Ⅰ对应iP=1/6(传动比中值)的优化结果,即相对曲柄长度R1的调节范围是0.304～0.849,相对连杆长度 R2为1.419,相对机架长度R4为1.591。表中驱动行程的曲柄起始角θ1S、连杆起始角θ2S和摇杆起始角θ3S用于设置图4所示仿真模型的积分模块,单位均为弧度。

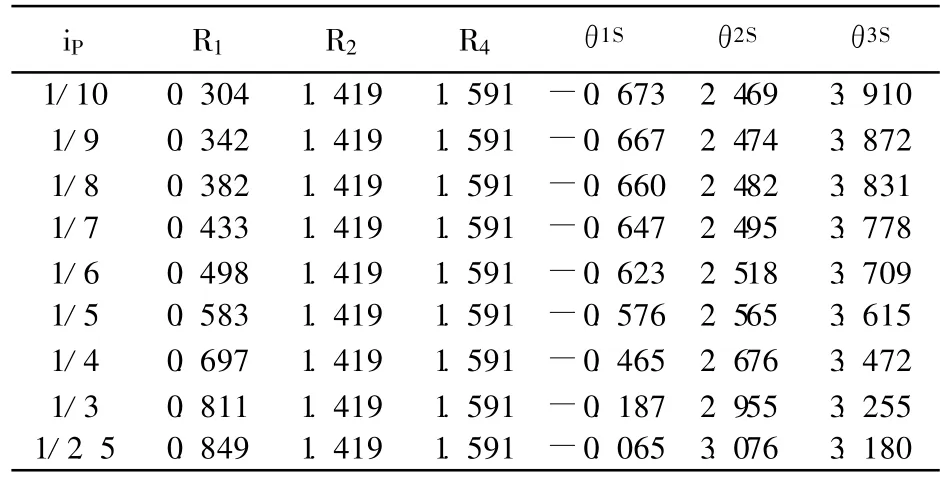
表2 机构Ⅰ的试验方案Table 2 The test scheme of mechanismⅠ

表3方案的试验对象机构Ⅱ对应iP=1/3(传动比较大值)的优化结果。即相对曲柄长度R1的调节范围是 0.304～0.849,相对连杆长度R2为1.342,相对机架长度 R4为1.348。

表3 机构Ⅱ的试验方案Table 3 The test scheme of mechanismⅡ

3.5 仿真结果及分析

运行图4所示的SIMULINK仿真模型,按表2和表3的要求分别做仿真试验,并根据各种使用目的对仿真输出数据进行再处理,由处理结果作如下讨论。

3.5.1 摇杆轴转速特性

图5展示机构Ⅱ的摇杆转速特性。由于相对曲柄长度较大,转速曲线的正弦性较差,正峰值绝对值较小,负峰值绝对值较大,机构有较强的急回作用。

图6展示机构Ⅱ单相结构的摇杆轴转速特性。从图中可看出,超越离合器作用使摇杆轴转速只取图5所示摇杆转速的正值部分,故单相结构不能连续驱动。

图7展示机构Ⅱ三相结构的摇杆轴转速特性。从图中可看出,超越离合器作用使摇杆轴转速等于较大的那个摇杆转速,三相结构能够连续驱动,但存在转速脉动。研究表明,实际上二相结构就实现了连续驱动,只不过转速脉动更大罢了。

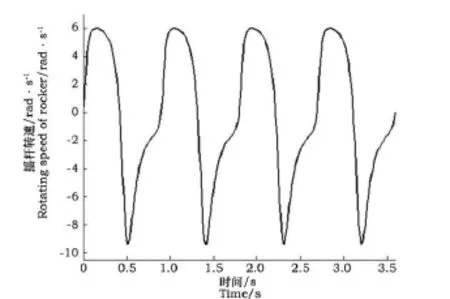
图5 摇杆转速的时变曲线Fig.5 The change curve of the time varying for rocker

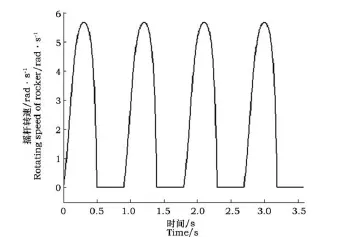
图6 单相结构摇杆轴转速的时变曲线Fig.6 The change curve of the time varying for the single-phase structure of rocker

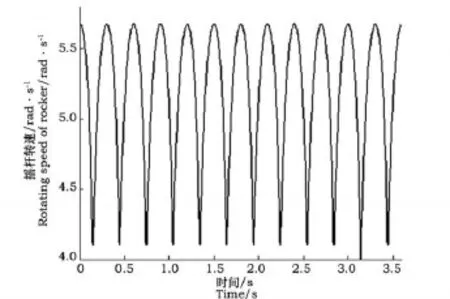
图7 三相结构摇杆轴转速的时变曲线Fig.7 The change curve of the time varying for the three-phase structure of rocker

3.5.2 平均传动比特性

图8至图11的图例中的1、2、3、4和5分别指单相、二相、三相、四相和五相结构。

图8 机构Ⅰ的平均传动比特性Fig.8 The characteristics of the average transmissionratio for mechanismⅠ

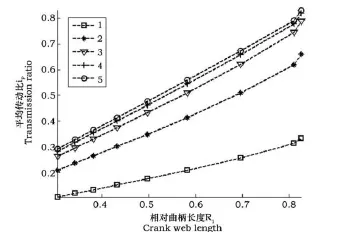
图9 机构Ⅱ的平均传动比特性Fig.9 The characteristics of the average transmissionratio for mechanismⅡ

从图8和图9可看出,平均传动比与相对曲柄长度的关系近乎直线,尤其机构Ⅱ的直线性更强。平均传动比随着相数的增多而增大,但三相、四相和五相结构的传动比值较接近。综合考虑可线性调节传动比和简化变速器结构,机构Ⅱ的三相结构较有优势。

3.5.3 摇杆轴转速特性的多相结构比较

从图10和图11可看出,相数越多摇杆轴转速变异系数越小,但三相、四相和五相结构的变异系数较接近。当相对曲柄长度增大时,机构Ⅰ单相和二相结构的摇杆轴转速变异系数小幅增大,而三相、四相和五相结构却减小,机构Ⅱ的变异系数均减小。综合考虑转速平稳性和简化变速器结构,机构Ⅱ的三相结构较有优势,这与传动比特性的研究结论一致。

图10 机构Ⅰ的摇杆轴转速平稳性Fig.10 The speed stationarity of the rocker for mechanismⅠ

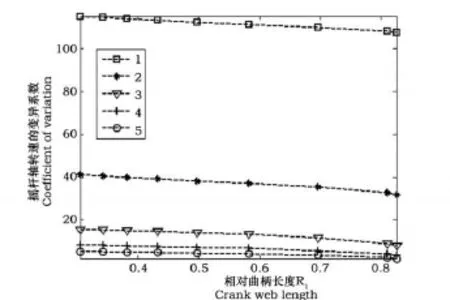
图11 机构Ⅱ的摇杆轴转速平稳性Fig.11 The speed stationarity of the rocker for mechanismⅡ

3.5.4 位移和转速的仿真误差

由式(23)和式(24)定义仿真误差,在曲柄调节的整个范围内,机构Ⅰ的位移仿真误差达0.0756×10-6～2.83×10-6,机构Ⅱ的达 2.00×10-6～4.18×10-6;机构Ⅰ的转速仿真误差达1.16×10-16～4.4910-16,机构 Ⅱ的达 1.2310-16～5.5710-16,其变化趋势详见图12和图13。微小仿真误差表明,仿真试验结果可靠、可用。

4 结论与讨论

图12 机构Ⅰ与机构Ⅱ的位移仿真误差Fig.12 The displacement simulation error for mechanismⅠandⅡ

图13 机构Ⅰ与机构Ⅱ的转速仿真误差Fig.13 The rotate speed simulation error for mechanismⅠandⅡ

优化结果表明,每个可行的平均传动比均对应一组优化的机构参数,随平均传动比ip增大曲柄长度R1近乎直线增大,连杆长度R2微幅增大再减小,机架R4较大幅减小。传动比较大时,较大曲柄长度配套较小机架长度才能获得较平稳的摇杆轴转速。

仿真试验表明,平均传动比与相对曲柄长度的关系近乎直线,尤其机构Ⅱ具有更强的直线性;虽然平均传动比随相数增多而增大,但三相、四相及五相结构的传动比值较接近。综合考虑简化结构和便捷调节传动比,机构Ⅱ的三相结构较有优势。

仿真试验表明,相数愈多及相对曲柄长度愈大,则三相、四相及五相结构的摇杆轴转速变异系数愈小,但它们的变异系数值较接近。综合考虑转速平稳性和简化变速器结构,机构Ⅱ的三相结构较有优势,这与传动比特性的研究结论一致。详见图10和图 11。

在整个曲柄调节范围内,机构Ⅱ的位移仿真误差达2.00×10-6～4.18×10-6,转速仿真误差达1.2310-16～5.5710-16。微小仿真误差表明,仿真试验的结果可靠、可用。

综上所述,综合考虑输出转速平稳性和简化变速器结构,无级变速器宜采用三相结构,以调节曲柄长度的方式调节传动比,其余构件长度不变。一组较优的机构参数是,相对曲柄长度R1在0.304～0.849范围内调节,相对连杆长度R2取1.342,相对机架长度R4取1.348。优化机构的摇杆轴转速变异系数在7.766至15.567之间,且曲柄长度愈大变异系数愈小。

[1]阮忠唐.机械无级变速器设计与选用指南[M].北京:化学工业出版社,1999:1-75.

[2]Thomas GF,Greenwood CJ.T he design and development of an experimental traction drive CV T for a 2.0-liter FWD passenger car[J].SAE Paper,1991(910408):535-544.

[3]阮忠唐.机械式无级变速器[M].北京:机械工业出版社,1983:36-89.

[4]梁海顺.摇块式无级变速器的工作原理和运动性能分析[J].机械,1995(1):120-124.

[5]廖林清.Power-Matic机械无级变速器的结构及运动学研究[J].机械设计,2002(6),23-24.

[6]王蕊.脉动式无级变速器的优化设计与仿真[D].吉林大学,2005.

[7]刘伟,赵健.脉动无级变速器型及尺度优化综合设计[J].机械,1996(3):44-49.

[8]宋东.Zero-Max型无级变速器特性研究和参数优化[D].湘潭大学,2007.

[9]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2001(3):65-77.

[10]周进雄.机构动态仿真(使用MAT LAB和SIM ULINK)[M].西安:西安交通大学出版社,2002:101-112.