对几种不同维数据融合方法的仿真对比研究

朱 捷，朱宏伟，何 伟

（1.炮兵指挥学院廊坊校区，河北 廊坊 065000；2.防空兵指挥学院，河南 郑州 540052）

由于装备体制不同，当前对空情报雷达网数据处理中存在对目标位置的量测数据维数不匹配的问题。其典型情况是，两坐标雷达和三坐标雷达同时对目标进行观测所获得的观测信息中，三坐标雷达比两坐标雷达多获得目标的高低角坐标信息。

为了能准确地对维数不匹配的观测信息进行融合，文献[1-3]中讨论了通过建立状态之间的映射关系，对不同维目标估计状态进行融合的映射法；文献[4]提出将三坐标雷达的高低角信息赋予两坐标雷达后进行位置融合并得到系统航迹的升维法；文献[5]则提出将三坐标雷达的量测分解后分别进行相关和融合处理的分维法。

本文通过计算机仿真技术，模拟了映射法、升维法、分维法对不同维量测数据的融合过程，并对其融合效果进行了对比。

1 算法流程

1.1 映射法融合流程

当融合系统采用映射法处理维数不匹配观测信息时，首先给两坐标雷达的量测加入目标的虚拟高度，而后再经过滤波、坐标转换、时间对准等数据处理过程，在统一的直角坐标系下完成点迹关联和航迹融合，最终形成系统航迹。其融合流程如图1所示。映射法融合框架简单、计算简便，且能得到三坐标系统航迹。但由于加入了虚拟的高度值，降低了关联概率并存在较大的系统动态误差。

图1 映射法融合流程图

1.2 升维法融合流程

升维法在获得相关结果后，将三坐标雷达的俯仰信息经转换赋给两坐标雷达，而后再对网内雷达的数据进行处理。升维法避免了系统动态误差的产生，但融合数据处理过程中计算量比较大。

当系统采用升维处理时，整个处理过程如下：

1）将三坐标雷达量测的俯仰信息从状态矩阵中删除，在与两坐标雷达获得的目标状态矢量经数据预处理后，进行相关处理，获得航迹的相关信息；

2）将三坐标雷达测量点迹的俯仰测量信息赋给两坐标雷达，经坐标转换后得出相对两坐标雷达站的俯仰测量信息；

3）通过坐标转换将各雷达站对目标的量测统一在同一直角坐标系下，并进行航迹融合得出系统航迹。升维法融合流程框架如图2所示。

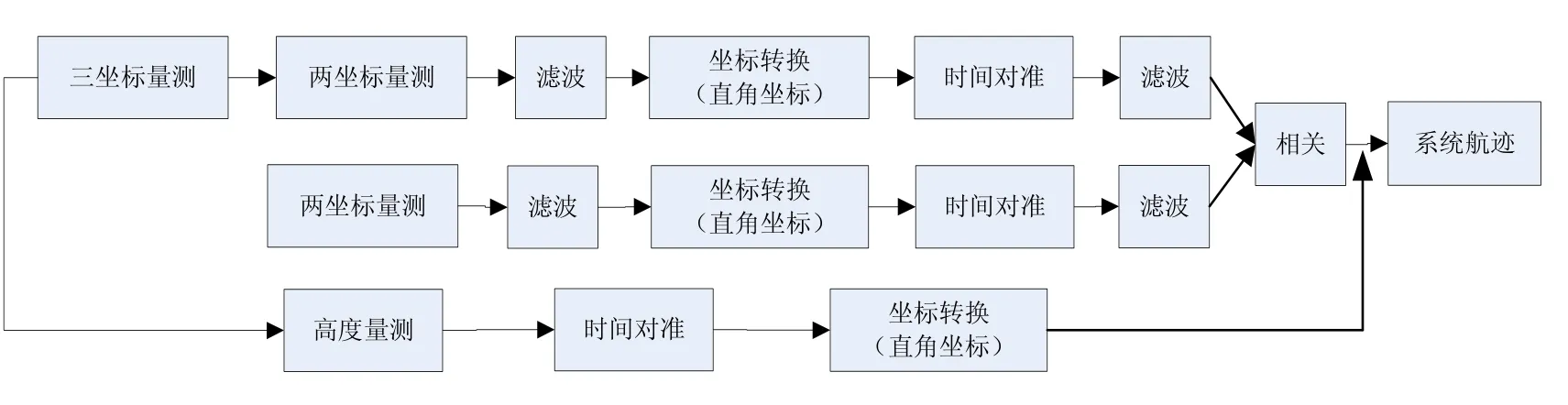
图2 升维法融合流程图

1.3 分维法融合流程

分维融合方法借鉴天文中常用的天球坐标系，在数据关联和航迹合成阶段引入了天球坐标加地心距离的目标位置表示方法，在数据关联和航迹融合的过程中分别对天球坐标与地心距离进行处理，简化了对不同维观测数据的处理过程。

当系统采用升维法处理时，整个处理过程如下：

1）将雷达测定的目标信息送至融合中心后，假设两坐标雷达测得目标高度为0，同时由三坐标雷达的量测生成对应的地心距离，并进行时间对准等数据预处理；

2）将各雷达的目标本地坐标转换为大地直角坐标并进行滤波处理；

3）在天球坐标系内进行目标关联。若量测被关联，则对地心距离和两雷达量测进行融合，得到融合航迹点坐标，并加入所关联的天球坐标系系统航迹。

分维法融合流程框架如图3所示。

图3 分维法融合流程图

2 目标跟踪及关联算法

为了验证三种融合方法的有效性和融合效果，本文在三种融合方法的跟踪和关联过程中分别采用了经典的自适应α-β滤波算法和修正的K近邻关联算法对目标进行跟踪和关联。

2.1 自适应α-β滤波算法

在自适应α-β滤波算法中，状态估计的一步预测方程为

一步预测误差方程为

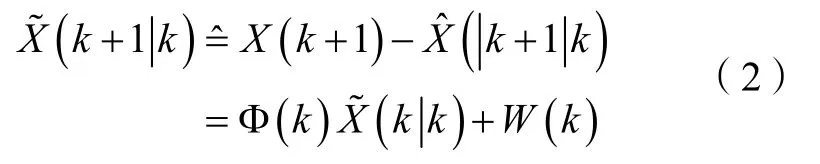
其一步预测协方差为

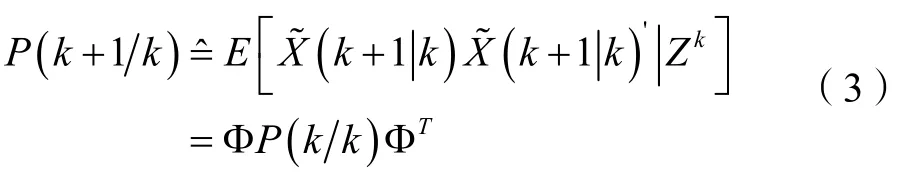
类似地，预测的观测向量为

状态滤波估值为

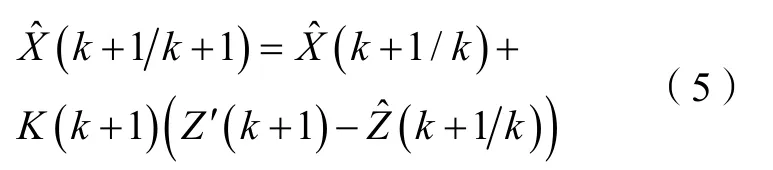
其中，增益矩阵K(k+1)为

估值误差协方差矩阵为

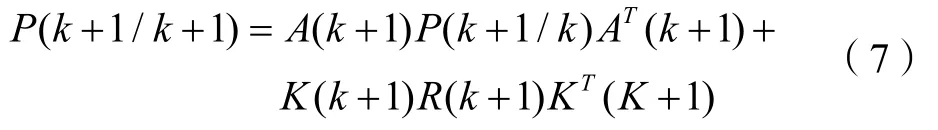
式中，

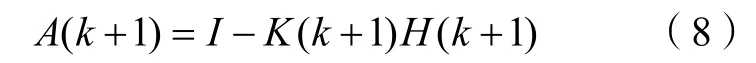
定义r为目标的机动指数，其计算公式为

显然，r值的大小可以反映目标的激动程度。如果把反映目标机动的值看作信号，也可以将r值称作信噪比。

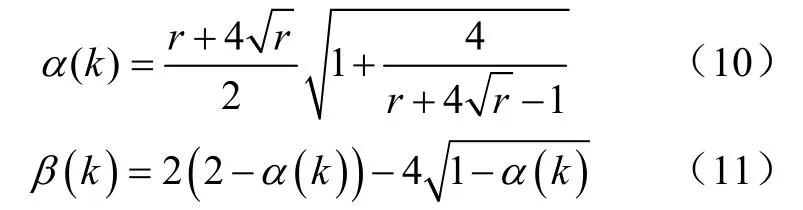
此时，若定义残差为

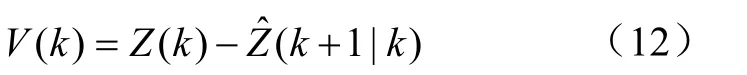
则 V(k)不仅反映了观测误差的大小，也反映了目标机动的情况。设残差有N个采样值，则可得到目标机动加速度方差的表达式

式中，N为雷达天线扫描周期的滑窗。

这里N一般选3-5。将作为带入式（14），即可得到自适应滤波系数α(k)和β(k)。

2.2 修正的K近邻关联算法

修正的K近邻法关联准则为：取两个正整数N0和K，其中N0≥ 2 ，[N0/2]≤K≤N0是关联检验次数。那么，如果在N0次关联检验中有K次满足条件：则两航迹相关。其中，l=1,2…N0，i∈U1,j∈U2。

修正的K近邻算法是一种典型的时空信息融合方案，它将当前检验和历史检验联系起来，把整个检验过程分为关联期、检查期和保持期三个关联阶段。

当进入融合传感器的航迹点数在0N以内时，算法处于关联期。在关联过程中，如果从关联开始到t时刻航迹i和j被判为不关联的次数大于N0−k，则航迹i与j为脱离航迹，无需再进行关联；当关联次数l=N0时（关联期结束），大部分试验系统航迹将转变为确认系统航迹，一部分试验系统航迹由于脱离质量的增加将被撤销。

当关联次数l＞N0时，航迹关联进入检查期。进入关联期后，对于l=N0+ 1 ,N0+ 2 ,N0+ 3连续进行三次x2检验，如果ϖij(k)≤δ，则Tij(k) =Tij(k− 1 ) +1。否则，这里δ是检验门限，根据x2分布的自由度和显著性水平a确定。连续三次检验后，如果Tij(k=N0+3)=3，则i与j成为固定关联对，并进入保持期;若Tij(k=N0+ 3 ) ≤−1，则撤销所对应的系统航迹，并使两个局部航迹重新进入关联期;如果Tij(k=N0+ 3 )=1 ,则再进行两次检验，然后根据Tij(k=N0+ 5 )的取值作最终的判决[6]。

关联检验一旦进入了保持期，其关联对和关联映射赋值便完全确定了，从此不再进行假设检验。

3 仿真实验及结果分析

为了比较三种融合方法对不同维数据的融合效果，分别对两型四部雷达对水平直行航迹和水平急转航迹的数据进行融合仿真试验。

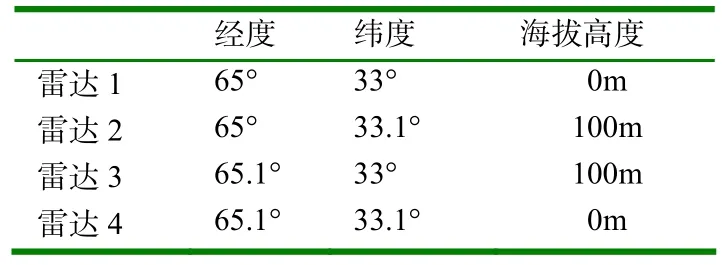
表1 分别设雷达站坐标位置如下

其中，雷达1和3为扫描周期10s，距离精度0.1km、方位精度0.5°、高低角精度0.25°的三坐标雷达；雷达2和4为扫描周期15s，距离精度0.5km、方位精度0.5°的两坐标雷达。

目标航迹分别为：

航线1：目标从东经65◦、北纬30.625◦在7km高度以600m/s的速度向东经66.71◦、北纬34.7◦作水平飞行。

航线2：目标从东经70.72◦、北纬31◦在7km高度以600m/s的速度向东经70◦、北纬33◦水平飞行到达目标点后以10g的加速度右转90◦，向东经72.55◦、北纬32.83◦作水平飞行。

对两种航迹的目标在融合中心分别采用映射法、升维法和分维法对雷达量测进行融合，用计算机分别进行50次模拟。

图4和图5为不同融合方法误差对比图。可以看出，无论是对水平匀速航迹还是急转机动航迹，分维融合方法精度明显高于映射法，而与升维法相当，能够达到较好的融合效果。

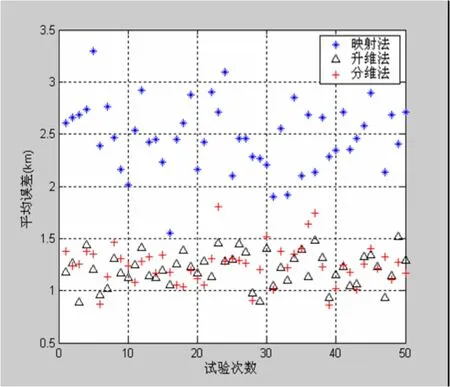
图4 水平匀速航迹融合误差对比图

图5 急转航迹融合误差对比图

表2所示为不同融合方法航迹关联概率及数据处理时间统计结果。可以看出，在平均关联概率方面，三种方法对于水平匀速目标都有较好的关联概率，但对于空中高机动目标，升维法与映射法的关联概率都出现了明显的下降。而分维法对高机动目标仍能保持较高的关联概率，获得更好的关联结果。在数据处理时间方面，分维法对两种典型航迹的数据处理时间比映射法长，而比升维法要短。也就是说分维融合方法对数据的处理量比映射法大，但与精度相似的升维法相比则大大降低了计算量。

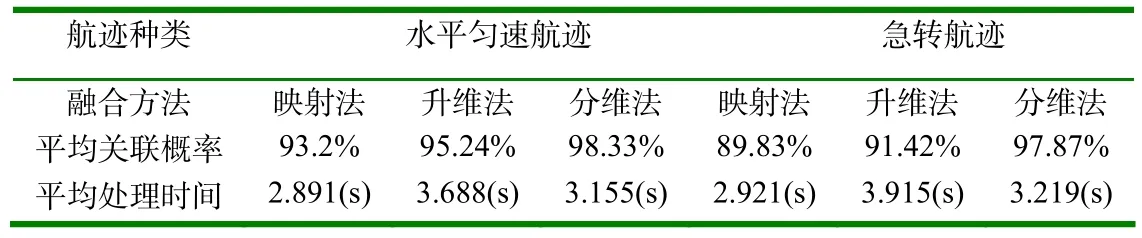
表2 不同融合方法航迹关联概率及数据处理时间统计结果

4 结束语

本文对三种处理不同维数据的融合方法框架和算法特点进行了分析，利用仿真技术对两种典型航迹模拟了三种融合方法的处理过程和融合结果，并对比分析了仿真结果。可以看出，分维法在较小计算量的基础上可以获得较高的关联概率和融合精度，特别是对机动目标的跟踪关联概率明显高于对比的映射法和升维法，相比传统的处理不同维数据的融合方法有较大的改进，更适合跟踪机动目标。本文研究成果对于提高多雷达系统组网中的数据融合处理，具有一定的应用价值和参考意义。

[1]徐毓,李锋.不同维状态的多传感器航迹融合[J].传感技术学报,2004,2(6):200-204.

[2]何友,熊伟.带反馈分布式不同维传感器状态估计技术[J].宇航学报,2003,6(24):574-578.

[3]高蕊,秦超英,张希彬.不同维状态的多传感器MAP航迹融合方法[J].昆明理工大学学报(理工版),2006,3(31):117-120.

[4]熊伟,何友.集中式多雷达系统维数不匹配处理技术[J].系统仿真学报,2003,15(6):845-848.

[5]朱捷,肖慧鑫,吴洪基.基于天球坐标系的异型传感器量测数据分维融合方法[J].兵工自动化,2008,8(27):39-41.

[6]庞志兵.测高雷达与二维雷达数据融合问题研究[J].指挥控制与仿真,2006,28(4):10-12.

[7]王晨熙,王晓博,朱靖,等.雷达与AIS信息融合综述[J].指挥控制与仿真,2009,31(2):1-4.

[8]YAO Jing-shun,YANG Shi-xing .A Modified Multi-data Fusion Method Based on D-S Theory[J].JOURNAL OF CHINA ORDNANCE ,2008 4(4) :278-280.

[9]黄伟平,徐毓.雷达信息站的多雷达数据处理[J].现代雷达,2009,31(2):20-24.

[10]刘彬,胡宇彬,王辉康,等.基于异质多传感器的网络分布数据融合的一种算法[J].传感器世界,2009(30):40-43.