基于交通规则的路网模型建立及最优路径分析研究

杨英伟，饶鸣，殷忠银

(重庆数字城市科技有限公司，重庆 400020)

基于交通规则的路网模型建立及最优路径分析研究

杨英伟∗，饶鸣，殷忠银

(重庆数字城市科技有限公司，重庆 400020)

研究了国内交通规则，建立起了适于最优路径分析的路网数据模型，利用Dijkstra算法实现了两点之间最优路径分析和多点之间最优路径分析，并阐述了最优路径分析在实际中的应用及其重要性。

最优路径；Dijkstra；路网数据模型

随着社会日益发展，科技不断进步，城市现代化进程也在加速发展，“衣、食、住、行”中最后这一要素“行”也越受重视与关注。如何降低油耗，减少时间成本成为驾驶员最为关注的问题。最优路径分析是研究如何在起点到终点间找到一条最优路径的方法，“最优”既可以指距离最短，也可以指成本最低。国内外学者对此问题做了大量研究，其中以Dijkstra算法最为经典。然而最优路径分析不但需要高效的算法，同时还需要准确、高效的路网模型做支撑，才能为驾驶员提供最优路径分析服务。

最优路径分析本质属于图论研究中的一个经典问题，但在实际应用中，需要结合交通规则和道路的实际情况，将其抽象为有实际意义的路网模型，才能应用在实际交通运输中。本文是在研究了现有最短路径算法的基础上，建立了基于交通规则的路网数据模型，实现了最优路径求解，并描述了其在交通运输、物流配送等行业中的应用及价值意义。

1 路网模型

1.1 模型

模型是对客观现实事物的某些特征与内在联系所作的一种模拟或抽象，为了研究一个过程或事物，可以通过提取在某些特征(形状或结构等)方面与它相似的“模型”来描述或表示具体事务。路网模型就是现实世界中路网的客观抽象，真实的反映路网内部结构及关系，以便于在此模型上进行最优路径分析。

道路采集后是由若干连续的点所组成的多边线，其模型如图1所示，其中首尾点称作“结点”，中间点称作“接点”。“结点”表示道路的起始点和结束点，道路与道路之间通过结点相连；接点只代表道路的数字化坐标，不具有表达拓扑关系的功能。

图1 弧段、结点拓扑关系

1.2 路网模型建立

道路建设目的是便于车辆通行，从机械运动学原理上讲，车辆可以在道路上随意行驶。但如果没有交通规则作为行驶准则，车辆杂乱无章的行驶，很难想象会对社会造成多大的灾难，因此国家制定了城市交通规则和相关法律法规，约束驾驶员按交通规则行驶，并在道路路口、路面设置了各种交通标志。路网模型只有严格遵照交通规则，才能真实反映现实道路情况，才能在此模型上做最优路径分析[1]。

为了满足最优路网分析，我们采用表1所示数据结构来描述一条道路。

道路数据结构 表1

?

其中道路类型包含高速公路、主干道、次干道、支路等四种类型；行驶代价既可表示时间代价，也可表示费用代价。系统设计为开放式系统，针对不同用途选择不同的影响因子。例如，考虑行驶时间最快，Cost值如下设置:

P表示道路类型权值，其值由统计分析获得，由于不同城市道路状况不同，P值也会相应不同，道路类型权值P越小，等里程下耗时越短，在耗时最优路径分析下被选中的几率越大；Length表示道路长度，其值除以最长的道路长度MaxLength做均一化变换，以便于分析计算。

图2是重庆市江北区商圈的道路状况，是一个较为复杂的路网系统，其中囊括了立体层次、单行、双行、左转及掉头等道路状况及交通规则，运用上述道路网模型，可抽象为图3所示的道路网模型。

图2 现实路网状态图

图3 现实道路网模型

具有相同结点的道路相连通，双向行驶道路正向行驶代价和逆向行驶代价均为正值，表示其可通行；单向行驶道路，若行驶方向与数字化方向一致，则正向行驶代价为正，逆向行驶代价为负，表示不能通行。根据道路类型，可由公式(1)计算该道路正向行驶代价和逆向行驶代价。表2列举了部分道路的数据结构:

部分道路结构 表2

1.3 路网模型特点

上述模型真实反映了客观世界路网信息，已在系统中验证使用，具体表现在:

(1)实用性:该模型能真实的反映道路的拓扑关系和通行状况，为最优路径分析打下了数据源基础；

(2)可扩展性:针对不同需要，模型可扩展出更多的道路描述信息；

(3)开放性:最优路径有多种含义，包括耗时最短或距离最短等情况，系统可自定义Cost字段值，满足其自身需求。

2 最优路径分析

最短路径是指顶点之间路径最优。抽象到图论中，路网可以看作是有向图，图的顶点表示道路结点，图的边表示道路路段，图的方向表示道路通行方向，边的长度即可表示道路长度，也可表示道路通行时间，根据不同的要求赋予边长以不同的含义。最优路径分析分为两类，一是指从起点到终点之间路径最优，另一种是指从起点到多点之间路径最优，也称货郎担问题。

2.1 两点之间最优路径

Dijkstra[2～4]算法是解决最优路径最经典的算法，其基本思想是:若从点S到点T有一条最短路径，则该路径上的任何点到S的距离都是最短的。该算法适用于一个理想的路网图，在实际路径分析中，需要结合实际使用方式，经过预处理才能进行路径分析，分析结果同样需要经过处理才能呈现给使用者，下面是最优路径分析的主要步骤:

(1)输入起点坐标P1和终点坐标P2；

(2)搜索离P1和P2最近的两条道路L1和L2；

(3)在L1上选择一个结点，作为模型中的起始点PS，在L2上选择一个结点，作为模型中的终止结点PE。若L1为双向行驶，则任意选择FirstNode或LastNode作为PS，若L1为单向正向行驶，则选择LastNode作为Ps，若L1为单向反向行驶，则选择FirstNode作为PS，若L2为双向行驶，则任意选择FirstNode或LastNode作为PE，若L2为单向正向行驶，则选择LastNode作为PE，若L1为单向反向行驶，则选择FirstNode作为PE；

(4)计算Cost值和ReverseCost值，P权值如表3所示；

道路类型权值 表3

(5)根据PS和PE，利用Dijkstra算法做最优路径分析，确定两点之间最佳路径；

(6)路径裁剪，Dijkstra算法计算出的最优路径是从PS到PE之间的最优路径，需要裁剪道路，找到从P1到P2之间的最优路径；

(7)输出。

若只考虑距离最短优先，计算权值P时将式(1)中的P全部置为1；若考虑主干道优先，借用2005年上海市城区典型道路平均速度统计值[5]，P值计算结果如表3所示。图4和图5展示了主干道优先和距离优先的两种最优路径分析结果，路网数据为全重庆市道路数据，以人和立交作为起点到朝天门，分析耗时在600 ms到1 s之间。

图4 主干道优先最佳路径分析结果

图5 距离最短路径分析结果

2.2 起点到多点间最优路径

起点到多点间最优路径是指从起点出发，选择一条最优的路径，经过各目的点一次，且仅经过一次，其实质就是著名的货郎担问题[6]。解决办法有穷举法、最短路标号法、动态规划法等。利用上述路网模型，实现主干道优先最佳路径分析和距离最短路径分析效果分别如图6和图7所示，路径分析以松桥路和金龙路交叉路口作为起点，分别经过龙华大道与松牌路交叉路口、金龙路与嘉洲路交叉路口、金城国际3个目的点。

图6 起点到多点间主干道优先最佳路径分析

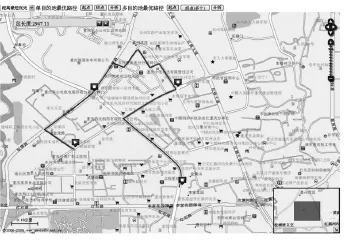
图7 起点到多点间距离最短路径分析

3 最优路径分析应用

交通问题是世界各国面临的共同问题[7]。交通拥挤、绕路等情况造成了巨大的时间浪费，加重了环境污染。由于车辆速度过慢，行驶时间长，尾气排放增加，使得城市的空气质量进一步恶化。交通问题也造成了巨大的经济损失。为了缓解经济发展带来的交通运输发展的压力，尽量的利用现有的资源，使其发挥最大的作用，各国都加大了对智能交通系统的研究和建设的力度。智能交通系统是现代交通运输发展的趋势，智能运输系统(Intelligent Transport System)的主要思想是将传统的交通系统看成是人、车、路的统一体[8]，运用计算机、通信、人工智能、传感器等领域的先进成果来彻底改变目前被动式的交通局面。最优路径分析可以作为智能交通系统的一部分，辅助系统使用者规划最优行车路线，减少出行成本。

在物流配送与选址上，怎样规划配送货车的行驶路线，减少配送时间和降低运输成本，规划选址地点，成为物流公司主要考虑的问题，随着现代物流业的发展，在物流管理系统中引入最优路径分析辅助规划决策，是提升其竞争力的有力工具。

城市建设往往需要铺设各种管道、管线，合理规划最优路线，可以减少管道铺设材料，可以极大的降低建设成本，节约资源。

4 结论与展望

自驾出行逐渐成为民众主要的出行方式，如何减少行驶时间与降低驾车成本是驾驶员关注的话题，城市道路建设滞后与日渐增长的车辆矛盾越发突出，需要合理的规划行车路线，最佳路径分析作为智能交通系统的一部分，对于路径规划起到积极作用。本文在研究了城市交通规则的基础上，建立了适于最优路径分析的路网数据模型，并在此基础上实现了两种方式的最优路径分析，并探讨了其在实际生产生活中的应用。

路网数据采集包含空间数据采集和属性数据采集，数据量很大，采集道路数据是一个非常庞大的工程，并且国内道路建设更新速度很快，需要交通主管部门组织一个专业的数据采集队伍和建立一个长期有效的路网更新机制。路网分析是智能交通系统中一个重要的部分，随着信息化技术的普及，路网分析会受到越来越多的行业关注和使用。

[1]刘云翔.基于城市道路网的最短路径分析解决方案[J].小型微型计算机系统，2003，24(7):1390～1393

[2]乐阳，龚键.Dijkstra最短路径算法的一种高效率实现[J].武汉测绘科技大学学报，1999，24(3):209～212

[3]Benjam in Zhan F.Three fastest shortest path algorithms on real road network’s data structures and procedures[J]Journal of Geographic Information and Decision Analysis，1995，1 (1):69～82

[4]Dijkstra E W.A note on two problems in connection with graphs[J].Numeriche Mathematic 1959，1:269～271

[5]王海鲲，陈长虹，黄成等.上海市城区典型道路行驶特征研究[J].交通环保，2005，26(3)

[6]杜均，蔡之华，朱莉.用遗传算法解货郎担问题[J].微型机与应用，2004，23(10)

[7]刘学军，徐鹏.交通地理信息系统[M].北京:科学出版社，2006

[8]史其信.中国道路交通的现状与ITS研究展望.第一届亚太地区ITS会议(东京)，1996.10

Building Road Data Model Based on Traffic Rules and Researching on Shortest Path Analyzing

Yang YingWei，Rao Ming，Ying ZhongYin
(ChongQing Cybercity Sci－tech Company，ChongQing 400020，China)

This paper studies the domestic traffic rules，and builds a road data model in suit for shortest path analyzing.Using Dijikstra，implements the shortest path analyzing between tow points and among multiple points.Finally，this paper describes the application of shortest path analyzing in practice and its importance.

Shortest Path；Dijikstra；Road Data Model

1672－8262(2010)04－58－04

P208

A

2009—12—02

杨英伟(1983—)，男，软件工程师，现从事WebGIS、地理信息多尺度表达研究。