再议计算子午线弧长的数值积分法

杨双富

(云南一九八煤田地质勘探队，云南昆明 650208)

再议计算子午线弧长的数值积分法

杨双富∗

(云南一九八煤田地质勘探队，云南昆明 650208)

给出了利用复化辛普森(Simpson)积分公式计算子午线弧长的方法，分析了计算结果精度与积分区间的大小和区间等分数的关系。

子午线弧长；数值积分；辛普森(Simpson)积公式、复化辛普森(Simpson)积公式

1 前 言

《测绘通报》2006年第5期刊登的《计算子午线弧长的数值积分法》一文中介绍了子午线弧长计算的数值积分方法，遗憾是的没有明确指出其计算结果源自于数值积分方法中的哪一种，但通过与经典方法结果相对比，得出相互矛盾的结论:“数值积分法与经典方法的计算结果之间存在着显著的差异，数值积分法精度高。”[6]，值得注意是经典方法计算结果的精度优于1 mm，而从文中表1～表3(仅摘录表1)可以看出，纬度从10°～90°，子午线弧长的数值积分法计算结果与经典方法相差750多米到92 680多米，竟不如仅将积分区间二等分的辛普森(Simpson)积分计算结果，真让人匪夷所思。

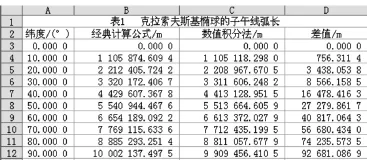
图1 《计算子午线弧长的数值积分法》一文表1摘录

众所周知，数值积分法精度高低与所采用积分方法、积分区间的大小、区间等分数或节点数多少有密切的关系，下面以克拉索夫斯基椭球体及最常用的辛普森(Simpson)积分公式、复化辛普森(Simpson)积分公式为例，对采用数值积分法计算子午线弧长作一简略的分析。

2 子午线弧长计算公式及数值积分公式简介

2.1 子午线弧长计算公式

设a为椭球的长半轴，e为第一偏心率，则在子午圈上从赤道开始到任一纬度B的弧长计算公式为[2]:

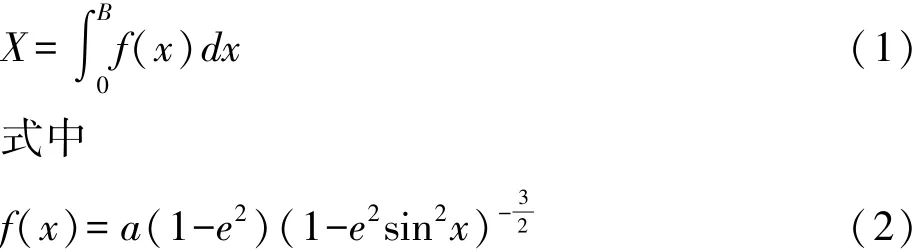
2.2 经典计算公式

式中系数a0、a2、a4、a6、a8详见文献[2]。

2.3 辛普森(Simpson)积分公式

2.4 复化辛普森(Simpson)积分公式

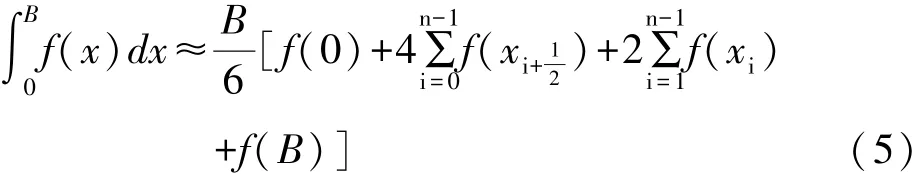
式中n为积分区间等分数。

3 子午线弧长计算结果对比

3.1 子午线弧长计算函数的设计

为方便操作及使用，以Excel 2003为计算平台，采用自定义函数的方式设计各计算函数。启动Excel 2003，选择菜单工具(T)→宏(M)→Visual Basic编辑器(V)或按Alt＋F11进入Visual Basic编辑器，再依次点击插入(I )→模块(M)，添加一个模块，然后输入如下程序:

Public Const pi As Double＝3.14159265358979'定义常数pi (即π)

Public Function jdhcjs(ByVal x As Double)

其中“jdhcjs”、“Simpson”、“Simpson0”三个自定义函数分别对应于子午弧长计算的经典公式、辛普森(Simpson)积分公式和复化辛普森(Simpson)积分公式，而“Deg”是将形如“度.分分秒秒”格式的纬度转换为弧度的函数。

3.2 子午线弧长计算对比

(1)经典计算公式与辛普森(Simpson)积分公式计算结果对比

建立如图2所的表格，在A列3～12行填入纬度0°～90°，分别在B3、C3、D3单元格中填入公式“＝jdhcjs (A3)”、“＝Simpson(0，A3)”、“＝A3－C3”，选中B3～D3单元格，利用填充柄向下填至12行，结果见图2。其中B列3～12行为子午线弧长的经典公式计算结果，C列3～12行为子午线弧长的辛普森(Simpson)积分公式计算结果，D列3～12行为前面两计算结果之差。

图2 计算截图

(2)经典计算公式与复化辛普森(Simpson)积分公式计算结果对比

依照(1)操作步骤建立如图3所示的表格，仅将C3单元格中的公式改为“＝Simpson0(66，0，A3)”，得到的结果如图3。

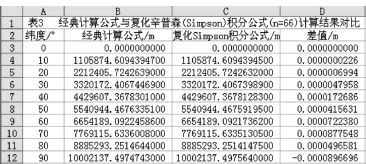
图3 计算截图

(3)复化辛普森(Simpson)积分公式计算精度浅析

建立如图4所示的表格，在第2行B列～J列填入纬度10°～90°，在A列3～14行中填入积分区间等分数n＝20～100，在B3单元格中填入公式＝(jdhcjs(B＄2)－Simpson0(＄A3，0，B＄2))∗1000”，选中B3单元格，利用填充柄向右填至J列；选中B3～J3单元格，利用填充柄向下填至14行，结果见图4。表中B 3～J14区域内单元格中的数值为子午线弧长的经典公式计算结果与复化辛普森(Simpson)积分公式计算结果之差的1000倍。从表中不难看出，当积分区间相同时，随着积分区间等分数的增加，计算结果的精度提高；当积分区间等分数相同时，在纬度10°～60°范围内，随着积分区间的增大，计算结果的精度降低，而在纬度60°～90°范围内，计算结果的精度却呈现不规则变化。

图4 计算截图

4 结 语

通过上面简略分析，与经典方法的计算结果相比，可以看出子午线弧长数值积分法计算结果的精度不仅与所用积分方法有关，而且还与积分区间的大小、区间等分数或节点数多少密切相关，这一点在实际运用中应加以区别对待，如复化辛普森(Simpson)积分公式要获得任意积分区间的计算结果优于1 mm，其区间等分数n至少取66。

[1] 邢永昌，张凤举.矿区控制测量(上册)[M].北京:煤炭工业出版社，1987

[2] 孔祥元，郭际明，刘宗泉.大地测量学基础[M].武汉:武汉大学出版社，2001

[3] 徐萃薇.计算方法引论[M].北京:高等教育出版社，1987

[4] 翟瑞彩，谢伟松.数值分析[M].天津:天津大学出版社，2000

[5] 数学手册编写组.数学手册[M].北京:人民教育出版社，1979

[6] 刘修善.计算子午线弧长的数值积分法[J].测绘通报，2006(5):4～6

Reconsideration of the Numerical Calculation of Radial arc Length Integral Method

Yang ShuangFu
(198 coal geological exploration teams in Yunnan，Yunnan 650208，China)

This paper presents the use of complex－based Simpson(Simpson)integral formula meridian arc length method to analyze the accuracy of calculation results with the integral interval size and range of the relationship between such scores.

radial arc length；numerical integration；Simpson(Simpson)product formulas，complex of Simpson (Simpson)product formula

1672－8262(2010)06－140－03

P226.1

B

2010—02—05

杨双富(1967—)，男，高级工程师，主要从事工程测量工作。