异构传感器网络捷径优化部署问题研究

傅霞玲陈江勇许力殷知越

（1.福建师范大学数学与计算机科学学院，福建福州350007；2.福建省德化陶瓷职业技术学院，福建泉州362500）

1.引言

随着通信技术、嵌入式技术、传感器技术、无线技术的迅速发展和日趋成熟，具有通信能力、计算能力和感知能力的微型传感器节点开始在世界范围内涌现。数目众多的传感器节点，以Ad Hoc方式构成无线传感器网络[1]。无线传感器网络的传感器节点，随机撒播或均匀有规则地分布在监测区域，协同感知、采集和处理网络覆盖范围内的感知对象的信息，并把收集的信息，以多跳的方式发送给汇集节点（Sink节点）。但由于传感器节点由电池供电，电池的容量一般不大，而且其特别的应用领域也决定传感器在使用过程中，很难再充电或更换。因此，节能以延长网络的生命周期是无线传感器网络设计的首要任务[2-3]。

l929年，匈牙利作家F.Karinthy最早提出了“小世界现象”的论断[4]。1998年，Watts和Strogatz对规则网络进行断链重连得到了既具有小世界效应(L～lnN)，又具有集团化特征的网络，提出了著名的W-S小世界网络(Small World Network SWN)这一概念，并建立了模型[5]。2004年，Helmy等学者通过在Ad Hoc网络中引入逻辑链路形成具有小世界效应的无线网络，验证了小世界网络同样适用于具有空间属性的无线网络[6]。Helmy等人还研究了在磁盘网络模型中以静态汇聚节点为中心的无线传感器网络中设置有线链路产生捷径的能量效率问题[7]。

但是，Helmy等人只是分析了有线的最优长度、加入多少的有线后能量效率达到最高，以及最大可以达到的能量节省率，而没有分析这些有线放置的最优位置。因此，本文采用遗传算法，研究在磁盘网络模型中，传感器节点均匀分布的单个Sink节点的静态异构传感器网络中有线捷径的优化部署问题。通过有线捷径的引入，最大幅度地降低平均路径长度，达到提高网络能量效率、延长网络生命周期的目的。

2.网络模型及路由策略

2.1 网络模型

本文采用磁盘网络模型，传感器节点以图1所示的方式均匀分布于网络拓扑中，节点之间信息传输采用曼哈顿距离（Manhattan Distance），每个节点到邻居节点的距离均为一跳。网络中只有一个Sink节点，所有的普通节点都把采集的信息发送到Sink节点。网络为静态及位置相关，即当网络布设完成后，节点将保持位置不变。

在网络中加入有线捷径（wired shortcuts）或中继节点，构造具有“小世界效应”的异构传感器网络。有线捷径一端放置在远离Sink节点的地方，另一端与Sink节点只有一跳的距离、与Sink节点可以直接通信。或者也可以采用具有足够的能量供应、存储和处理能力更强的中继节点，这些中继节点也是与Sink节点只有一跳的距离。两种情况下，都只要确定远离Sink节点的那一端的位置，分析的情况是一样的，因此，在本文的论述中，捷径与中继节点为同义词。

在图1的磁盘网络模型中，从拓扑的中心往外看，共有5个圆，表示一个具有5层的磁盘网络。中心的第一个圆为第1层，从中心往外看，每个圆环分别为第2、3、4、5层。若Sink节点在拓扑中心上，则每一层上的节点，不管是在圆上，还是在该层的圆环内，到Sink节点的跳数是一样的（采用贪婪路由策略）。

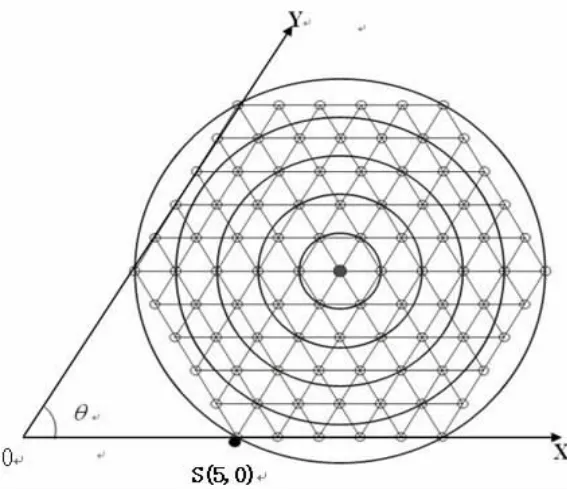
图1 节点均匀分布的5层磁盘网络模型（用θ=60o的斜坐标系表示）

2.2 路由策略

本文采用贪婪路由策略，即某个节点N要发送数据到Sink节点时，它把数据包发送给距离Sink最近的邻居节点，邻居节点再重复这种过程，直到数据包发送到Sink节点。采用贪婪路由算法，数据包以最小的跳数，就可以到达Sink节点。当网络中加入有线捷径时，显然，对于有些节点，通过有线捷径构成的有线链路，可以更快地到达Sink节点，因此，信息通过有线链路，传输到Sink节点；而对于另一些节点，直接通过无线链路，传输距离更近，就不必要通过有线链路了。数据包到底如何传输，需要进行比较判断：

设：用NS（xs，ys）表示Sink节点坐标，Ni(i，j）表示普通节点坐标，Nn(xn，yn)为中继节点坐标。

令：dWSN=|i-xs|+|j-ys|，dHSN=|i-xn|+|j-yn|+1

其中，dWSN表示普通节点通过无线链路到达Sink节点的距离（跳数）；dHSN表示通过有线链路到达Sink节点的距离（跳数）。

若：dWSN＜dHSN，则数据包通过无线链路到达汇集节点；否则，数据包通过有线链路到汇集节点。

3.“捷径”的优化部署及性能指标

3.1 “捷径”的优化部署

传感器网络中节点的能量消耗主要在于数据包的传送和接收过程，整个网络的能耗与网络中所有节点达到Sink节点的总跳数成正比。因此，我们可以在网络的平均路径长度和网络的能耗之间建立对应关系。网络的平均路径长度最小，也即能耗最小。

用L(N)表示在m层磁盘网络模型中，放置n个中继节点后异构传感器网络的平均路径长度。则L(N)为：

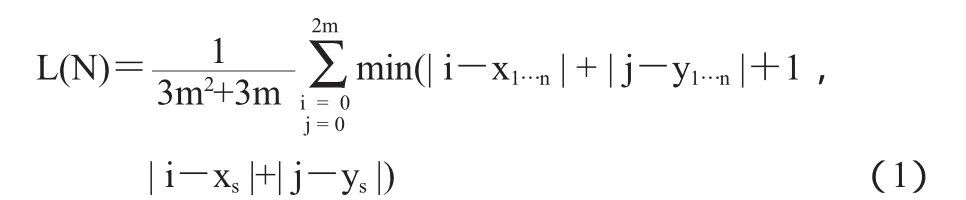
其中：

(i，j)为网络中任一普通节点的坐标

(x1…n，y1…n)为中继节点的坐标

(xs，ys)为sink节点的坐标

由于网络中第一层为6个节点，其余各层的节点数构成公差为6的等差数列，因此，m层磁盘网络的总节点数为：Sm=a1*m+m(m-1)d/2=6m+m(m-1)*6/2=3m2+3m

3.2 网络性能评价指标

用L(O)表示未加线时无线传感网络的平均路径长度，用ESR（Energy Saving Raito）表示加线后网络的能量节省率，则：

由式(3)可知，在网络规模及有线条数确定的情况下，L(O)为一固定值，因此，若要提高网络的能量效率，获得最大的能量节省率ESR，必须是有线得到优化放置，使得L(N)为最小值。可见，用ESR可以很方便地评价网络的性能指标。

4.用遗传算法实现“捷径”的优化部署

4.1 遗传算法

遗传算法是一种模拟自然进化过程发展起来的高度并行、随机、自适应的搜索算法。它从代表问题可能的解集的一个种群开始，而一个种群则由经过基因编码的一定数目的个体组成。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解。在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群[8，9]。

本文采用轮盘赌选择方案，即每个个体串按照它们的适应值进行选择，选择操作通过随机方法来实现。变异也是产生新个体的一种方法，但一般变异概率都非常小，故不是产生新个体的主要方法。通过变异操作可以改变遗传算法的局部搜索能力。

4.2 编码模式及初始种群的产生

本文采用了一种编码映射方法：把所有的节点按坐标从0开始进行编号。对于半径为5的磁盘网络，坐标为(5，0)的节点对应编号0，(5，1)对应编号1，依次类推。所以，半径为m的磁盘网络的所有节点对应一个整数集合Zn={0，1，2，3……，3m2+3m}，这样部署n个中继节点的一个方案就唯一对应Zn的一个包含n个元素的子集，即每个染色体对应Zn的一个包含n个元素的子集。并且，我们在开始的时候随机产生一定数目的Zn的n元子集作为初始种群。

4.3 适应度函数

对生存环境较高的物种将获得更多的繁殖机会，因此适应度值和目标函数值成反比关系，目标函数值越小的个体，其适应度函数值越大，保证以较大的概率被选择交叉产生下一代，适应度函数定义如(4)式所示。

公式中，考虑到取倒数后，值太小，所以用1/L(N)乘以一个系数（3m2+3m），并且再取平方值以拉大各数值间的差距。

5.仿真实验及分析

5.1 仿真环境

实验考虑Sink节点位于最外层第5层圆环上这种较特殊的情况，坐标为S(5，0)。用Visual C++6.0实现仿真，仿真实验数据如下所示。

网络层数M取值：5-20

中继节点个数N取值：0，1，2…10，15，…50

种群大小：30

交叉概率：0.80

变异概率：0.05

遗传总代数：1000

随机数种子：88

算法重复执行次数：5

5.2 仿真结果及分析

5.2.1 中继节点的位置确定且不是唯一解

表1 两种网络规模下中继节点优化部署方案

由表1可知，中继节点的坐标可以获得，因此，采用本方案可以直接确定中继节点的位置，对中继节点可以直接进行部署，并且由于对称性等原因，优化部署方案不是唯一解。

5.2.2 平均路径长度与中继节点的关系

图2 不同网络规模下平均路径长度与中继节点的关系

在图2中，网络规模m增大时，若不加捷径，平均路径长度急剧增大，如图所示，m=5，L(0)=7.7；m=20，L(0)=35.5。但当加入少量的有线后(1-4)，平均路径长度急剧下降，当捷径增加到10时，各种网络规模下的平均路径长度相差不大，说明随着捷径的加入使得平均路径长度大大减小，网络的能耗大大降低。随着有线数量的增加，平均路径长度减小缓慢。这也从另一方面说明，并不是增加越多的有线越好。到底要加多少的有线，既可以较大幅度的降低能耗，又可以兼顾经济效益，这需要在两者之间进行权衡。

5.2.3 能量节省率与中继节点个数的关系

由图3得，当中继节点个数增加到10个时，网络的能量节省率可以达到70-80%；继续增加中继节点个数到25，能量节省率达到77-87%。这与Helmy等人在论文[7]中的结论“加线5-24，路径长度减少60-70%”相比，采用此方案可以获得更高的能量节省率。

图3 不同网络规模下能量节省率与中继节点个数之间的关系

6.结论

本文研究磁盘网络模型的节点均匀分布的异构传感器网络的捷径优化部署问题。理论分析与仿真实验表明，采用遗传算法可以得到优化部署方案，通过最大限度减少网络的平均路径长度，获得最大的能量节省率，从而达到延长网络的生命周期的目的。并且有线的条数和位置确定后，线的长度也即确定，因此，便于网络的布设与管理。

[1]Estrin D，Govindan R，Heidemann J，et a1.Next centurychal1enges：scalable coordinate in sensor network[A].In：Proc.of 5th ACM／IEEEInt’1Confon Mobile Computing and Networking[C].Washington，USA：ACM Press，1999.263～270.

[2]孙利民，李建中，陈渝，无线传感器网络[M].北京：清华大学出版社，2005.

[3]周贤伟，覃伯平，徐福华，无线传感器网络与安全[M].国防工业出版社，2007.

[4]Braun T.Hungarian priority in network theoty[M].Science，2004.

[5]WATTS D，STROGATZ S.Collective dynamics of‘small-world’networks[J].Nature，1998，393：440—442.

[6]HELMY A.Contact based architecture for resourcediscovery(CARD)in large scale MANets[J].IEEE／ACM IPDPS WMAN，2003，(4)：219—227.

[7]HELMY A，CHITRADURGA R.Analysis of short cuts in wireless sensor networks[C].Proceedings of the The IEEE/ACS International Conference on Pervasive Services(ICPS'04)，July 19-23，2004：167-176.

[8]王小平，曹立明，遗传算法---理论、应用与软件开发[M].西安交通大学出版社，2002.

[9]Zhao Chunhua，Yu Zhiqiang，Chen Peng.Optimal deployment of nodes based on genetic algorithm in heterogeneous sensor networks[C].2007 International Conference on Wireless Communications，Networking and Mobile Computing，WiCOM，2007：2743-2746.