水平轴风力机叶片翼型结冰的数值模拟
邓晓湖,卢绪祥,李录平,李海波
(长沙理工大学能源与动力工程学院,能源高效清洁利用湖南省普通高等学校重点实验室,湖南长沙410114)
风力机组一般安装于高寒、沿海地带,风力发电机的浆叶经常会出现覆冰现象,导致桨叶的性能以及风力机功率的输出达不到设计要求。风力机叶片的结冰是由过冷水滴撞击叶片表面后冻结成冰覆盖在叶片表面形成的。在结冰过程中若撞击到叶片表面的水滴立即冻结,生成的冰型就比较规则,称为霜状冰;若表面大部分区域的水滴不能立即完全冻结,未冻结的水就会在气流驱动下沿表面流动,并在流动过程中逐渐冻结,形成的冰称为瘤状冰[1]。叶片的结冰影响风力机的气动性能和运行安全,给风力机带来极大危害。例如,覆冰会改变叶片的外部形状和气动性能,增大叶片阻力、减少升力,影响全机操纵性、稳定性;最终导致风能的转化效率降低,严重的可导致叶片的损毁,发生运行事故,风力机叶片结冰已经成为保证风力机安全运行需要解决的迫切问题。早期对风力机结冰进行的研究都采用实验的方法,例如Bose等人在1992年对处于寒冷气候中的双叶片水平轴风力机结冰进行了测量,但是并未指出结冰形状和外部结冰条件的关系[2-3];Jasinski等人在1998年对NREL-S809翼型进行了冰风洞实验,得出了该翼型结冰前后的性能参数[4],但是实验的方法非常麻烦。目前计算流体力学(CFD)的模拟已经应用到了风力机叶片结冰模拟中,采用模拟方法对风力机叶片翼型结冰的研究通常分为三类[5]:对特定条件下的翼型结冰过程进行预测、对已知结冰形状的翼型进行性能预测以及防冰除冰技术研究。不过国内这方面工作尚处于摸索阶段,而且大多借鉴于对飞机机翼和输电电缆结冰的相关研究经验。本文将进行的是第一类研究,通过数值计算方法预测相关厂家提供的风力机叶片翼型前沿霜状冰的形状和增长过程,分析结冰对翼型绕流及气动特性的影响。
1 求解过程
采用数值方法模拟叶片结冰一般分三步[6]:首先,求解流体力学的基本方程组从而得到物体绕流的流场解;其次,把流场解的结果作为定解条件进一步求解水滴的运动方程,从而确定水滴与物体的碰撞点;最后,按照一定的增长模型来确定与物体相碰撞的水滴的结冰以及冰的增长。
1.1 流场计算
采用SIMPLE算法来求解二维定常不可压粘流的时均N-S方程:
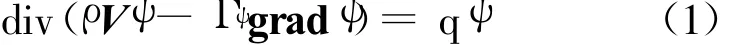
连续方程可表示为:
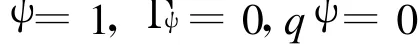
x方向的动量方程可表示为:
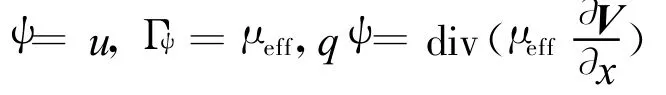
y方向也有类似的表达式。
各项的具体表达式和方程的详细求解方法参见文献[7]。
1.2 水滴轨迹运动方程的求解
用CFD的方法进行翼型结冰数值模拟时,必须对每个水滴进行跟踪,以确定水滴是否与翼型发生碰撞。在计算水滴轨迹时候做如下假设[8]:①水滴的体积保持不变 ,但是水滴的形状可以改变 ,引入与水滴体积相等的当量球的概念,当量球的直径为d eg;②水滴的密度在整个过程中保持不变;③水滴的初始速度与自由流的速度相等,水滴体积很小以至于它们的绕流不会影响流场的性质。水滴轨迹运动方程可以写成[6]:

式中:Md为水滴质量,ρd是水滴密度,ρa是空气密度;V d是水滴体积;g是重力加速度;A d是水滴迎风面积;C d是阻力系数;u代表当地气流速度;u d表示水滴速度。
整理得:
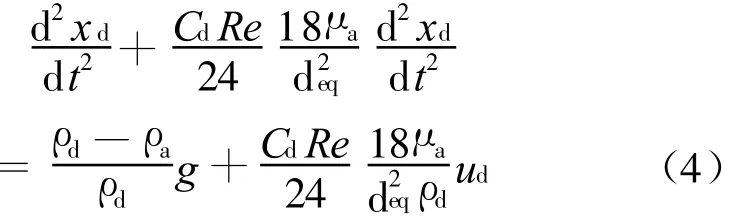
上式为二阶常微分方程,可以把它写成:
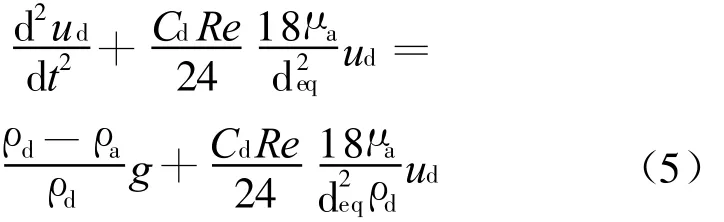
基于流场的速度分布所给定的初始条件,很明显,轨迹运动方程的求解可以看成是一个一阶常微分方程的初值问题:
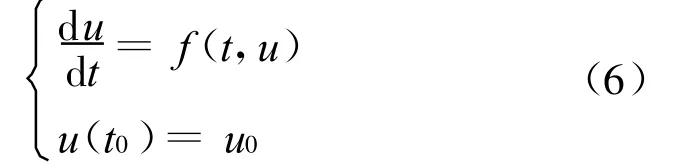
可以采用四阶龙格-库塔法求解,最常用的公式是[8]:
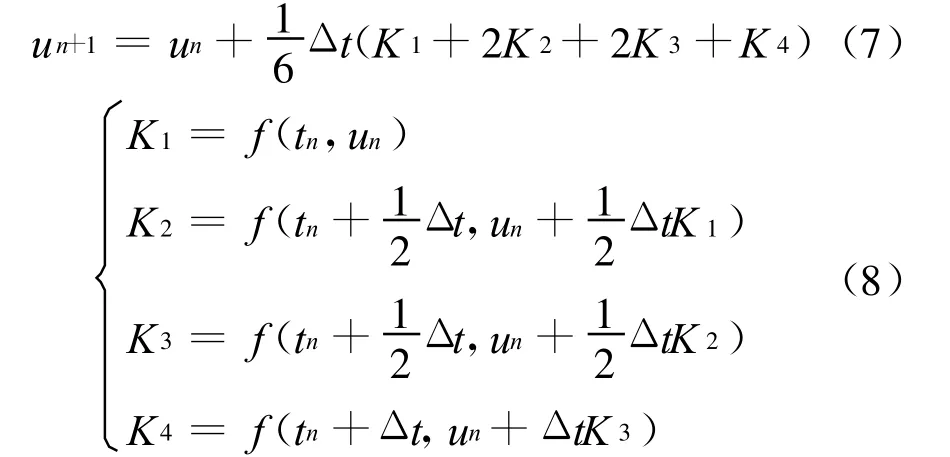
当得到t时刻水滴的速度分ud(t),νd(t)后,则t+Δt时刻水滴的位置可以表示为:
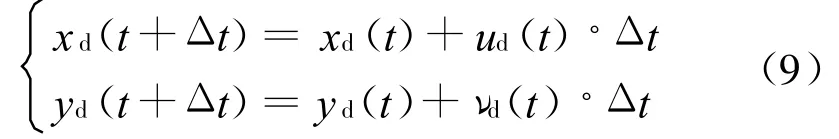
开始计算时,首先给定水滴的初始位置,然后计算Δt时间后水滴的新位置。对于每一个水滴要分别跟踪,如此推进计算,直到水滴与翼面相碰撞或者水滴移出界定区域。
1.3 霜冰厚度的计算模型
对于霜冰情形,由于所有的水滴在碰撞时刻就完全凝结并且不再融化,所以可以不考虑相变热传导等能量导致的变化,只考虑质量平衡就已经足够[9-10]。
图1给出了进入微元控制体中的质量流;微元控制体收集的液态水的质量m1;微元控制体内冻结的水的质量m2。微元控制体的质量平衡方程为:

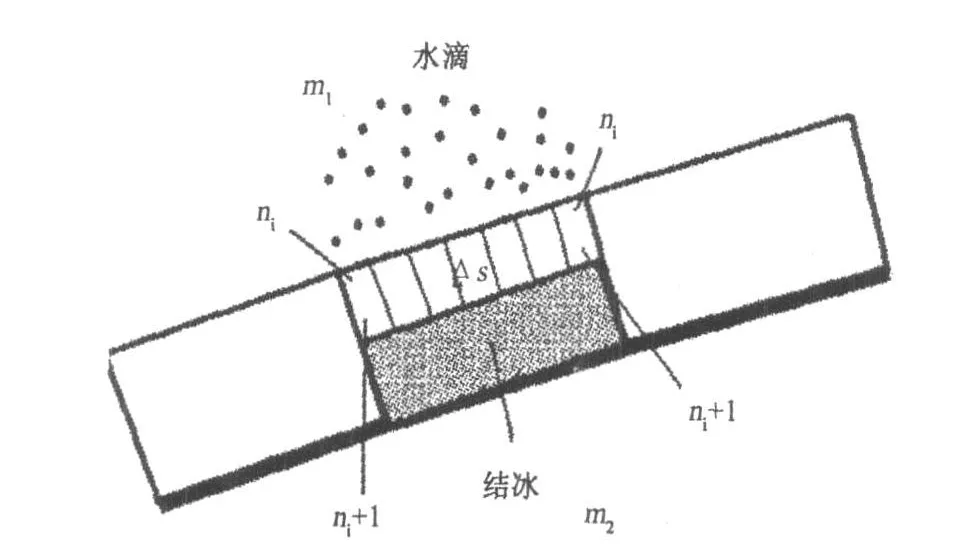
图1 有限容积内质量平衡示意图
将翼型表面分割成很小的一块块区域,这些小区域的面积就是在翼型表面上所对应的弧长。前面由水滴运动方程的求解已经计算到了某个水滴与翼型相碰撞的位置,当水滴碰撞到某个编号为“i”的区域之内时,在计算程序处理中,令该区域所接收到的水滴数量上加1,即:

跟踪计算完每个水滴后,最后撞击到翼型上弧长为d si的一小区域之内的水滴总数即为ni[11-13]。根据质量守恒,冰的密度为300 kg/m3,水的密度为1000 kg/m3,则在已经编号的区域之内,可得:
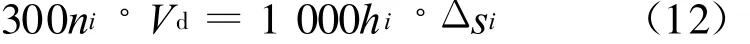
式中:V d是单个水滴的体积;hi是弧长为 Δsi的区域上的结冰厚度。
单个水滴的体积为:

将式(19)带入式(18),则可以得到:
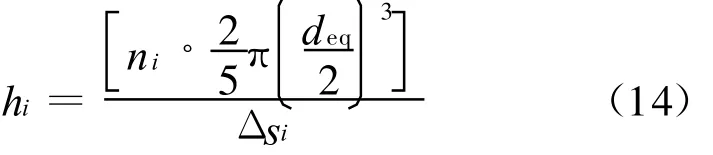
2 结冰计算结果分析
当翼型形状有一定程度的改变后,又对新的结冰翼型的绕流流场重新进行计算,以某厂家自主研发提供的翼型作为结冰表面,然后求解水滴轨迹运动方程和积冰厚度,如此反复迭代,直到需要的时间为止。
本文中所模拟的风力机叶片参数和结冰气象条件为:自由来流马赫数Ma为0.029,风速取固定的10 m/s,时间 T1和 T2分别为6 m in和10 m in,雷诺数Re为2.6×106,环境压力Ph为101300 Pa。环境温度T h=-10℃,冰密度取300 kg/m3;叶片长3.75 m,攻角AOA为0°,水滴有效平均直径M vd为20μm,液态水含量LWC为1 g/m3,假设冰层与翼面间绝热。

图2 翼型一定时间后的积冰形状
图2的(a)和(b)分别给出了6min和10min时风力机桨叶翼型的积冰分布的计算结果。由于翼型前沿的绕流,水滴大部分凝结在翼型的下部,从图中可以看出,在上下结冰极限附近由于撞击到结冰表面的水立即冻结,产生的冰形在滞止区域具有最大厚度,同时冰形比较规则,和文献[2-3]的结果大致相符合。但是从图中还可以看出,由于温度原因,撞击到翼型表面的过冷水滴还会有少量未完全冻结,这些未冻结的水会沿着冰面产生回流,然后再逐渐冻结,以至在滞止区下游形成棱角。总之,在霜状冰结冰预测方面,本文所预测结果与文献结果总体趋势一致,说明本文的预测方法是有效的,预测结果对风力机防冰除冰以及除冰装置的布置具有指导作用,同时也可以在此基础上对风力机叶片在恶劣条件下气动性能进行研究。
3 结冰翼型的气动模拟
3.1 控制方程与边界条件
流场的连续方程:
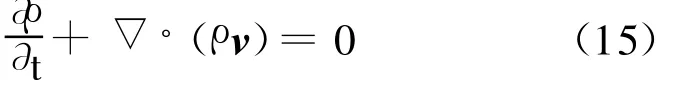
动量方程:

能量方程:
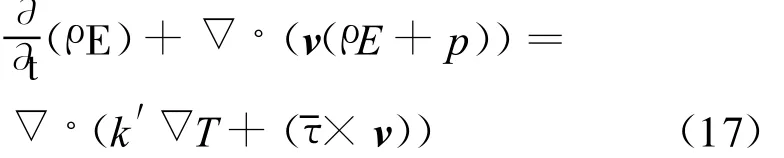
上面三个公式中ρ为空气密度,v为速度矢量,t为时间,p为压强为应力张量,E为内能,k′为热传导系数。
在对控制方程做雷诺平均后得到雷诺平均的NS方程,并采用最佳湍流模型,用于结冰计算。
3.2 湍流模型
本文选择最为适合的Spalart-A llmaras湍流模型。该模型最早被用于有壁面限制情况的流动计算中,特别在存在逆压梯度的流动区域内,对边界层的计算效果较好,因此经常被用于流动分离区附近的计算,通过模型与壁面函数配合可以适用于网格比较粗糙的算例,并且可以在网格精度不高时得到比较精确的解。SpalartA llmaras模型的求解变量是,表征出了近壁区域以外的湍流运动粘性系数。的输运方程为:
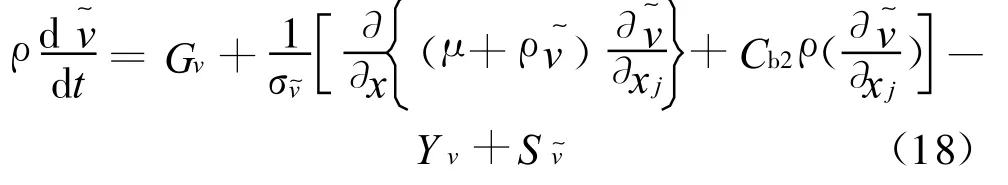
其中Gv是湍流粘性产生项;Yv是由于壁面阻挡与粘性阻尼引起的湍流粘性的减少是用户自定义源项和是常数;v是分子运动粘性系数。湍流粘性系数用如下公式计算:
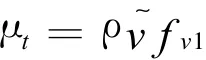
3.3 网格生成
在得出翼型结冰边界后,对新边界进行网络划分进而对其气动性能进行分析和对比。计算中采用Hilgenstoke法生成技术生成计算网格。根据数值计算的需要,采用分区网格的技术和思路,利用各自的优势和特点,生成贴体、与边界正交的、适合N-S方程计算的高质量网格,并对网格疏密及光滑性进行适当控制。在对结冰后翼型进行网格划分时可能会出现尖角或波动扭曲,这会对网格生成及数值计算带来困难,采用保证控制体结冰量不变的原则,对新生成的边界进行光顺处理,图3为结冰后网格形状。
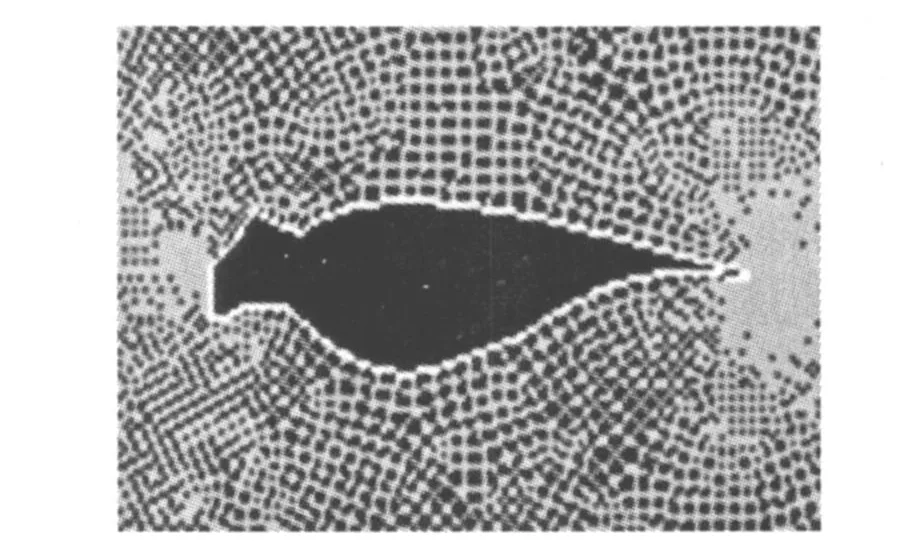
图3 结冰翼型网络划分
数值CFD模拟计算中,采用压力基耦合求解器,对来流采用远场边界条件;并且在初始化时使用Full M ultigrid(FMG)初始化,以获得更好的初始流场数据。计算基于RANS方法,采用二维稳态分离解法的隐式解法,空间离散格式采用二阶迎风格式,压力—速度耦合采用SIMPLE解法。所采用的边界条件为:固壁表面采用无滑移条件、进口、出口和Interior面由特征相容条件所确定、计算边界由插值确定。

图4 结冰翼型表面速度分布
图4为结冰翼型翼面附近流场的速度分布的模拟结果,可以明显的看出,由于翼型前缘积冰的不规则,翼型上的速度分布非常不均匀。这种不均匀的速度分布对翼型后部气流形成持续干扰,最终增加了整个翼型边界层的不稳定性,促使叶片上的流动提前分离,从而导致翼型压差阻力增大,阻力系数也随之增大。此外,翼型前缘不规则的冰型增加了翼型的表面粗糙度,从而增加了翼型的摩擦阻力。
4 结冰翼型气动模拟结果分析
4.1 结冰翼型的表面压力
图5的(a)和(b)分别是6 m in和10 min时光洁翼型和结冰翼型的压力分布对比曲线,图中只对结冰翼型进行了标明。由光洁翼型的压力分布曲线可以看出,在翼型上表面沿着曲线由前缘点至后缘点方向静压值变小,但是变化趋势较平缓;在翼型下表面沿着翼型曲线由前缘点至后缘点方向静压值增大,变化曲率也较大,即变化较为迅速。将两种积冰翼型的压力分布曲线与光滑翼型进行比较,可以看出积冰后在下翼面压力系数峰值附近,曲线的下降忽然变陡并出现振荡,上翼面压力系数前沿有所减小,因此,翼型前沿气动特性已经被破坏,随着结冰厚度的加剧,破坏也越明显。
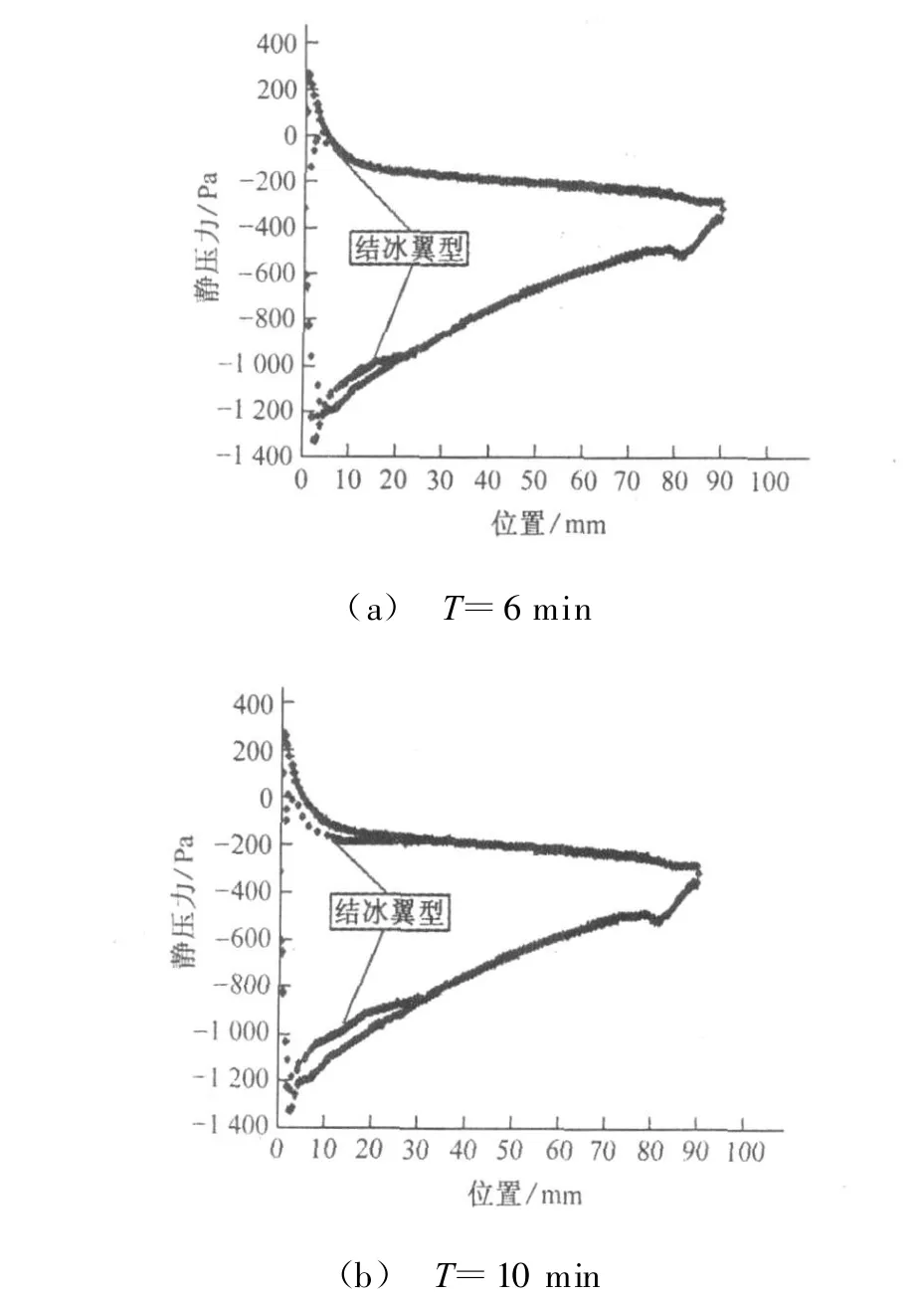
图5 翼型的压力分布曲线
4.2 结冰翼型的升阻力系数
图6和图7分别给出了翼型在洁净和结冰状态下的升阻力系数对比曲线,可以看出结冰翼型的升力系数普遍低于干净翼型,在模拟气象条件下,桨叶最大升力系数由原来的1.1876下降到了0.8642,下降了27.23%。同时,结冰后翼型的失速发生在攻角为11°的时候,比干净翼型的15°提前了4°,也就是说结冰翼型比干净翼型提前失速。由阻力系数可以看出,翼型前缘带冰会增加风力机叶片的阻力。阻力系数平均增加了38.65%,特别是失速攻角大幅度下降,对阻力特性的影响最大,提前进入失速区也是导致阻力系数增大的主要原因。
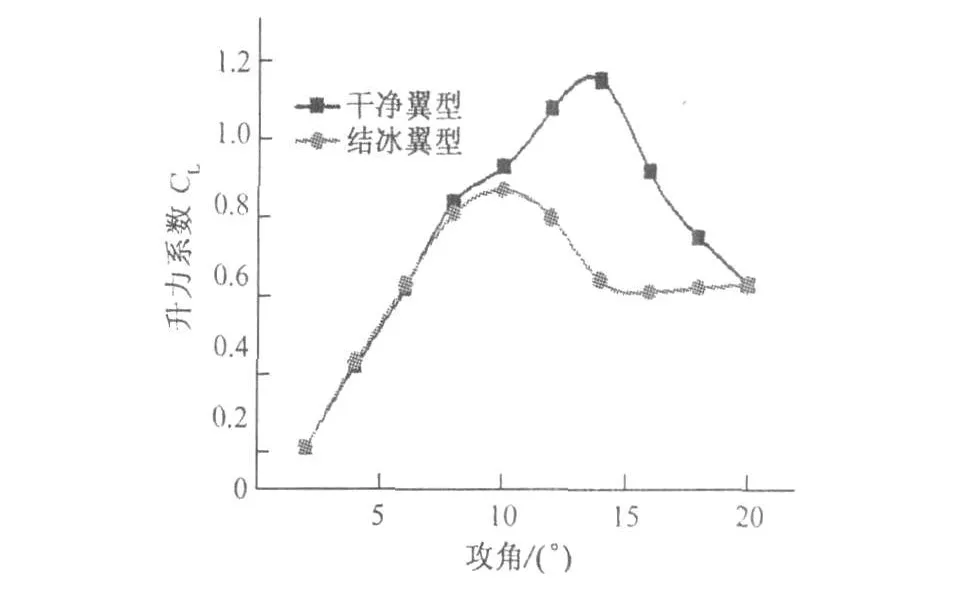
图6 翼型升力系数对比曲线

图7 翼型阻力系数对比曲线
5 结论
本文采用四阶龙格-库塔法求解水滴运动轨迹,并且采用了全N-S方程对风力机叶片翼型的积冰进行了预测,之后利用FLUENT软件模拟了风力机叶片翼型结冰后周围流场的变化,并且与结冰前叶片翼型的气动性能进行了对比。
(1)采用求解水滴轨迹的方程和结冰厚度计算模型的方法可以有效预测翼型的积冰发展过程和形状,表明这种方法正确有效。
(2)对于风力机叶片的翼型来说,由于前沿发生的绕流,结冰现象大部分是发生在翼型前沿的下部,这和飞机翼型的结冰结论相吻合。
(3)通过对比升力阻力性能,发现模拟气象条件下的结冰翼型与干净翼型相比,结冰翼型的最大升力系数大约减少了27%,阻力系数增加了约38%,失速攻角降低了4°。结冰后翼型提前进入失速区是造成气动性能恶化的主要原因。
[1] MAKKONEN L,LAAKSO T,MARJANIEM IM,et al.Modelling and p revention of ice accretion on wind turbine on w ind turbines[J].W ind Engineering,2001, 25(1):3-21.
[2] BOSE N.Icing on a small horizontal-axis w ind turbine-part I:glaze ice profiles[J].Journalofw ind Engineering and Industrial Aerodynam ics,1992,45:75-85.
[3] BOSE N.Icing on a small horizontal-axis w ind turbine-part II:three dimensional ice and wet snow formations[J].Journalof Wind Engineering and Industrial Aerodynam ics,1992,45:87-96.
[4] JASINSK IW J,NOE S C,SELIG M S,et al.Wind turbine performance under icing conditions[J].Journal of So lar Energy Engineering,1998,120:60-65.
[5] ADDY H E,POTAPCZUKJR M G,SHELDON D W.Modern Airfoil Ice Accretions[R].AIAA-97-0174,1997.
[6] 易贤等.翼型结冰的数值模拟[J].空气动力学学报, 2002,20(4):428-433.
[7] ZHU Guolin,K ronstam.The Calculation of ground effect on a car flow field using tw o dimensionalNavier-Stokes equations[J].A cta Aerody Nam ica Sinica, 1993,11(1):.
[8] 韩凤华.飞机机翼表面水滴撞击特性计算[J].北京航空航天大学学报,1995,21(3):18-21.
[9] FU P,FARZANEH M,BOUCHARD G.Tw o-dimensional modeling of the ice accretion p rocess on transm ission line wires and cables[J].Cold Regions Science and Techno logy,2006,46(3):132-146.
[10] 李岩,田川公太郎.叶片附着物对直线翼垂直轴风力机性能的影响[J].动力工程,2009,29(3):292-296.
[11] MAKKONEN L,LAAKSO T,MARJANIEM I M, et al.Modelling and prevention of ice accretion on wind turbines[J].Wind Engineering,M ulti-Science Pub lishing Co Ltd.,2001,25(1):3-21.
[12] HOCHART C,FORTIN G,PERRON J.W ind turbine performance under icing conditions[J].Wind Energy,2008,11:319-33.
[13] WANG Kevin.Convective heat transfer and experimental icing aerodynam ics of wind turbine blades[D]. Winnipeg,Canada:University of Manitoba,2008.

