渐开线磨削中的非等分直线段逼近算法

王 健，李郝林

WANG Jian, LI Hao-lin

（上海理工大学 机械工程学院，上海 200090）

渐开线磨削中的非等分直线段逼近算法

Non-attainment straight linear impending algorithm on involute grinding

王 健，李郝林

WANG Jian, LI Hao-lin

（上海理工大学 机械工程学院，上海 200090）

为了保证齿轮渐开线磨削的质量，本文研究了渐开线磨削中的非等分直线段逼近算法。文末通过齿轮成型磨削的例子，证明了所提出方法的有效性。

数控加工；非等分线段；渐开线磨削

0 引言

齿轮成型磨削是齿轮精密加工的一种常用方法，这种加工方法要求将砂轮修整为齿轮的齿廓形状，通过砂轮的往复运动完成齿轮的磨削加工[1]。由于一般数控系统只具有直线插补和圆弧插补功能，因此在齿形渐开线线磨削时，一般需用直线插补或圆弧插补算法，在保证一定的加工精度前提下，对于渐开线线进行逼近计算，常用的算法有等插补段法、等插补误差法、三点圆法等[2]。对于渐开线磨削，首先需要解决渐开线的光顺处理问题，非等分直线段逼近算法总体上一阶光滑，易于局部处理，可直接利用数控系统的直线插补功能等，本文根据渐开线磨削的特点，重点研究了非等分直线段逼近算法，并将这一算法应用于齿轮的成型磨削之中。

1 渐开线的非等分直线段逼近算法

以齿轮压力角a为变量，齿轮齿形的渐开线方程为

如图1所示，假设齿轮渐开线压力角为0～20º，OXY为坐标系，曲线OP为齿轮的渐开线轨迹。连接O、P两点，则计算曲线OP与直线OP之间的最大距离Dmax，设其为D1。由于实验中所采用的是Hiwin直线电机，精度可以达到1μm，考虑到温度等因素的影响，最大距离要低于1μm。当然，若希望直线段逼近渐开线更加精确光滑，最大距离越小越好，但同样会增加计算量。很明显，计算得到的D1要远远大于1μm。

图1 渐开线OP轨迹与直线OP间的距离

此时，重新连接O与渐开线中点P1，得到直线段OP1，计算渐开线部分曲线OP1与直线段OP1之间的最大距离，一个新的Dmax，设其为D2。如图2所示。

D2若大于1μm，则重复上述过程，取部分渐开线OP1的中点P2，连接O与P2，找最大距离D3，周而复始，直到Dn小于1μm。这时确定了第一直线段OPn+1。然后连接Pn+1与P两点，计算最大距离并与1μm比较，如图3所示。

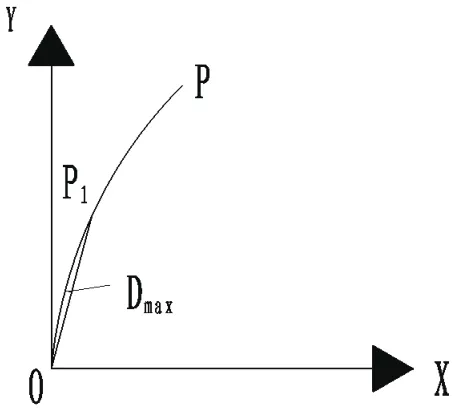
图2 部分渐开线OP1轨迹与直线OP1间的距离

图3 部分渐开线Pn+1P轨迹与直线Pn+1P间的距离

图4 渐开线所有分段

2 算例

实验采用台湾Hiwin直线马达，直线度可达3-10um，X轴最大6m、Y轴0.5m行程，以线性滑轨架构之定位平台，Z向震动可达奈米等级以下，最大速度可达5m/s ，标准重现精度1um或以下，位置回馈系统解析度最低可达50nm。实验仪器如图5所示。

图5 实验仪器

本文应用所提出的方法在上海机床厂有限公司齿轮成型磨削中得到了验证。所磨削的齿轮参数为模数m=5，齿数z=13, 分度圆压力角α=20 º，对于该齿轮的渐开线磨削，在逼近误差为1μm时，需要40段直线段进行逼近。而应用上述的非等分直线段逼近算法，则只需要17段直线段即可满足逼近误差。 Dn值如表1所示。

表1 17段直线段的Dn值

3 结论

本文结合磨削加工的要求以及数控系统只能进行直线插补和圆弧插补的情况，研究了非等分直线段逼近算法。所提出的方法通过齿轮成型磨削中渐开线的磨削，证明了其有效性。同时，本方法还适合具有方程的任意自由曲线，

[1] 李郝林,陈飒,华俭.齿轮成型磨削齿形误差在线测量技术[J].计量学报,2005,4:125-127.

[2] 李郝林,方键.机床数控技术[M].北京:机械工业出版社,2001.

TP273

A

1009-0134(2010)11(上)-0055-02

10.3969/j.issn.1009-0134.2010.11(上).18

2010-03-27

上海科学技术委员会资助项目（08110511600）

王健（1985 -），男，河北石家庄人，在读硕士研究生，研究方向为精密测试与控制。