基于遗传神经网络的电容称重传感器非线性补偿方法＊

俞阿龙

(淮阴师范学院电子与电气工程系，江苏淮安 223300)

0 引言

传感器广泛应用于各行各业，它的误差大小直接影响到测控系统的性能和测量准确度。现代测控系统对传感器的准确度、稳定性和工作条件提出了很高的要求，希望输入与输出特性成线性关系。目前，电阻应变式称重传感器在电子衡器中广泛采用，但是受应变极限的限制，电阻式传感器的金属应变丝电阻的相对变化一般低于1%，且应变丝的阻值受温度的影响很大。与之相比，电容式传感器电容值的相对变化量可大于100%，因此测量范围大得多;电容式称重传感器一般用金属作电极，以无机材料作绝缘支承，因此能承受很大的温度变化。另外电容式称重传感器还具有灵敏度高、动态响应时间短、机械损失小等优点。但在利用电容式称重传感器进行称重测量时，传感器输出电压值与载荷质量之间的关系是非线性的。为了保证一定的测量精度及便于在测控系统中应用，必须对其进行非线性补偿[1－8]。目前常用补偿方法有

①硬件补偿法，该方法难以做到全程补偿，且存在补偿电路硬件漂移问题。

②多项式拟合法，该方法算法较复杂，且拟合准确度常常受限。

③建立传感器的分度表，通过查表产生输出，但是，因为存储器容量的限制，无法得到较高的准确度。

④人工智能法，这是近几年兴起的新方法，具有使用的样本数少，鲁棒性好，可在线补偿等优点，在微机化的智能仪器和控制系统中，有良好的应用前景。目前，国内外相关文献中已有选用BP神经网络对称重传感器的非线性补偿的报道[2，6－7]。但BP神经网络全局搜索能力差、收敛速度慢，结果易陷入局部极值，单独使用神经网络效果不是很理想。而遗传算法(Genetic Algorithm，GA)是一种基于群体进化的随机化全局优化搜索算法，它的搜索始终遍及整个解空间而又不依赖于梯度信息，并且鲁棒性强。但它的局部搜索能力却不足，而且研究表明，遗传算法可以用极快的速度达到最优解的90%左右，但要达到直正的最优解则要花费很长的时间。因此，首先采用遗传算法对神经网络的结构和参数进行快速优化，在解空间中定位出一个较好的搜索空间，并将此作为其后采用神经网络搜索的初始值，然后，利用神经网络的局部搜索能力在这个小的解空间中搜索出最优解。

本文应用基于GA优化的径向基函数 (Radial Basis Function，RBF)神经网络(Neural Network，NN)[9－15]对电容称重传感器进行非线性补偿，从而使传感器与神经网络组成的系统线性化，这不仅提高了计算准确度，而且可实现在线软补偿，鲁棒性好，学习速度也比其一般算法快得多，因此有效地提高了传感器的使用性能与应用范围。

1 电容称重传感器非线性补偿原理

电容称重传感器非线性补偿原理主要基于图1所示的基本环节。设传感器的输入载荷的质量为 m，输出电压为 u，u=f(m)为非线性关系。若在传感器后串联一个补偿环节，使 y=f1(u)=km，那么就实现了传感器的非线性补偿，当k=1时，y=m=f1(u)称为传感器的逆模型。

图1 传感器与补偿环节

RBFNN是一种特殊的三层前向网络，它具有非线性可分的模式空间映射到线性可分状态空间的特性，它在逼近能力、分类能力和学习速度等方面均优于BP神经网络。典型的径向基函数网络的结构如图2所示，它包括一个输入层、一个隐层和一个输出层，输入层和隐层直接连接，隐层包含一系列径向基函数，通常为同一类型。本文中取常用的高斯型函数，将RBF网络用高斯型函数表示为[16]

式中 i表示第 i个隐含神经元，i=1，2，…，N，隐含神经元个数为N;x表示网络的输入向量，ci表示第 i个隐元的高斯分布曲线的作用中心，βi＞0为第 i个隐元的宽度;y为输出向量，Φ=[φ1，φ2，…，φN]T为隐层输出向量;W为权值向量。

图2 径向基函数网络的结构图

对于电容称重传感器来说，将电容称重传感器输出电压 u作为RBFNN的输入训练样本，与电容称重传感器输入对应的线性化质量(km)作为RBFNN的输出训练样本。RBF神经网络模型中隐层神经元的变换函数为高斯函数，而输出层神经元的变换函数采用线性函数。采用遗传算法优化RBFNN的结构和参数，从而得到电容称重传感器的RBF神经网络非线性补偿模型。

2 遗传算法优化RBF神经网络的原理

采用遗传算法优化RBF神经网络的结构和参数，将RBF神经网络的拓扑结构、连接权重、阈值、隐节点中心参数和宽度参数看成一个整体，编码为染色体。选择适当规模的种群，通过遗传迭代逐渐优化，求得网络参数和隐节点数同时优化的结果。基于RBF网络的结构特点，对于给定的电容称重传感器非线性补偿问题，因其输入与输出关系是确定的，因此优化拓扑结构只需确定隐层节点数。本文采用二级递阶染色体结构描述网络结构和参数，其中控制基因表示隐层节点[19]。

对于本文遗传算法优化问题，控制基因用二进制编码，由于RBF网络参数比较多，故参数基因采用实数编码;群体规模取80;因为要对RBF神经网络参数和拓扑结构同时优化，所以定义适应度函数为:

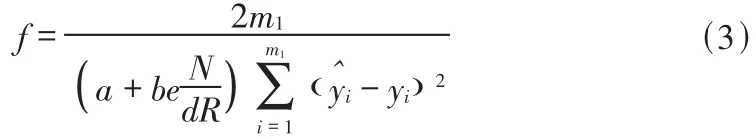
m1——总的学习样本数

N——隐节点数

R——网络输入节点数

a，b，d——常系数[14]

按轮盘赌法进行优质个体的选择;对控制基因串采用单点交叉，参数基因的交叉操作采用线性组合方式，即将两个基因串对应交叉位的值相组合生成新的基因串;对控制基因，变异操作以一定的概率对变异位进行反运算，对参数基因，采用偏置变异，以一定的概率给变异位基因加一个从偏置区域中随机选取的数值。

3 电容称重传感器非线性补偿的实现

要获得电容称重传感器称重系统静态非线性误差补偿网络的学习样本点和检验样本点，需要多次对该称重系统的加载重量和输出值进行实际的测量，即用标定设备对电容称重传感器进行标定实验。

表1为某电容式称重传感器的一组标定实验数据[1]，其中，m为传感器输入载荷的质量，u为其输出电压值。将表1中传感器的31个输入输出测量数据归一化后作为网络的训练样本，用RBFNN建立电容称重传感器非线性补偿模型(逆模型)。取训练网络的初始隐层节点数为35，种群规模为80，交叉概率为0.5，变异概率为0.001。经过150次遗传迭代，得到网络的有效隐层节点为25，误差函数值为

表1 某电容称重传感器的输入由输出测量数据

图3为基于GA优化的RBF网络的训练曲线，图4为基于GA优化的RBF网络补偿与理想补偿曲线。用测试样本对训练后的RBF补偿网络进行检验，得到的预测结果与实际实验值非常相近，误差很小。这表明RBF神经网络具有很强的泛化能力。经补偿，在所有测量点上的相对误差最大不大于0.15%。由此可知，由遗传算法优化的RBF网络补偿模型有高的精度。图5所示为补偿后电容称重传感器输入与输出关系曲线。由图5可知，输入与输出呈良好的线性关系。

图3 基于GA优化的RBF网络的训练曲线

图4 基于GA优化的RBF网络补偿与理想补偿曲线

图5 补偿后电容称重传感器输入与输出关系曲线

4 结论

本文从电容称重传感器输出与输入成非线性关系的现实状况入手，在测试系统中加入了非线性补偿环节，利用遗传神经网络进行非线性补偿。测试结果表明在电容式称重传感器的工作范围内，通过非线性补偿后，测量相对误差小于0.15%，可以满足正常的称重需要，电容式称重传感器的补偿结果令人满意。利用本文提出的遗传神经网络对电容称重传感器进行非线性补偿的特殊优点是能同时优化网络结构和参数，补偿精度高，而且是全局寻优，有良好的鲁棒性，并可实现在线软补偿。将先进的智能方法应用于实际传感器电容称重传感器系统中非线性补偿中，为提高传感器性能开辟了新途径，在测控领域中具有实用价值。

[1] 谢煌，杨三序，李晓伟.基于反拟合法的电容称重传感器非线性校正[J].仪器仪报，2007，28(5):923～927.

[2] 严洁，赵研，张俊.利基于BP神经网络的称重传感器静态非线性误差补偿研究[J].传感 技术学报，2008，21(6):1025～1028.

[3] 刘天键，王劭伯，朱善安.基于神经网络的铂电阻温度传感器非线性校正方法[J].仪器仪表学报，2002，23(5):518～521.

[4] 吕新明，孙海峰，马艳娥.基于函数链神经网络的热电阻非线性校正[J].化工自动化及仪表，2003，30(3):79～81.

[5] 陈俊杰，卢俊，黄惟一.基于遗传神经网络的传感器系统的非线性校正[J].仪器仪表学报，2003，24(2):201 ～204.

[6] Patra J C， Kot A C， Panda G.An intelligent pressure sensor using neural networks[J].IEEE Trans.Instrum.Meas.2000，49(8):829 ～ 834.

[7] Patra J C， Gopalkrisshnan V，Angee L， et al.Neural networ－based self－calibration/compensation of sensors operating in harsh environments.Sensors[J].Proceedings of IEEE，2004，50(1):425～428.

[8] Pereira J M D，Girao P M B， Postolache O.Fitting transducer characteristics to measured data[J].IEEE Instrum.And MEAS.，2001，50(12):26 ～ 39.

[9] Musavi M T，Ahmed W，Chan K H，et al.On the training of radial basis function classifiers[J].Neural Networks， 1992，5(4):595 ～ 603.

[10] Binchini M，Frasconi P，Gori M.Learning without local minima in radial basis function networks[J].IEEE Trans.on Neural Networks， 1995，6(3):749～755.

[11] 王雪萍，林康红.一种利用RBF神经网络的传感器建模新方法[J].新疆大学学报，2002，19(3):368～371.

[12] 徐丽娜.神经网络控制[M].哈尔滨:哈尔滨工业大学出版社，1999.

[13] 徐文，王大忠，周泽存，等.结合遗传算法的人工神经网络在电力变压器故障诊断中的应用[J].中国电机工程学报，1997，17(2):109～112.

[14] 潘羽中，陈伟根，云玉新，杜 林，孙才新.基于遗传算法进化小波神经网络的电力变压器故障诊断[J].电力系统自动化，2007，31(13):88～92.

[15] 金晶，苏勇.一种改进的自适应遗传算法[J].计算机工程与应用[J]，2005，18(2):64～68.

[16] 黄席樾，刘菡萏，石为人.基于遗传算法的RBF神经网络设计[J].重庆大学学报，1998，21(2):62 ～68.

[17] 郑丕谔，马艳华.RBF神经网络的递阶遗传训练新方法[J].控制与决策，2000，15(2):166～168.