湿空气凝结对ONERA M6机翼气动特性影响的数值研究

孙秀玲 ,李 亮 ,李国君

(西安交通大学能源与动力工程学院,陕西 西安 710049)

0 引 言

目前有许多求解Navier-Stokes方程对翼型绕流进行数值模拟的程序,它们对航空工业的发展起了巨大的推动作用。这些计算程序基本上都假设流动工质为完全气体,流动过程中不发生相变。然而在实际的大气飞行中,各种气象条件下空气中总是包含一定数量的水蒸汽,机翼周围压力、温度的变化在一定条件下会引起水蒸汽发生非平衡凝结现象。非平衡凝结是指水蒸汽膨胀越过饱和线后并不立即凝结,而是在热力学状态参数达到一定非平衡程度时才突然发生的凝结现象。图1显示了Tornado战斗机机翼表面附近凝结形成的水雾[1]。

大气飞行条件下1kg空气中平均的水蒸汽含量约为0.01kg,凝结放热量Q与CpT∞(Cp为来流空气比热,T∞为来流空气温度)的比值约为10%,这个量值的热量加入到跨声速气流中,不仅会显著改变机翼表面附近的压力、温度和超音速区大小等流动参数,甚至还会引起稳定或振荡的激波,从而导致机翼升力/阻力特性的显著改变[2-5]。

另一方面,凝结放热导致的激波与边界层相互作用,引起边界层位移厚度与动量厚度的显著增加,是诱发流动分离的原因之一[6],对机翼表面附近涡的产生和发展产生影响。此外,在飞机机动过程中,攻角、偏航角等参数的变化影响凝结过程,凝结过程反过来又会对机翼气动性能产生影响。这些因素综合作用,使得湿空气凝结现象对飞机在各种飞行姿态下的机动性能产生不可忽视的影响。此外,大气飞行中机翼等部位的结冰问题也与湿空气凝结现象紧密相关,湿空气凝结是形成冰晶的重要机制之一[7]。

图1 Tornado飞机机翼表面的凝结现象[1]Fig.1 Condensation around Tornado[1]

从上个世纪60年代起,不断有研究机构和学者对湿空气凝结流动问题开展研究。NASA在其8英尺风洞中研究了湿空气凝结对机翼气动性能的影响[8];Schnerr对NACA0012翼型和某圆弧翼型进行了一系列研究[3,5,6];Zierep[9],Rusak[10]等学者从凝结起始马赫数和凝结放热量等方面对凝结流动之间的相似性进行了理论分析,取得了一些进展。这些研究表明:跨声速流动与凝结过程相耦合,凝结过程与来流马赫数、攻角、空气湿度等参数之间存在强烈依赖关系,湿空气凝结对翼型升力/阻力特性有显著影响。尽管如此,在湿空气凝结流动研究方面,仍有一些重要的问题没有解决,目前尚没有一般性的结论指出在什么样的条件下(大气温度、压力、相对湿度、飞行速度、攻角、飞机几何特征参数等)发生凝结;另外,凝结影响机翼气动性能的一般规律也并不清楚。解决这些问题,对提高飞机在复杂大气条件和各种飞行姿态下的气动性能具有重要意义。

本文发展了湿空气非平衡凝结流动数学物理模型和计算方法,并对ONERA M6机翼周围的湿空气凝结流动进行了分析。

1 湿空气凝结流动数学物理模型

将湿空气凝结流视为一个两相系统:气相由干空气和水蒸汽即湿空气构成,凝结相为弥散在湿空气中所有凝结物的集合。在大气飞行条件下,由于水蒸汽相变发生的温度低于三相点温度,水蒸汽在跨声速条件下非平衡相变的产物可能是液态微小水滴或固态冰晶。相变过程影响机翼气动特性的本质是相变潜热对气流加热产生的影响。文献[11]指出,为了计算这种影响,可以假设相变产物为液态水,并在成核模型中对平面水的表面张力进行适当修正来计算成核过程中微小水滴的表面张力。因此本文假设湿空气相变产物为微小水滴。

由于跨声速湿空气流动中非平衡凝结形成的水滴直径在1μm以下,水滴和空气流之间的速度滑移可以忽略不计,因而可以建立如下欧拉/欧拉型的数值模型。描述气相即湿空气流动的质量、动量及能量守恒方程为

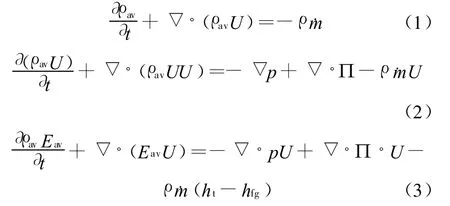
其中,ρav为湿空气密度,ρ为湿空气与水滴混合物的密度,U为速度矢量,П为应力张量,pav为湿空气静压,Eav为湿空气总能,ht为湿空气总焓,hfg为凝结潜热。引入源项-ρ﹒m、-ρ﹒mU、-ρ﹒m(ht-hfg)考虑流动过程中气液两相之间的相互作用对湿空气流动的影响,这里﹒m为质量凝结速率,其表达式为:

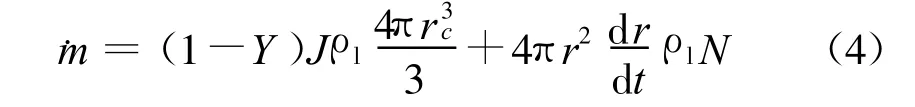
其中N为水滴数目,r为水滴半径,Y为凝结出的液态水在湿空气与水滴混合物中的质量百分数,J为成核率,dr/dt为水滴生长率,ρl为液态水密度,rc为临界半径。表达式(4)中两项分别考虑了成核和水滴生长对质量凝结速率的贡献。在求得液态水质量百分数和水滴数后,水滴半径由下式确定

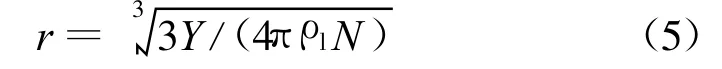
为了使方程组封闭,补充湿空气的状态方程

如前所述,由于假设凝结出的水滴与气相之间无速度滑移,因此对凝结出的液相只需描述水滴数目N和液态水质量份额Y。凝结形成的水滴实际上是具有不同半径的水滴族,如果对这些水滴族一一计算,会导致计算过程极其复杂。依据两相流理论,凝结形成的水滴遵循统计规律[13],因而可以采用体积平均的水滴数N进行计算。

另外在湿空气流中,随着水蒸汽不断凝结为水滴,湿空气中的含湿量也在不断减少,水蒸汽的分压随之减小。为了计算水蒸汽的当地分压力pv,还需要知道湿空气中含湿量d的分布。令

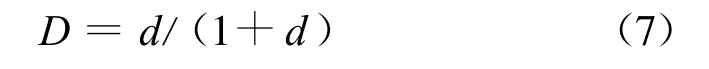
由含湿量定义可得ρv=ρavD,其中ρv为水蒸汽密度。由守恒定律可以得到描述N,Y及D分布的控制方程为

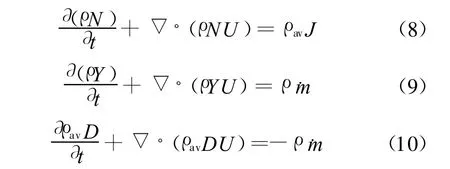
成核率J和水滴生长率dr/dt由经典成核理论计算,本文采用的表达式为[12]

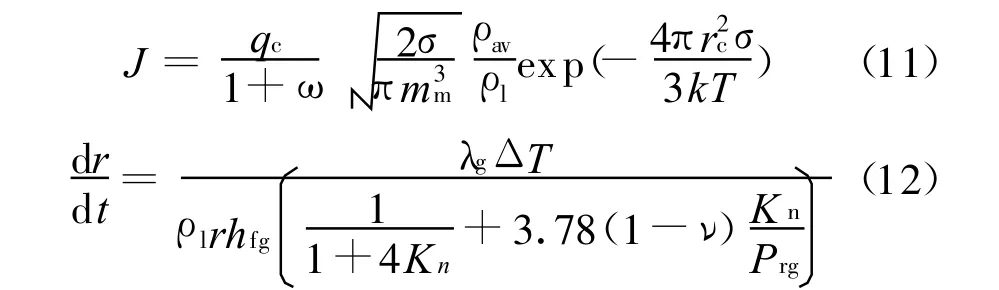
其中,ω和ν为两个修正系数,qc为凝结系数,σ为水滴表面张力,mm为水分子质量,k为热传导系数,T为温度,Kn为玻尔兹曼常数,Prg为普朗特数,过冷度ΔT由水蒸汽的当地分压力pv和温度T确定。

其中Ts为水蒸汽当地压力 pv对应的饱和温度。这样,由方程(1-3),方程(5、6)以及方程(8-10)就构成了求解跨声速湿空气非平衡凝结流动的全部方程。

需要说明的是,Schnerr[11]对湿空气凝结流动建立的模型中采用了面积平均的水滴半径,相应需要求解四个偏微分方程来描述水滴的大小和数目的分布。本文采用体积平均的水滴数N水滴半径r,由此由方程(8、9)即可确定水滴的分布,从而减少了计算量。由两相流理论[13],水滴的分布满足一定的统计规律,因此采用面积平均或体积平均的水滴半径本质上是相同的,计算结果一致,这一点由本文第3节的对比也可看到。

2 湿空气凝结流动数值计算方法

在湿空气两相非平衡凝结流动计算中,气液两相间的耦合方式及解法也是一个重要问题。二维气液两相流动的控制方程组联立求解时由于方程组的雅可比系数矩阵刚性较大,不易收敛,对三维流动,这个问题更加突出。本文处理方法是液相和气相各自作为相对独立的开口系,依靠在控制方程中添加考虑两相间相互作用的源项实现耦合计算。两相耦合关系如图2所示。气相即湿空气流动求解模块向液相求解模块传递湿空气密度ρav、压力pav、温度T及速度矢量U,液相模块由凝结模型(11、12)计算水滴成核率和生长率,并求解方程(8-10),由此得到液相凝结及水滴的分布情况;同时,液相模块向气相流动求解模块传递质量凝结速率﹒m和凝结潜热hfg,从而可以计算方程(1-3)中的源项。采用这种方式,可以在大量已有的单相流动计算程序基础上发展湿空气凝结流动的计算程序。

图2 两相耦合方式Fig.2 Interphase coupling

在机翼的湿空气非平衡凝结绕流计算中,一方面机翼表面附近可能存在气动激波,另一方面,由于非平衡凝结发生的突然性,凝结流场中液相参数变化剧烈,而且凝结过程对当地流动参数的变化很敏感。因此,在数值求解中需要采用高分辨率的差分格式。在本文计算中,对气液两相方程组的求解均采用了Harten提出的TVD格式[14]。

这样气相方程(1-3)和液相方程(8、9、14)均可在直角坐标系下分别写为如下矢量形式

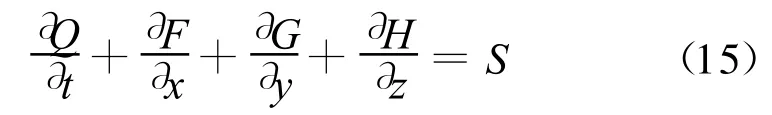
对于NS方程计算,紊流模型采用SA模型,可以与气相方程(1-3)统一写成式(15)的形式。直角坐标系下三个方向的离散方法相同。以方向为例,令A=∂F/∂Q=RΛ R-1,其中 R 为A 的特征矩阵,R-1为R的逆阵,Λ为A的特征值构成的对角阵。方程(15)离散为,

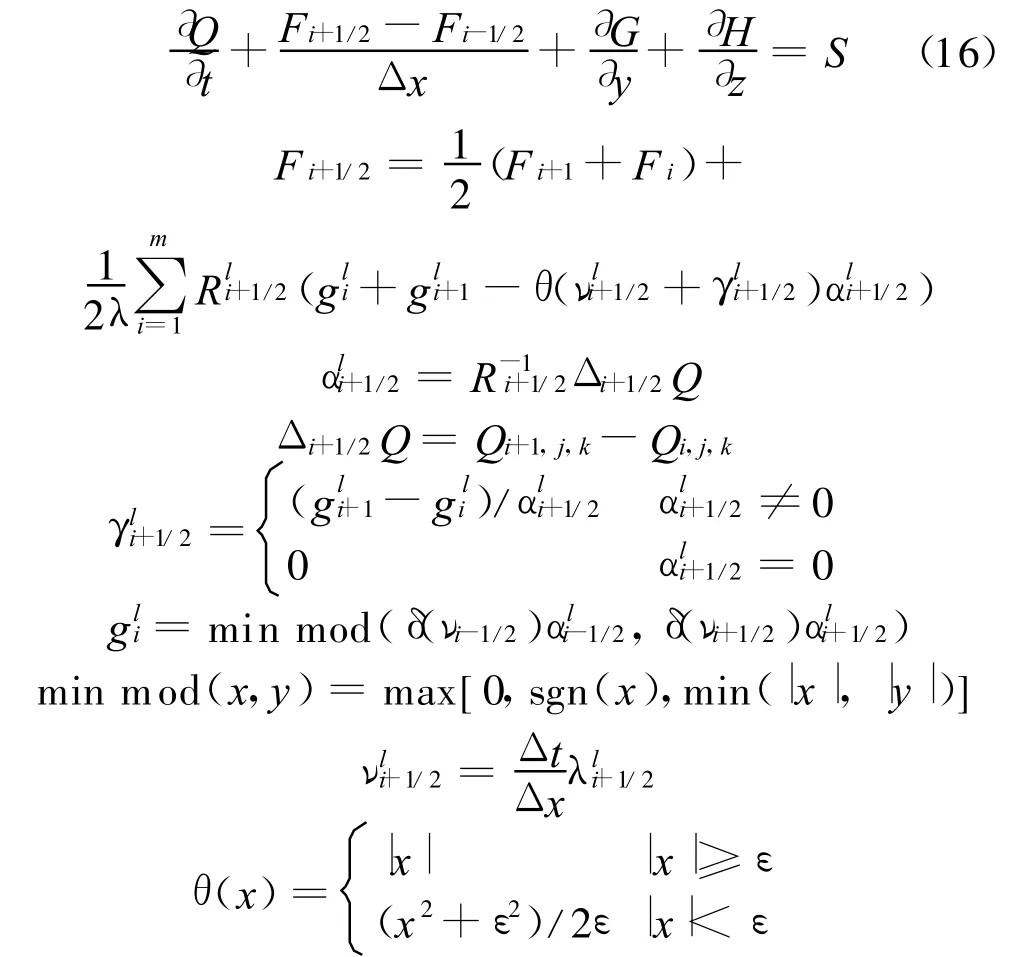
求解中采用显式时间推进,紊流模型采用SA模型。气相方程组求解时,远场边界给定湿空气的压力、温度、相对湿度或含湿量,翼面给定粘性固体边界。液相方程求解中,远场及翼面边界条件均由内点外推。求解中为了保证计算稳定,湿空气流动计算的CFL数取为干空气流动计算时的0.1倍。

3 湿空气凝结流动模型验证

首先对NACA0012翼型周围的湿空气凝结流动进行了无粘计算。由于缺乏湿空气凝结流动中翼型表面压力系数的试验数据,因此计算结果与文献[11]中的结果进行了比较,以验证本文所建立的模型。计算中的流动条件为:弦长c=0.1m,压力p∞=65600Pa,温度 T∞=259K,马赫数 M∞=0.8,相对湿度 φ∞=50%,攻角 α=0°。远场边界距翼型约30倍弦长。

计算得到的翼型表面压力系数分布如图3所示。可以看到,本文结果与文献[11]中的结果吻合良好。在相对湿度φ∞=50%的流动中,由于水蒸汽凝结放热对气流加热,激波前马赫数明显减小,激波位置也向上游移动,导致翼型表面压力系数发生显著变化。

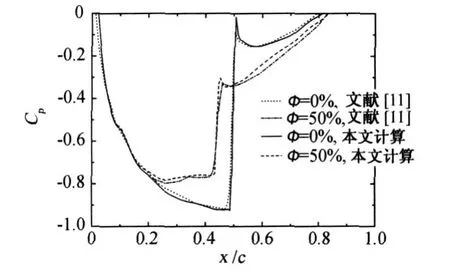
图3 NACA0012翼型表面压力系数分布Fig.3 Pressure coefficient of NACA0012 airfoil

4 机翼湿空气凝结流动分析

利用本文发展的数值方法对ONERA M6机翼[15]周围的湿空气凝结流动进行了分析。计算中流动条件为压力 p∞=129000Pa,温度 T∞=293.15K,马赫数Ma∞ =0.84,攻角 α=3.06°,相对湿度 φ∞ =50%,计算网格总数约为30万。

沿ONERA M6机翼展向三个截面的压力系数如图4所示。干空气(φ∞=0%)流动计算清晰地捕获到了机翼表面的激波;而在湿空气(φ∞=50%)流动中,由于凝结潜热对跨声速气流的加热作用,导致激波消失。另外,与干空气(φ∞=0%)流动相比,湿空气(φ∞=50%)凝结流动中机翼下表面压力系数变化不大,而上表面压力系数则有显著变化。这是由于下表面气流膨胀速率低,凝结过程不明显,凝结放热对流动的影响较小;而上表面的跨声速流动中,由于发生明显的湿空气凝结放热,对跨声速流动造成了显著影响,从而使机翼上表面的压力系数发生明显变化。这一点也可以从下文图7机翼表面附近凝结出的液态水质量份额看到。

为了分析凝结放热对气流参数的影响,图5给出干空气流动和湿空气凝结流动条件下机翼表面附近的马赫数分布。可以看到,凝结流动中机翼上表面激波前的马赫数减小,并且沿着翼展方向减小的幅度越来越大,这与图4中两种流动条件下压力系数的变化相对应。

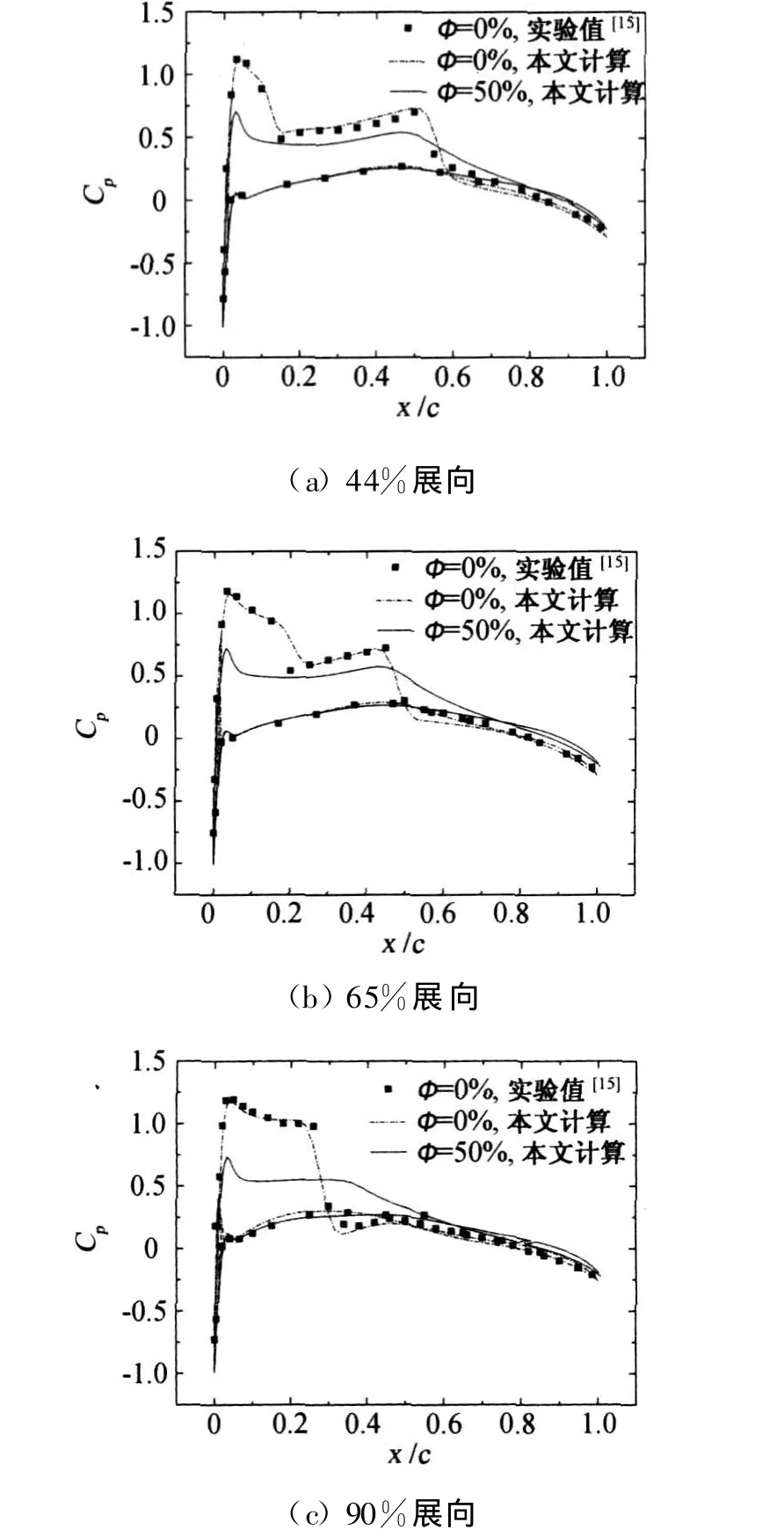
图4 ONERA M6机翼表面压力系数分布Fig.4 Pressure coefficient of ONERA M6 wing

图6给出ONERA M6机翼上表面压力等值线分布。可以看到干空气流动中上表面附近形成了清晰的λ形激波;而在湿空气凝结流动中,由于凝结放热使马赫数减小,λ形激波结构消失,激波位置向下游移动,并且激波强度也明显减弱。

机翼表面压力系数的变化是由于空气中水蒸汽凝结,相变潜热对跨声速气流加热,导致机翼表面附近流动参数发生改变的结果。因此机翼气动特性的改变与机翼表面附近的凝结过程直接相关。图7给出了65%翼展位置机翼表面附近凝结出的液态水的质量份额Y,沿翼展其它位置处Y的分布与此类似。在机翼上表面,由于凝结发生在前缘,整个上表面附近的液态水质量份额约为1%;下表面凝结发生的位置向后移动,在50%弦长以后才可以凝结,机翼下表面附近的液态水质量份额约为0.5%。

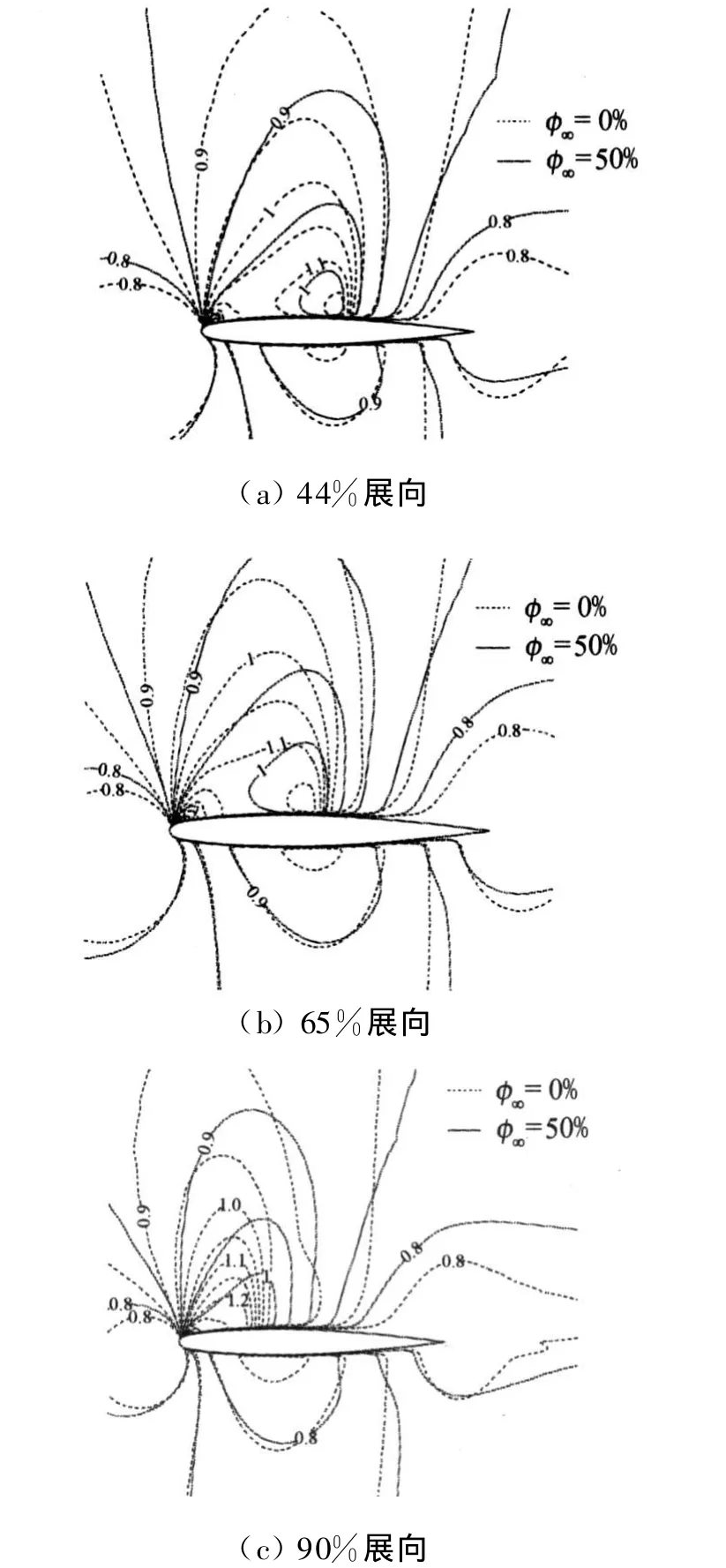
图5 ONERA M6机翼表面附近马赫数等值线分布(等值线间隔0.05)Fig.5 Contours of Mach number of ONERAM6 wing(ΔM=0.05)

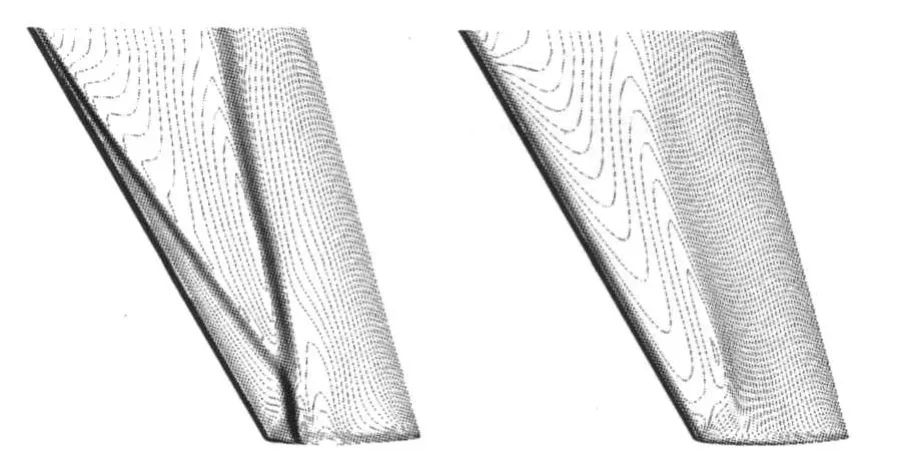
图6 ONERA M6机翼上表面压力等值线分布Fig.6 Upper surface pressure of ONERA M6 wing

图7 65%展向位置处ONERA M6表面附近液态水质量份额Y(Δ Y=0.002)Fig.7 Mass fraction of waterY around ONERA M6 wing at 65%span(Δ Y=0.002)

5 结论与展望

湿空气中的水蒸汽凝结对机翼气动特性会造成显著影响。本文建立了湿空气非平衡凝结流动的数值模型,并对ONERA M6机翼进行了湿空气非平衡凝结流动的初步研究。在攻角为3.06°和空气相对湿度50%时的ONERA M6机翼湿空气凝结流动与干空气流动相比,机翼表面压力系数有显著变化。造成机翼气动特性显著变化的原因在于:湿空气中水蒸汽凝结放热对跨声速气流加热,导致机翼表面附近的流速、压力与流场结构发生了显著变化。

湿空气凝结流动研究涉及复杂的相变过程,如果考虑大气中尘埃、离子等各种微小悬浮颗粒对凝结过程的影响,模型将更为复杂。但湿空气凝结对机翼气动特性的影响显著,有必要在试验和计算方面进一步开展深入的研究工作。

[1]http://www.steehouwer.com[DB/OL].

[2]CAM PBELL J F,CHAMBERS J R,AND RUMSEY C L.Oberservation of airplane flow fields by natural condensation effects[J].J.Aircraft,1989,26(7):593-604.

[3]SCHNERR G H,MUNDINGER G.Similarity,drag and lift in transonic flow with given internal heat addition[J].Eur.J.Mech.,B/Fluids,1993,12(5):597-612.

[4]LI L,SUN X,FENG Z and LI G.Transonic flow of moist air around a NACA 0012 airfoil with non-equilibrium condensa-tion[J].Progress in Natural Science,2005,15(9):838-842.

[5]SCHNERR G H.Transonic aerodynamics including strong effects from heat addition[J].ComputersFluids,1993,22(2-3):103-116.

[6]SCHNERR G H,LI P.Shock wave/boundary layer interaction with heat addition by non-equilibrium phase transition[J].Int.J.Multiphase Flow,1993,19(5):737-749.

[7]WILLIAM L W,GLENN G,THOMAS J H,et al.AircRAFT-PRODUCED ICE PArticles(APIPs):additional results and further insights[J].J.Applied Meteorology,2003,42(5):640-652.

[8]JORDAN F L.Investigation at near-sonic speed of some effects ofhumidity on the longitudinal aerodynamic characteris-tics of a NASA supercritical wing research airplane model[R].NASA-TM-X-2618,1972.

[9]ZIEREP J,LIN S.Bestimmung des kondensation-beginns bei der entspannung ǜfeuchter luft in berschalldǜsen[J].For-schung im Ingenieurwesen,1967,33(6):169-172.

[10]RUSAK Z,LEE J C.Transonic flow of moist air around a thin airfoil with non-equilibrium and homogeneous condensa-tion[J].J.Fluid Mechanics,2000,43(1):173-199.

[11]SCHNERR G H,DOHRMANN U.Transonic flow around airfoils with relaxation and energy supply by homogeneous condensation[J].AIAA Journal,1990,28(7):1187-1193.

[12]GUHA A.,YOUNG J.B.Time-marching prediction of unsteady condensation phenomena due to supercritical heat addi-tion[J].IMechE,1991,C423/057.

[13]MOORE M J,SIEVERDING C H.Two-phase steam flow in turbines and separators[M].Hemisphere Publishing Corpora-tion,1976.

[14]HARTEN A.High resolution schemes for hypersonic conservation laws[J].Journalof Computational Physics,1983,49:357-393.

[15]http://www.grc.nasa.gov/WWW/wind/valid/archive.html[DB/OL].