高速公路场景中车用自组织网络的节点度

熊 炜 李清泉

①(武汉大学电子信息学院 武汉 430079)②(武汉大学交通研究中心 武汉 430079)

③(武汉大学测绘遥感信息工程国家重点实验室 武汉 430079)

1 引言

随着交通祸害的日益严重，交通治理观念的转变，政府交通政策的改变以及运用智能交通(ITS)改善道路运输状况的成效等诸多方面的因素，使得研究与发展ITS已经成为当前科技竞争的前沿热点领域之一。车用自组织网络(VANET)作为ITS的一个重要组成部分，近年来也一直备受交通发达国家的广泛关注，它是移动自组织网络(MANET)与无线传感器网络(WSN)在ITS中的具体应用。借助车辆与车辆(V2V)、车辆与路旁基础设施(V2I)以及车辆与行人(V2P)之间的直接或多跳通信，从而在现有道路网上动态、快速构建一个自组织、分布式控制的专用短程通信(DSRC)网络成为现实。通过运用新兴的车-X通信技术，可以实现诸如道路安全告警、交通拥塞监测以及基于位置的流媒体服务等方面的应用[1]。由于VANET独具的特点(例如车辆运动的高速性、频繁的网络分裂、网络易受驾驶员行为等因素的影响[2])，针对MANET/WSN所做的研究成果并不能够直接应用于新兴的VANET系统。

目前，VANET研究人员在车用媒介访问控制(MAC)、数据分发、通信安全以及运动建模等方面取得了较好的研究进展[3,4]，但对于车辆网络能够提供可靠服务的先决条件，即VANET拓扑连通性方面的研究还相对较少。文献[5]探讨了影响车辆间通信网络连通性的诸多关键因素，例如车流密度、相对速度、车道数等。文献[6]利用元胞自动机模拟信息的传播过程，给出了相距为d的两车之间在不同交通环境以及不同通信距离下通过IVC建立连接的概率。文献[7]分析得出了无线通信范围r内至少存在一个VANET节点的概率。文献[8]通过研究紧急告警信息在双向多车道高速公路场景中的传播机制，得出了在被影响区域L内可将紧急告警消息转发给至少一个其它有效车辆的概率。文献[9]运用复杂网络的传播机理，研究了VANET市场普及率(即具有车载无线通信设备的车辆占道路中所有行驶车辆的比率)对交通信息的传播效率及传播速度的影响，并从消息纵向传播的动力学分析中得出转发概率有赖于节点最大通信距离的结论。文献[10]提出了一个分析模型用以计算沿交通流方向覆盖每一辆车的概率，该递归模型为瞬时传输距离的建模提供了一种数值计算的方法；随后文献[11]在此基础上，分析了VANET节点密度、节点通信距离以及信息传播距离之间的关系，并给出了计算信息传播距离的数学期望、方差及其概率分布的闭合解析式。文献[12]基于公认的交通流分布，通过引入摄动机制模拟驾驶员行为，研究了单向有限长度高速公路场景中VANET连通性问题，并给出了网络高概率连通所需的节点邻居数下限。文献[13]则推导得出了双向4车道场景中无孤立节点的存在概率。

纵观国内外的研究现状，研究重点主要集中在非孤立节点方面，即节点通信范围内至少存在一个邻居车辆的概率，但对车辆节点之间存在冗余链路方面的研究还尚未引起足够重视。为此，本文在已有研究的基础上，重点考查车辆网络的k-邻居问题，并推导得出一种用于高速公路场景中车用自组织网络节点度的概率计算方法。文献[14]与本文的研究较为接近，然而前者在分析得出MANET的最小节点度时，并未考虑车辆网络的约束性。本文属于网络k-连通性范畴，在文献[13]提出的算法基础上，对VANET的冗余节点度(即k=1,2,3,…)做了进一步深入研究，因此从某种意义上而言，文献[13]是本文在k=1时的特例。本文在以下几个方面取得了较好的研究进展：(1)高速公路场景中车辆运动建模；(2)高速公路场景中无线信道建模；(3)VANET随节点通信距离的变化表现出的特殊性；(4)VANET中节点度至少为k的概率计算公式。

2 VANET系统建模

2.1 车辆运动模型

对自组织网络的研究表明，协议性能的优劣在很大程度上取决于所选择的节点运动模型，并且MANET研究中经常采用的随机路点(RWP)和随机方向(RD)运动模型不适合模拟车辆的运动，另外，通过大规模现场实验以期获得一定数量、真实的车辆轨迹数据代价太大，因此，微观交通仿真系统可用于生成研究所需的车辆运动。本文使用的车辆运动轨迹数据来源于HWGui项目[15]，原始车辆运动数据由DaimlerChrysler内部的驾驶员行为模拟器产生，并同高速公路上采集到的真实车辆运动数据进行了比较。它对交通流的描述是以单个车辆为基本单元，车辆在道路上的跟车、超车以及车道变换等微观行为都能够得到真实的反映。

运动数据的格式为每个车辆节点(NodeID)在采样时刻(Timestep)具有的瞬时位置(PositionX)、速度(Speed)、加速度(Acceleration)及车道(Lane)信息，转换成NS-2兼容的TCL运动格式后，相当于车辆在如图1所示的双向4车道高速公路模型中连续运动。不同密度的车流可沿着被中间带分隔且与车道平行的两个方向(如图中箭头所示)高速运动，每个方向再具体划分为行车道(行进方向右手侧)和超车道(行进方向左手侧)。本文规定：行/超车道宽度LaneWidth=3.75 m，中央分隔带宽度MedianWidth=2.00 m。

由于每个车辆节点在高速公路上的坐标位置均由2元组(PositionX, Lane)表示，因此在模拟实验中，车辆的车道变换过程总是在相邻两次采样间隔(0.5 s)内完成。为了简化数据处理，我们用车辆所在车道的中线表示其在Y方向上的投影(PositionY)，若采用图1中所示的坐标系统，则映射关系式为

图1 高速公路场景模型

2.2 无线传播模型

信号通过无线信道时，会遭受各种衰落的影响，可以分为[16]：大尺度衰落和小尺度衰落。其中大尺度衰落是由于传播距离的路径损耗或传播环境(例如地形起伏、高大建筑等障碍物)的遮挡所致，它通常与射频频率无关。小尺度衰落则是由于无线电波在空间传播时存在反射、绕射和衍射等机制，从而造成信号经由多条路径到达接收端叠加形成，与所选信号频率有关。

复杂的统计模型(例如瑞利、莱斯、Nakagami等分布)可以用来描述无线传播的多径衰落，但对无线链路性能及无线通信方式的研究表明[17,18]：基于几何光学的双线模型(同时考虑视距直接传播与地面反射路径)在预测高速公路场景中的专用短距离通信时也具有良好的效果。本文采用式(2)所示的广义对数距离路径损耗模型为无线信道建模：

其中Prx/Ptx分别为收/发信号功率，d为收发之间的距离，d0为近地参考距离(由测试决定)，β为路径损耗指数，它表明路径损耗随距离增长的速率，在视距以及非视距车辆通信场景中分别为1.4～3.5和2.8～5.9[19]。因此，在给定接收灵敏度Prx,th时，每个节点的无线通信距离可以由其等效发送功率来计算。当Prx(d)＜Prx,th时，我们就认为两节点之间不存在无线通信链路。本文假定场景中所有车辆节点都相同，即具有相同的射频功率和接收灵敏度，并采用全方向天线。

3 k-近邻节点概率

基于前述的VANET系统模型，本文将高速公路场景中每个采样时刻t所对应的车辆网络表示为一个简单无向图Gp(r)(V, t)，其中，V表示实验场景中的所有活动车辆，其网络规模为N=|V|，p(r)则表示当节点通信距离为r时，场景中任意两个节点之间边(即无线通信链路)的存在概率。如果记符号||⋅||为实d-维向量空间ℝd上的范数，对于给定分布的有限点集V⊂ℝd，当且仅当||vj-vi||≤r时，两节点{vi,vj}互为邻居。不防设离散型随机变量D为图中任意节点v∈V的可能顶点度。以下将从交通工程学的角度出发，推导网络或图中节点度至少为k的概率Pr{D≥k}。

在交通流理论中，车头间距(hs)与车头时距(ht)是两个非常重要的微观交通特征参数，它们是表征同一概念的两种不同量度单位，分别用来描述在同向行驶的车流中，前后相邻两车之间的空间距离以及驶过道路某一断面的时间间隔，其取值与驾驶员行为特征、车辆性能、道路具体情况密切相关，同时也受到交通流量、交通控制方式以及道路几何特征等因素的影响。实际工程应用中，由于车头间距的实时测量非常困难，一般仅使用车头时距这个指标。在自由流(例如高速公路上的交通流)条件下，其车头时距服从指数分布[7,9,12]，并且可以证明，车辆到达数在任意计时周期内一定是泊松分布。如果车流速度vs同时满足均匀分布，则车头间距与车头时距具有完全相同的指数分布形式[7,12](hs=vsht)。由于车流密度被定义为κ=N/(Lm)，其中，N为车辆数，m为车道数，L为观测路段的长度。于是，在车辆节点通信范围A内至少存在k个邻居的概率为

其中λ=1/(vs⋅ht⋅m⋅LaneWidth)是一个与高速公路模型、车头时距、车辆运动速度有关的物理量。由于车辆网络固有的技术特点，对组网真正产生贡献的有效作用面积为带状行车区域和无线覆盖范围的交集。关于有效组网面积的详细讨论，读者可以参见文献[13]，考虑到篇幅限制，本文仅对节点通信距离足够大(即r＞3.5×LaneWidth+MedianWidth)的情况进行分析。

若记A1，A2为带状行车区域分别与行车道(i=1)、超车道(i=2)上车辆节点的无线覆盖范围所形成的公共面积(如图1所示)，于是有

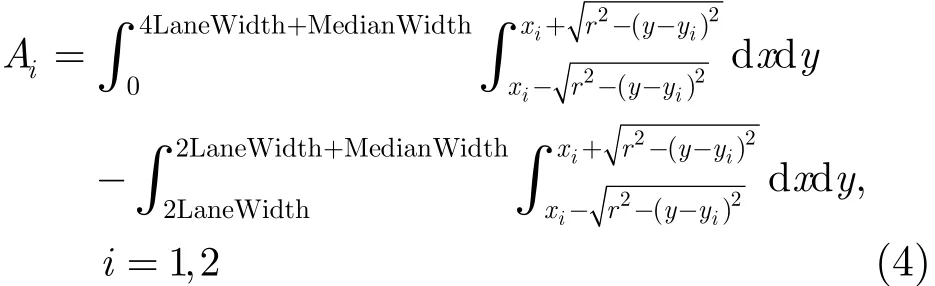
式(4)中的两个二重积分非常相似，差异主要在于积分变量y的上/下限不同，因此只需要计算以下二重积分即可。

令y−yi=rsin(t)，则有=rcos(t)，dy=rcos(t)dt ，t=arcsin(y−yi)/r ，将它们代入式(5)得

(2)在嵌入的双对数坐标系中，当节点通信距离较大时，其与车道平均系数之间具有幂律特征(对应为一条直线)，即c～r−γ，本文仅对100～1000 m处的车道平均系数做最小二乘拟合得γ=0.9988，此时对应的残差平方和仅为1.0575×10−6。

图2 行车道与超车道系数

4 实验与分析

本文使用的车辆运动轨迹数据来源于HWGui项目，采用地面反射双线模型为无线信道建模(通信频率设为5.9 GHz DSRC专用频段，无线模型的其它参数采用NS-2中的默认值)。为了验证推导得出的理论分析结果与实际的车辆网络模型之间的匹配效果，作者选取5组不同车流密度下的车辆运动轨迹数据进行实验，表1列出了实验场景中车辆网络的部分运动数字特征。

图3为场景1中节点度至少为1的实验概率曲线分别与相同参数的3条理论概率曲线之间的比较，其中，虚线是将高速公路视为1维(线性)场景时的理论概率，点划线是将高速公路视为2维(带状)场景且有效组网区域视为圆时的理论概率，实线则是将高速公路视为2维(带状)场景且有效组网区域为本文提出的弧边矩形时的理论概率。从图中可以看出，可以将高速公路场景中的车用自组织网络视为1维线性或2维带状，但是在2维带状条件下，节点间的有效组网区域必须限制为弧边矩形，即理论分析中须除去节点不可达的部分。此外，相对于虚线而言，实线更逼近于实际实验曲线，并且当节点通信距离较小时，实线以点划线作为其渐近线；当节点通信距离较大时，实线又以虚线作为其渐近线。换言之，在节点通信距离较小时，高速公路场景中的车用自组织网络具有较为明显的2维特性；但在节点通信距离较大时，其又转而具有明显的1维特性，这也进一步说明了VANET的特殊性。对于其它实验场景在不同节点度时也都有类似的结论。

表1 实验场景中车辆网络的运动数字特征

图3 理论概率与实验概率对比

图4，图5和图6分别为VANET场景中节点近邻数至少为1，2和3的概率。其中，图4(a)，5(a)，6(a)的3维网格图是在给定场景(其长度L=12000 m)中的理论概率及其对应的等高线投影，网格图中任意两曲线的交点即为在给定(N, r)条件下，节点度至少为k的概率；图4(b)，5(b)，6(b)分别为5组不同车流密度下的节点度实验概率与本文推导得出的k-近邻节点概率(相同参数下的理论概率)之间的比较，可以看出，在所有这5组实验场景中，节点度的理论概率与实验概率吻合得较好，并且当场景中节点数N以及节点通信距离r一定时，随着节点邻居数k的增加，其存在概率越小。例如若N=50，r=250 m，网络中所需节点度至少等于1，2和3的理论概率分别为0.8754，0.6158和0.3456。此外，若给定网络所需的最小节点度，则：(1)在相同通信距离的条件下，随着车流密度的增加，Pr{D≥k}越大；(2)在相同Pr{D≥k}的条件下，场景中车流密度越大，所需的节点通信距离越小。这与有关文献所得的结论完全一致。

5 结束语

本文基于地面反射双线模型将车辆网络建模为(路径损耗)几何随机图，并在已有研究的基础上向前迈进了一步，重点研究了高速公路场景中车用自组织网络的k-邻居问题，推导得出了计算VANET节点度至少为k的概率分析算法，并借助真实的车辆运动轨迹数据做了大量模拟实验。本文的主要贡献在于：(1)将VANET建模为几何随机图，并提出了弧边矩形有效组网面积的概念，即高速公路带状行车区域与无线信号覆盖范围的交集，并将其由2维场景中的πr2紧缩为cr2，其中c＜π；(2)分析说明了车辆间通信网络所具有的特殊性，即随着节点通信距离的增加，其网络属性将逐渐由2维模式过渡到1维模式，并最终以1维模型对应的概率曲线作为其渐近线(相对于1维模型而言，本文推导得出的理论概率更逼近实验概率)；(3)推导得出了无线通信范围内至少存在k≥1个VANET邻居的概率，根据式(8)可以解算出，场景中所需的网络规模N、节点通信距离r以及网络中节点度至少为k的概率Pr{D≥k}三者之间的数值关系。

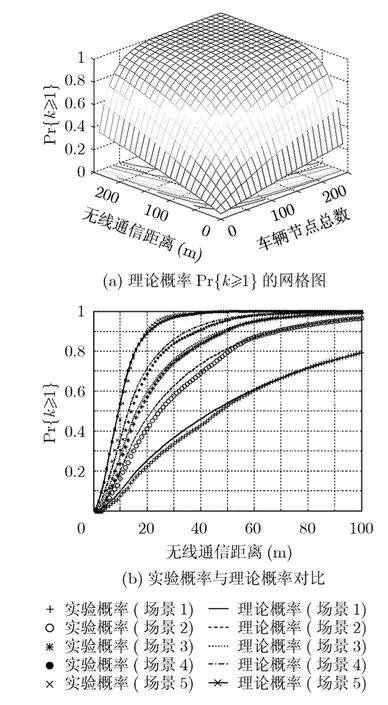
图4 场景中节点度至少为1的概率

图5 场景中节点度至少为2的概率

图6 场景中节点度至少为3的概率

对于车用自组织网络连通性方面还存在一些问题有待于作者做进一步的分析与研究，例如：VANET在高速公路场景中节点度与网络连通性之间的关系以及VANET在市区内的连通性分析等。

[1] Hartenstein H and Laberteaux K P. A tutorial survey on vehicular Ad hoc networks. IEEE Communications Magazine,2008, 46(6): 164-171.

[2] Toor Y, Muhlethaler P, and Laouiti A, et al.. Vehicle Ad hoc networks: applications and related technical issues. IEEE Communications Surveys & Tutorials, 2008, 10(3): 74-88.

[3] Moustafa H and Zhang Y. Vehicular networks: techniques,standards, and applications. NW: Auerbach Publishers, CRC Press, Taylor & Francis Group, 2009.

[4] Olariu S and Weigle M C. Vehicular networks: from theory to practice. NW: Chapman & Hall, CRC Press, Taylor &Francis Group, 2009.

[5] Artimy M M, Robertson W, and Phillips W J. Connectivity in inter-vehicle ad hoc networks. Proceedings of Canadian Conference on Electrical and Computer Engineering, Niagara Falls, Canada, 2004, Vol. 1: 293-298.

[6] Hartenstein H, Bochow B, and Ebner A, et al.. Position-aware ad hoc wireless networks for inter-vehicle communications:the fleetnet project. Proceedings of the 2nd ACM International Symposium on Mobile Ad hoc Networking &Computing, Long Beach, CA, USA, 2001: 259-262.

[7] Tsugawa S and Kato S. Evaluation of incident information transmission on highways over inter-vehicle communications.Proceedings of the IEEE Intelligent Vehicles Symposium(IV-2003), Columbus, Ohio, USA, 2003: 12-16.

[8] Tondl P and Pérez Guirao M D. Forwarding of emergency notifications in one-dimensional networks. Inter-vehiclecommunications based on Ad hoc Networking Principles - the FleetNet Project. Karlsruhe, Germany, Universitätsverlag Karlsruhe, 2005: 83-116.

[9] Schönhof M, Kesting A, and Treiber M, et al.. Coupled vehicle and information flows: message transport on a dynamic vehicle network. Physica A: Statistical Mechanics and its Applications, 2006, 363(1): 73-81.

[10] Jin W-L and Recker W W. Instantaneous information propagation in a traffic stream through inter-vehicle communication. Transportation Research Part B:Methodological, 2006, 40(3): 230-250.

[11] Wang X. Modeling the process of information relay through inter-vehicle communication. Transportation Research Part B:Methodological, 2007, 41(6): 684-700.

[12] Ukkusuri S and Du L. Geometric connectivity of vehicular Ad hoc networks: analytical characterization. Transportations on Research Part C: Emerging Technologies, 2008, 16(5):615-634.

[13] 熊炜, 李清泉. 高速公路场景中车用自组织网络1-连通的必要条件. 软件学报, 2009. Available: http://www.jos.org.cn/1000-9825/3681.htm.Xiong W and Li Q Q. Prerequisite to 1-connected vehicular Ad hoc networks in highway scenarios. Journal of Software,2009. Available: http://www.jos.org.cn/ 1000-9825/3681.htm.

[14] Bettstetter C. On the minimum node degree and connectivity of a wireless multihop network. Proceedings of the 3rd ACM International Symposium on Mobile Ad hoc Networking &Computing, Lausanne, Switzerland, 2002: 80-91.

[15] Füßler H, Torrent-Moreno M, and Transier M, et al..Studying vehicle movements on highways and their impact on ad-hoc connectivity. ACM SIGMOBILE Mobile Computing and Communications Review, 2006, 10(4): 26-27.

[16] Rappaport T S. Wireless Communications: Principles and Practice. 2nd ed. New Jersey: Prentice Hall PTR, 2002, Chap.4-5.

[17] Zang Y, Stibor L, and Orfanos G, et al.. An error model for inter-vehicle communications in highway scenarios at 5.9GHz.Proceedings of the 2nd ACM International Workshop on Performance Evaluation of Wireless Ad hoc, Sensor, and Ubiquitous Networks, Montreal, Quebec, Canada, 2005:49-56.

[18] Gallagher B, Akatsuka H, and Suzuki H. Wireless communications for vehicle safety: radio link performance and wireless connectivity methods. IEEE Vehicular Technology Magazine, 2006, 1(4): 4-24.

[19] Yin J, ElBatt T, and Yeung G, et al.. Performance evaluation of safety applications over DSRC vehicular ad hoc networks.Proceedings of the 1st ACM International Workshop on Vehicular Ad hoc Networks, Philadelphia, PA, USA, 2004:1-9.