分光光度法测定聚丙烯酸酯乳液的稳定性

吴广峰， 周宝库， 丛 滨， 陶 悦， 张凤东

（1.长春工业大学化学工程学院，吉林长春 130012; 2.中国石油管道长春输油气分公司，吉林长春 130011; 3.中国石油吉林天然气管道有限公司，吉林长春 130011; 4.长春理工大学理学院，吉林长春 130022）

0 引 言

聚丙烯酸酯乳液是丙烯酸酯类单体以水为分散介质，在乳化剂作用下，经乳液聚合而成的高分子水乳液，广泛应用于纺织、印染、造纸、涂料、胶粘和油田化学品等领域，也是制备塑料增韧剂[1]的方法之一。乳液产品在生产和使用过程中要保持稳定性才能保证产品的正常使用，所以研究聚丙烯酸酯乳液的稳定性有重要的意义。研究乳液体系稳定性常采用冻融法[2]、凝胶含量法[3-4]、机械法[5]等，但这些方法只能粗略地评价乳液的稳定性，不能给出定量数据。分光光度法[6]具有操作方便、精度高、应用范围广等优点，适合跟踪溶液中的悬浮粒子数量变化。

文中利用分光光度计的浊度法[7-8]对乳液的稳定性进行了定量的表征，得到了影响乳液稳定性的临界盐浓度的量化指标，以期为工业生产提供参考。

1 实验部分

1.1 试剂与仪器

丙烯酸丁酯（BA）、甲基丙烯酸甲酯（MMA），工业品，中油吉化股份有限公司;

甲基丙烯酸缩水甘油酯（GMA），工业品，苏州安利化工厂;

十二烷基硫酸钠（SDS），工业品，山西长治澳尼克合成化学公司;

过硫酸钾（KPS），工业品，广西西拢化工厂;

无水硫酸镁（MgSO4），分析纯，北京益利精细化学品有限公司;

实验用水为去离子水。

UV754N紫外可见分光光度计，上海精密科学仪器有限公司;

电热恒温水浴锅，北京华恒万仪仪器有限公司。

1.2 乳胶粒子的制备

在装有回流冷凝管、通氮气管、搅拌器的三口瓶中加入一定比例的SDS、蒸馏水，控制反应温度在60℃，氮气气氛，搅拌20 min后加入一定量的引发剂KPS和BA单体，合成聚丙烯酸丁酯（PBA）核乳液。再补加KPS，滴加MMA及不同比例的GMA混合物，滴完后继续恒温2 h，即得到所需的产物聚丙烯酸酯乳液产品，它是一种性能优异的塑料用抗冲击改性剂，也可以作为涂料和防水材料使用。

1.3 稳定性测试原理及方法

在室温条件下，乳液可以存放长达几年，是动力学稳定体系，但最终它还是会失去稳定性而变质。如果向乳状液中加入电解质，会加速其失稳的过程，使乳状液极快地变质，因此，乳液不是热力学稳定体系。

乳液失稳过程的理论被称为DLVO理论，是由Derjaguin和 Landau[9]以及Verwey和Overbeek[10]提出的。DLVO理论认为，两个乳胶粒子间相互作用的总势能VT是乳胶粒子间的范德华引力势能VA和乳胶粒子上的双电层因相互靠近而产生的静电斥力势能VR相加和的结果。若将极近距离的斥力能考虑进来，并将粒子间相互作用总势能VT对粒子表面间距离h作图，能够得到势能-距离曲线[11]。曲线中近距离处有一个极小值，它表示粒子间能够接近的最小距离;随着距离的增加，静电斥力势能VR以指数形式衰减，而范德华引力势能VA的绝对值以冥律形式衰减，两者加和的结果是使曲线又出现一个极小值Vsm。

理论上，将分散在连续相中的材料相同、半径a相同、表面电势ψs相同的球形粒子称作单分散体系，实际上通常将多分散指数（Polydispersity Index）小于1.0的体系看作是单分散体系。对于单分散体系中的两个粒子，Reerink和 Overbeek[12]给出了静电斥力势能VR的定量表达式:

对于同样的两个球形粒子，Hamaker[13]给出了范德华引力势能VA的定量表达式:

式中:x=h/2;

A——Hamaker参数;

A11——乳胶粒子的Hamaker常数;

A22——分散介质的Hamaker常数。

当x≪1时，有:

在乳液中引入电解质将压缩乳胶粒子周围双电层，也会使分散介质中的离子被吸附到Stern层，导致双电层的排斥力减小，结果使乳胶粒接近到使范德华力占优势的程度。这时，乳胶粒子的布朗运动会使乳胶粒碰撞后不可逆地粘在一起，直至粘连体受重力作用沉降出来，即所谓的聚沉现象。

Smoluchowski[14]提出了聚沉过程起始阶段的动力学模型，认为初始粒子的无能垒消失速率可由下式表达:

式中:N0——乳胶粒子的初始数浓度;

kf——与胶体粒子的扩散系数D有关的快速聚沉速率常数。

Fuchs和Overbeek[15]提出了有能垒存在时，聚沉起始阶段粒子的消失速率方程:

式中:W——稳定因子。

当没有能垒存在，即VT=0时，W=1，聚沉速率-dN/dt=kfN20;当有能垒存在，即VT＞0时，W＞1，聚沉速率-dN/dt=kN20，k为慢速聚沉的速率常数，这样，W就可由kf/k得出。以logW对电解质浓度的对数logC作图，能够得到一条直线，它与直线W=1的交点代表着乳状液由慢速聚沉向快速聚沉转变的最低电解质浓度，称为临界聚沉浓度 CCC（Critical Coagulation Concentration）。

实验时，准确移取2 mL稀乳液置于分光光度计的比色皿中，再在每个样品中分别加入不同浓度的电解质溶液，混合均匀后立即放入分光光度计中，测量吸光度值随时间变化情况，作吸光度-时间系列曲线。对每条曲线初始时刻的切线，切线斜率代表该电解质浓度下聚沉的速率常数。当电解质浓度大于临界聚沉浓度时，它们的吸光度-时间曲线基本在同一位置，这一位置的零点切线斜率最大，就是快速聚沉速率常数kf，而其它较小的斜率就是慢速聚沉速率常数k，由kf/k求出稳定因子W的值，将logW与电解质浓度的对数logC作图，得出直线与X轴的交点即是CCC值。

文中所采用分光光度计的测量波长为500 nm的可见光，计数时间间隔为5 s。

2 结果与讨论

2.1 吸光度随时间的变化

实验测量了乳液体系在加入不同浓度的盐以后，溶液的吸光度随时间变化情况如图1所示。

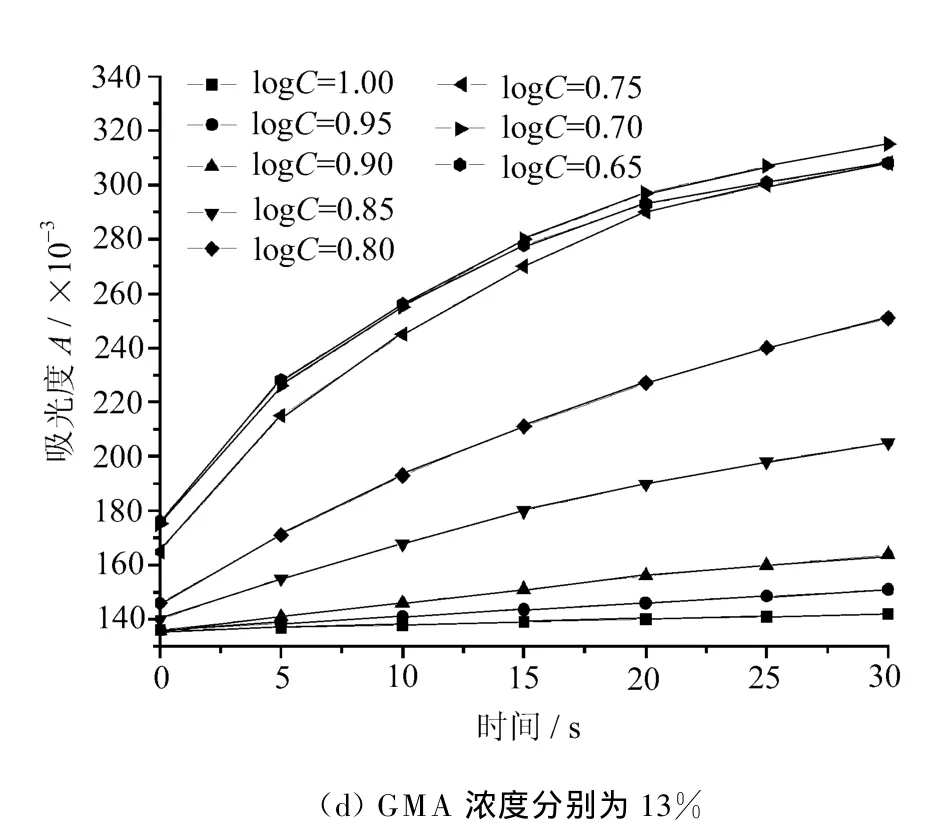
图1 GMA浓度对吸光度的影响

由图1中可见，在GMA含量从0%～13%的多个曲线中，电解质浓度较低时，吸光度随着时间的增大而逐渐增大，二者近似呈线性关系;当电解质浓度较高时，吸光度增加的速度表现为先急后缓的规律，二者不再呈线性关系。

这种变化规律符合DLVO理论。原因是当向乳液中加入较低浓度的电解质溶液时，被沉析出的乳胶粒子较少，它们之间相互碰撞、聚并的机会也比较少，所以吸光度增加的比较缓慢。随着电解质浓度的增加，短时间内被沉析出的乳胶粒子数目较多，它们之间相互碰撞、聚并的机会也比较大，所以吸光度增加的比较快。对较高的电解质浓度来说，电解质的加入很快会使乳胶粒子周围双电层的扩散部分被压缩，并且分散介质中的离子也会被吸附到它们双电层中的Stern层，使双电层的排斥力减小，致使乳胶粒接近到使范德华力占优势的程度，导致乳胶粒子间的聚并能垒为零，此时，乳胶粒子进行以扩散控制的布朗运动，两个乳胶粒碰撞后会不可逆地粘在一起，然后再和其它乳胶粒子碰撞粘连，因此乳液的吸光度迅速增大，直至粘连体受重力作用沉降出来，形成聚沉现象。对于这种乳胶粒子不断形成大的颗粒，而大颗粒又不断从乳液中析出的动态过程，开始时大颗粒形成的速度大于析出的速度，因此乳液的吸光度随时间而增大，直到大颗粒形成与析出的速度达到平衡，乳液的吸光度达到最大值。当电解质浓度达到一定程度时，再增加电解质的浓度，其吸光度对时间的曲线基本一致，说明电解质的浓度已达到临界聚沉浓度。

图1还显示出随着GMA含量的增加，所需电解质的浓度也增加，这充分表明乳液的稳定性也随之增加。

比较曲线组可以发现，当GMA含量小于2%时，吸光度（A）-时间（T）关系曲线线形相同，相同时间点上的吸光度数值基本相等，所得到的CCC值相等，故文中没有一一列出GMA含量小于2%时的 A-T关系曲线。上述现象是由于GMA的含量较低，所提供的环氧基团所具有的水溶性和形成氢键的能力不足以对乳液的稳定性产生明显的影响。

2.2 CCC值的确定

对图1中的每条曲线作初始点的切线，将最大的切线斜率作为kf，其余的切线斜率作为ks，kf和ks的比值即为不同电解质浓度下的稳定因子W的值，再以logW对电解质浓度的对数logC作图，如图2所示。

图2 logW-logC关系曲线

图中直线与直线logW=0的交点即为在乳化剂浓度固定时临界聚沉浓度CCC值的对数。

2.3 GMA含量对CCC值的影响

比较研究GMA含量对CCC值的影响情况。求得的含有不同GMA体系的CCC值如图3所示。

从图3中的CCC值曲线随GMA变化情况可见，GMA含量较低（＜2%）时，对乳液的CCC值影响小，即对乳液稳定性的影响不明显。随着GMA含量的增加，由于氧离子的电负性较强，带电量高，粒子间由于同种电荷的斥力作用不易聚沉，稳定性提高（图中a至c）。而且环氧基团与水形成了氢键键合体系，相当于增大了乳胶粒子的空间立体体积，构成了一个表面富集水分子的水球，增加了乳胶粒子失稳的空间位阻，从而提高乳液的稳定性。当GMA的含量超过2%时，CCC值随GMA含量的增加迅速增大，表明乳液稳定性随GMA含量的增加而增加，GMA的含量为13%时，乳液的CCC值达到0.176 mol/L。

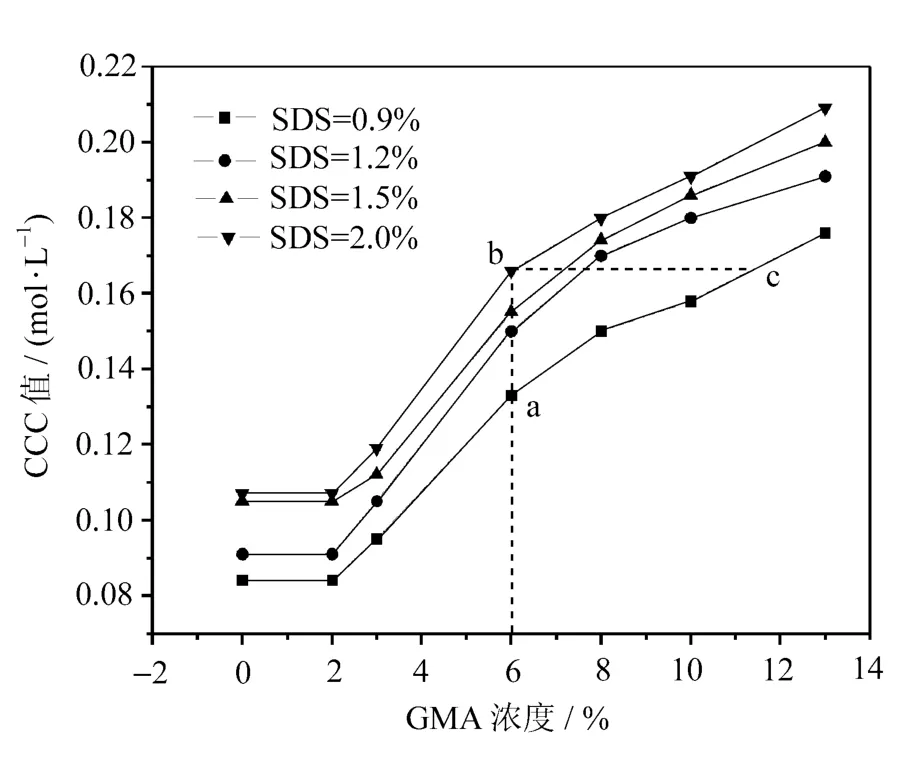
图3 GMA浓度对CCC值的影响

从图3中还可以看到，随着乳化剂浓度的增加，CCC值也随之增加（图中a至b），说明增加乳化剂浓度对提高乳液体系稳定性也十分有益。

综上所述，可以用分光光度法方便有效地测量乳液聚合体系的CCC值，从而定量表征乳液的稳定性。

[1] 张会轩，鲍晓野，杨海东.塑料的增韧机理[J].长春工业大学学报:自然科学版，2002，23（S0）:77-79.

[2] 曹同玉，刘庆普，胡金生.聚合物乳液合成原理性能及应用[M].北京:化学工业出版社，2007:611.

[3] 孟宪谭，朱卫东，张丽红.丁苯胶乳凝胶含量的影响因素[J].橡胶工业，2003，50（6）:348-350.

[4] 接瑜，张毅民，王虹，等.苯丙乳液聚合稳定性研究[J].化学工业与工程，2007，24（1）:40-44.

[5] 凌建雄，涂伟萍，杨卓如.聚丙烯酸酯乳液的合成研究[J].合成材料老化与应用，2000（2）:5-7.

[6] 石海强，何北海.紫外-可见光谱测定马尾松纸浆树脂中甘油三酯含量[J].光谱学与光谱分析，2007，27（1）:135-138.

[7] Davalos-Pantoja L.Colloidal stability of IgG-and IgY-coated latex microspheres[J].Colloids and Surfaces B:Biointerfaces，2001，20（2）:165-167.

[8] 吴广峰，任群，陶悦，等.乳液临界聚沉浓度及其测定方法[J].胶体与聚合物，2007，25（2）:40-41.

[9] Derjaguin B V，Landau L.Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes[J].Acta Phsicochim，URSS，1941，14:633-662.

[10] Verwey E J W，Overbeek J Th G.Theory of the stabilityoflyophobiccolloids[M].London: Elseviev Amsterdan，1948.

[11] Ottewill R H.Emulsion Polymerization[M].Edit by Irja Piirma.New York:Academic Press，1982: 1-47.

[12] Reerink H，Overbeek J Th G.The rate of coagulation as a measure of the stability of silver iodide sols[J].Discuss Faraday Soc.，1954，18:74-84.

[13] Hamaker H C.The London-van der waals attraction between spherical particles[J].Physica A，1937，4:1058-1072.

[14] Smoluchowski M V.Attempt of a mathematical theory for the kinetics of coagulation of colloid solutions[J].Phys.Chem.，1917，92:129-168.

[15] Overbeek，J Th G.Colloid Science[M].Edit by Kruyt H.Amsterdam:Elsevier，1952.