图书馆信息资源数据约简

杨红军

（长春工业大学图书馆，吉林长春 130012）

0 引 言

信息资源挖掘是图书馆信息数据系统的应用与开发。早在20世纪末，信息情报部门就意识到信息系统中的信息量积累越来越大，以致造成信息量爆炸的危险，尤其进入信息时代，这个问题更为突出。如何解决信息系统中信息不断膨胀的问题，不仅是图书馆信息系统本身的研究课题，也是相关部门学科研究方向。

文中运用数据约简方法来证明这一课题，信息系统约简主要是使信息量减少，它将一些无关或多余的信息丢掉而不影响其原有功能，可以设想将约简后的信息情报重新组合而产生新的决策规则，它可能不同于约简前的任何一条规则，但它们能经推理而得到相同或相近的结果[1]。

1 信息系统及其表示

一个信息系统是一个对S=（U，A），其中U是一个非空、有穷、被称为全域的个体集合，A是非空、有穷的属性集合，即对于属性a∈A，有a:U→Va，其中Va被称做属性a的值集;集合V=∪a∈AVa被说成是属性集A的值区域。如果S=（U，A），则 S′=（U′，A′）使得U⊆U′，A′= {a:a∈A}，对u∈U，a′（u）=a（u），并且对a∈A，有Va=Va′，则称S′为S的一个U′-扩充，S被称做S′的子系统;如果S=（U，A），使得A⊆B的S′=（U，B）将被认为是S的一个B-扩充[2-3]。

例1，设全域U={u1，u2，u3，u4，u5}，并设属性A={a，b，c，d，e}，此外，置Va={0，1，2}，Vb= {0，1}，Vc={1，2}，Vd={1，2}，Ve={0，1，2}，则S =（U，A）是信息系统的一个例，见表1。

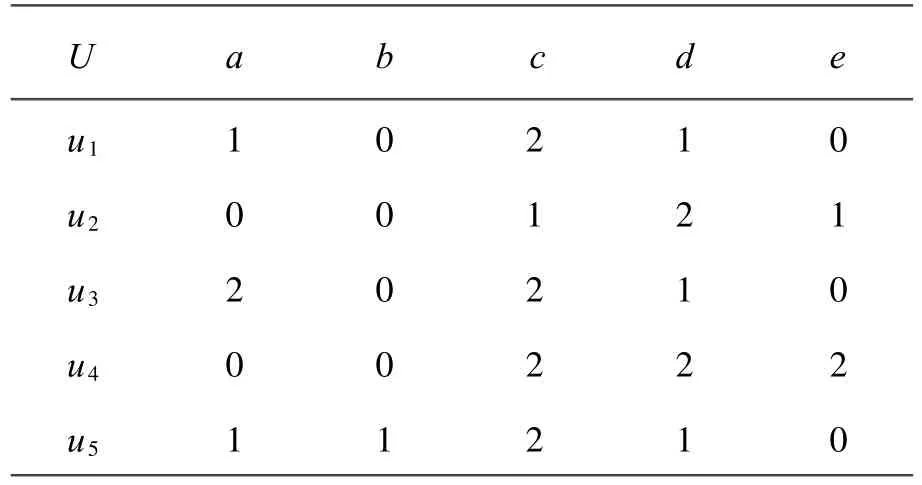
表1 一个信息系统的例子

一般说来，在一个给定的系统中，不能利用系统的属性区别全体单个个体，也就是说，不同的个体关于考虑的属性可以有相同的值。因此，任意属性集可以将U分成类，这些类建立了全体个体集U上的划分。其定义方法如下:

给定一个信息系统S=（U，A），任一子集B⊆A，加上被称为不分明关系的二元关系IND（B）:

注意:IND（B）是一个等价关系，并且IND（B）=∩a∈BIND（{a}）。如果uIND（B）u′，则称个体u和u′关于B中的属性是不可分明的，换句话说，就是不能用B中的属性来区别u和u′。

任一个信息系统S=（U，A）确定一个信息函数:

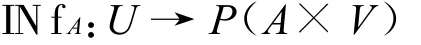
其中，V=∪a∈AVa，它是由 INfA（u）= {（a，a（u））:a∈A}定义的集合;P（X）表示X的幂集，用INF（S）表示信息函数的集合:因此，uIND（A）u′当且仅当 INfA（u）= INfA（u′）。有时，信息函数的值将被表示为向量的形式（v1，v2，…，vk），vi∈Va，对i=1，2，…，k均成立。m=|A|为属性集A的基数，这些向量被称作信息向量。

设S=（U，A）是一个信息系统，其中A= {a1，a2，…，am}，对（a，v）被称为原子，a∈A，v∈V，（a，v）也可写成a=v或av，它被定义在A×V上。A×V上的基是包含原子（a，v）的最小集，并且关于经典命题联结词（～，∨，∧）的运算是封闭的。S上的项τ的语义是|τ|s或简记成|τ|，它被归纳定义如下:

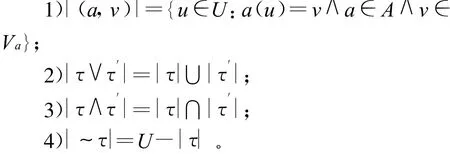
两个项τ和τ′是等价的，τ→→τ′，当且仅当|τ|=|τ′|。

特别有:

设S（U，A）是一个信息系统，又设C，D⊆A是属性集A的两个子集，分别称C和D为A的条件属性和决策属性，如此S被写成T=（U，A，C，D），是一个决策表。

定义1 函数dX:A→V，使得dX（a）=a（x），其中a∈A，X⊆U，x⊂U，称dX是T上的一条决策规则。若a∈C⊂A，则记dX|C是决策规则的条件部分;若a∈D⊂A，则记dX|D是决策规则的结论部分。

定义2 如果对任一个体y≠x，dX|C=dY| C→dX|D=dY|D，称dX是一致的，否则，dX是不一致的。

一致性决策规则说明条件值相同必须隐含着决策值相同，即决策规则完全依赖于条件值。

定义3 如果对所有的决策规则都是一致的，则它们所处的决策表T=（U，A，C，D）是一致的，否则，它们所在的决策表是非一致的。

定义4 设T=（U，A，C，D）是一个决策表，其条件属性和决策属性分别是C和D，称D在T中以程度k（0≤k≤1）依赖于 C，记成C→T，KD[4]。

其中

POSC（D）是D的C-正区域。

1）若k=1，简写成C→TD，在这种情况下，C→TD意味着IND（C）⊆IND（D），在已知条件C下，可将U上全部个体分成D-基本类;

2）若0＜k＜1，则称D Rough依赖于C，在已知条件C下，只能将U上那些属于正区域的个体分成D-基本类。

3）若k=0，则称D全不依赖于C，说明利用条件C在U上没有元素能被分成D-基本类。

命题1 决策表T=（U，A，C，D）是一致的，当且仅当C→TD。

注意:该命题的结果是直截了当的，它也提供了一个检查决策表是否一致的方法，即如果依赖度k=1，则决策表是一致的;否则，是非一致的。

命题2 每个决策表T=（U，A，C，D）都能惟一地分解成两个决策表T1=（U1，A，C，D）和T2=（U2，A，C，D），使得在 T1中C→T1，1D而在T2中C→T2，0D。

其中

如果一个决策表是不一致的，则根据命题2，可将其分解成两个子表 T1和T2，其中一个是一致的，依赖度k=1;另外一个是全不一致的，其依赖度k=0。

例2，考虑非一致决策表，其中 T=（U，A，C，D），C={a，b，c}，D={d，e}。A= C∪D，分别称C和D为条件属性集和决策属性集，见表2。

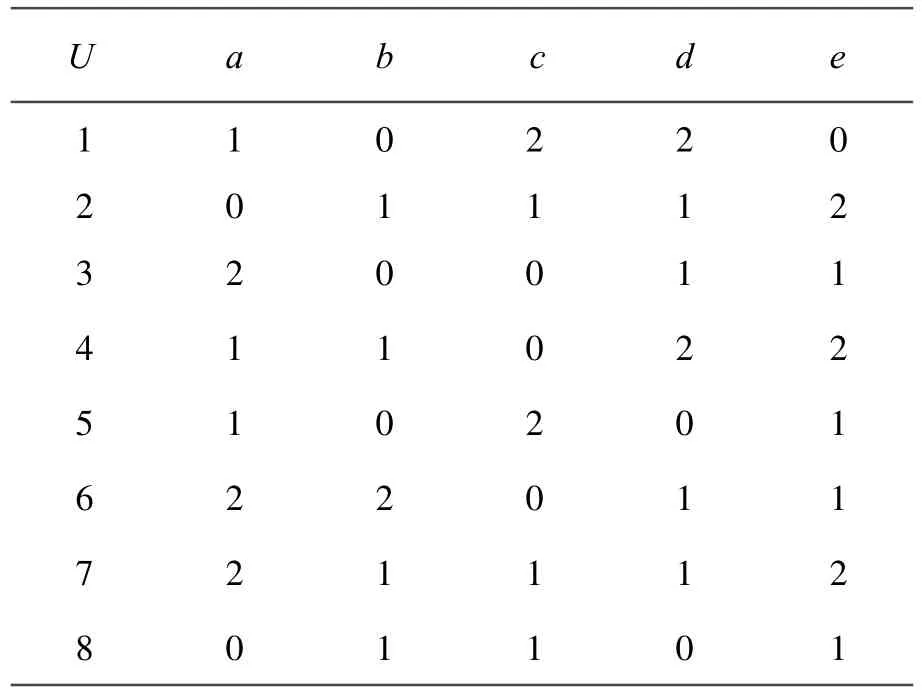
表2 非一致决策表

根据命题2，可将表2的T=（U，A，C，D）分解为一致决策表T1=（U1，A，C，D）和全不一致决策表T2=（U2，A，C，D），分别见表3和表4[5]。

表3 一致决策表（T1=（U1，A，C，D））

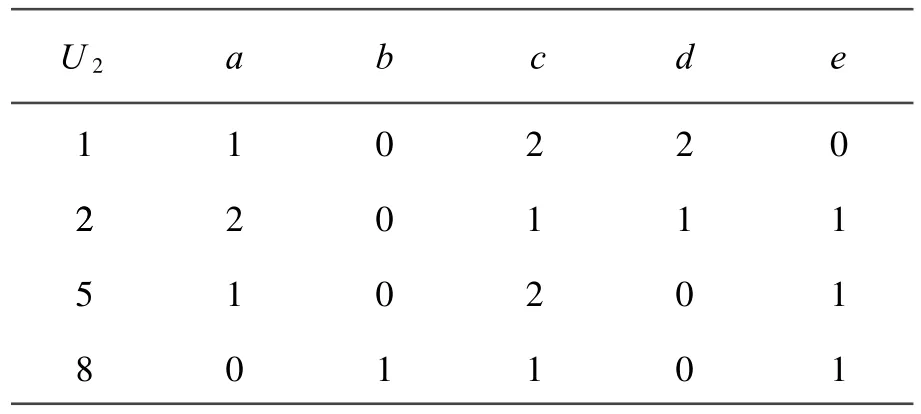
表4 全不一致决策表（T2=（U2，A，C，D））

2 属性约简的数据分析方法

决策表的简化一般有属性约简（等价于从决策表中消去一些不必要的列）和属性值约简（等价于从决策表中消去一些无关紧要的属性值）[1]。

定义5 从信息系统的决策表中，将属性集A中的属性逐个移去，每移去一个属性即刻检查其决策表，如果不出现新的不一致，则该属性可被约去;否则，该属性不能被约去，称这种方法为属性约简的数据分析方法。

例3，T=（U，A，C，D），其中，C={a，b，c}，D ={d，e}（A=C∪D）分别称为条件属性集和决策属性集，见表5。

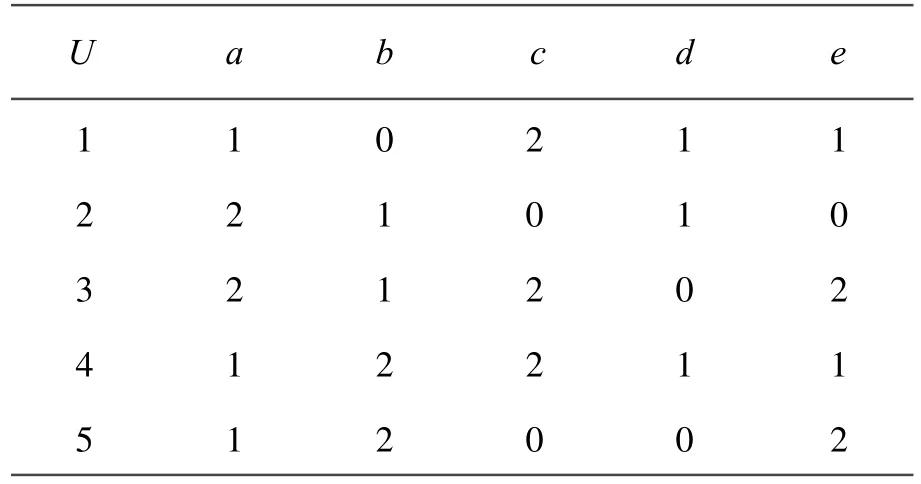
表5 一致决策表

它们的规则如下:

显然表5是一致性决策表，因为其中每条规则都是一致的。为了计算条件属性的约简，我们就一致表和非一致表分别讨论。

对一致表约简，可逐个移去条件属性并即刻检查决策表是否一致[6]。

从表5移去属性a∈A，得到的决策表也是一致的，见表6。

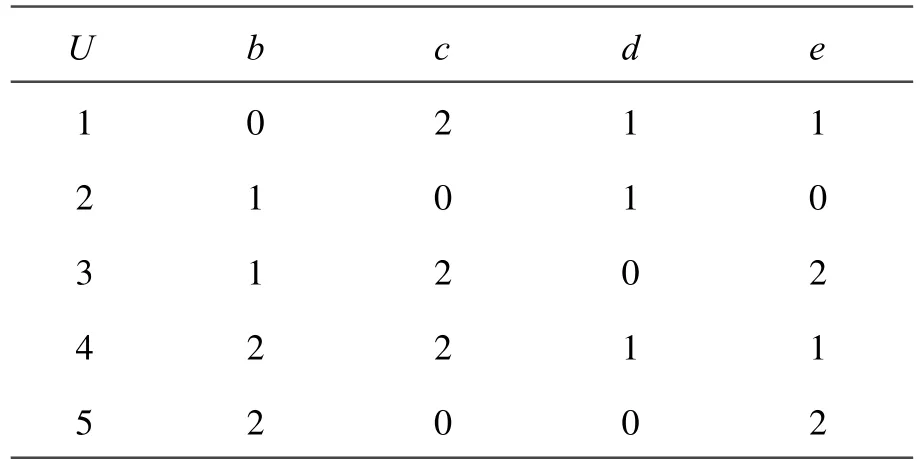
表6 一致决策表（移去属性a）

从表5移去属性b得到的决策表也是一致的，见表7。

表7 一致决策表（移去属性b）

从表5移去属性c，得到不一致决策表，见表8。

表8 不一致决策表（移去属性c）

因为第2条规则a2b1→d1e0和第3条规则a2b1→d0e2，根据定义2，它们是矛盾的;同理，第4条规则和第5条规则也是不一致的。因此c是条件属性集{a，b，c}中的核，而a和b都可被约去，由此得到两个约简（分别见表6和表7）[7]:

对非一致决策表，其计算约简可用类似于一致决策表的方法，也就是逐个移去属性并检查决策表是否出现新的不一致。如果产生新的不一致决策规则，则该属性是核，不能被约去;否则，不是属性集的核，可以被约去。形式地，∀a∈C，如果POSC（D）=POS（C-|a|）（D），其中，C和D分别为条件属性和决策属性集，则属性a是条件属性集C中可被约去的;否则，a是C中的核，不能被约去。

定义6 设B⊆C，如果对∀a∈B都是不可被约去的，则B关于D是独立的;而任意C′⊇B都是关于D相关的，所以B称为D-约简;全体不可被约去的属性集被称为核集。

例如，不一致决策表8，其条件属性集C= {a，b}和决策属性集D={d，e}。在该决策表中惟一一条一致决策规则是第1条a1b0→d1e1，因此，该决策的正区域由一条规则组成。

为了计算属性a和b是否是可被约去，移去每个属性并检查该正区域是否会被改变。如果会被改变，则该属性不能被约去;如果不会被改变，则该属性可能被约去[8]。

对表8移去a，得到不改变正区域决策表，见表9。

表9 不改变正区域决策表

表9与表8有相同的正区域。

从表8中移去b，得到改变正区域决策表，见表10。

表10改变了表8中的正区域，使得它所有决策规则都不一致，即正区域为空。b是核，其约简是惟一一个RED（C，D）={{b}，{d，e}}，也就是说，经约简后的决策表是表9的形式，至此，对图书馆信息数据库约简推理论证这种简化查找信息的方法可以避免生成多余的中间环节，无疑也节省了存储空间，故在时间上得到了节省。

表10 改变正区域决策表

[1] 于海涛.Rough集理论在数据约简中的应用[J].安徽教育学院学报，2004（5）:21-23.

[2] 姚健.图书馆信息化探识[J].中国图书馆学报，1995，21（3）:63-68.

[3] 宋恩梅.信息资源管理研究的多重视角极其共同体的形成[J].中国图书馆学报，2007（5）:64.

[4] 霍红梅，杨达.信息管理研究的制度分析方法[J].现代情报，2007（11）:26-28，31.

[5] 杨启帆，李哲宁，王聚丰，等.数学建模例集[M].北京:高等教育出版社，2006.

[6] 谢兆鸿，范正森，王艮远.数学建模技术[M].北京:水利电力出版社，2003.

[7] 李志林，欧宜贵.数学建模及典型案例分析[M].北京:化学工业出版社，2006.

[8] 袁新生，邵大宏.在数学建模中的应用[M].北京:科学出版社，2007.