停车需求预测结果评价中的可拓层次分析法

王维民

(围场县交通局地方道路管理站)

1 引 言

目前,对停车预测结果的对比中多采用文字的描述,没有定性和定量的综合分析,方法评价中调查资料的准确性、泊位满足度和投资费用三个方面给出预测结果优劣比较,采用实用、有效的可拓层次分析法(EAHP),研究在相对重要性程度不确定时 AHP如何构造判断矩阵的方法。并弥补了以往模糊AHP方法通常不考虑判断矩阵的一致性方面的缺欠,将求符合一致性要求的判断矩阵权重向量的方法有机地融合到可拓AHP方法中去。

可拓学的理论支柱是物元理论和可拓集合理论,其逻辑细胞则是物元。可拓集合和物元概念能根据事物关于特征的量值来判断事物属于某集合的程度(即评价事物的好坏、方案的优劣),而采用扩展到(-∞,+∞)的关联函数值能使评价精细化、定量化,从而为解决从变化的角度进行方案评价的问题提供了新途径。层次分析法(AnalyticHierarchy Process,简称AHP)是将半定性、半定量问题转化为定量问题的有效途径,它将各种因素层次化,并逐层比较多种关联因素,为分析和预测事物的发展提供可比较的定量依据。

2 可拓层次法

2.1 可拓层次分析法的改进

可拓层次分析法在构造判断矩阵时,指派 1～9整数及其倒数的标度时,将人判断的模糊性考虑进来。具体地说,在两两比较方案重要性的赋值时,传统的层次分析法只考虑人的判断的两种极端情况。在实际判断中,人的判断往往是在一个范围内,例如,甲乙两个方案相比时,经常认为甲方案比乙方案重要程度在 4.5～5.5之间,这更接近实际。用扩展到(+∞,-∞)的关联函数值能使评价精细化、定量化,从而为解决从变化的角度进行方案评价的问题提供了新途径。基于可拓集合理论和方法,研究在相对重要性程度不确定时AHP如何构造判断矩阵的方法,弥补了以往模糊AHP方法通常不考虑判断矩阵的一致性方面的缺欠。

2.2 构造可拓判断矩阵

应用 EAHP方法时,在建立了层次结构之后,针对第k-1层的某一个(例如第h个)因素或准则,将第k层与之有关的全部 nk个因素,通过两两比较,利用可拓区间数定量表示它们的相对优劣程度(或重要程度),给出所有的两两比较的元素,从而构造一个可拓区间数判断矩阵A。

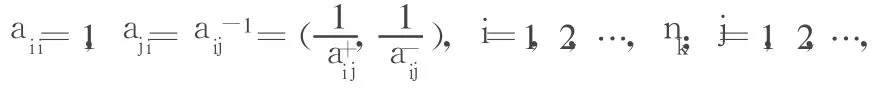
2.3 计算综合可拓判断矩阵和权重向量

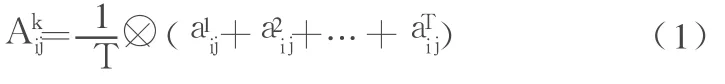
求得第k层的综合可拓区间数,由此得到第k层全体因素对第k-1层次的第h个因素的综合可拓判断矩阵。

对上述第k层综合可拓区间数判断矩阵A=(A-,A+),求其满足一致性条件的权重向量的步骤为:

(1)求的最大特征值所对应的具有正分量的归一化特征向量。

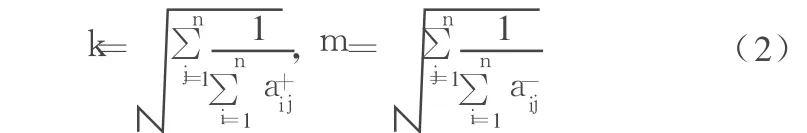
(3)求出权重向量

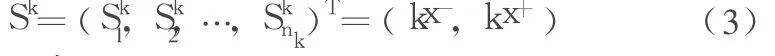
2.4 层次单排序

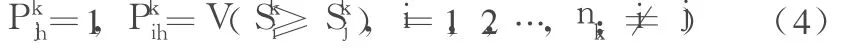
2.5 层次总排序

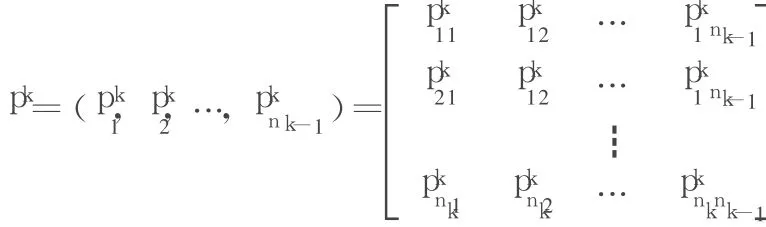
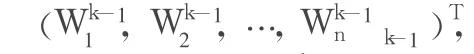
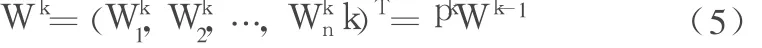
并且一般地有

这里W2实际上就是单排序向量。

3 可拓层次分析法的应用

通过对天津市滨海新区停车调查,分别有机动车与人口预测、机动车分类预测和用地分析预测三种方法,总结出预测的方法以及规划年需求的泊位数,如表 1。

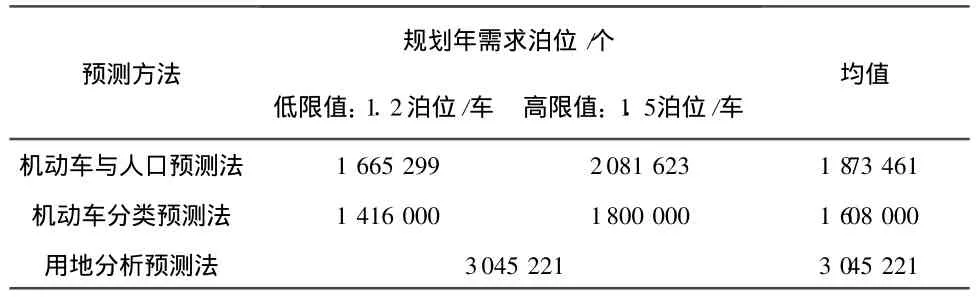
表1 预测方法与规划年需求泊位

根据调查来的有限资料来预测停车需求,三种方法中都存在调查资料的准确性、泊位满足度和投资费用等影响其方法可靠性的因素,本文就这三个因素作为可拓层次分析法中准则层的因素来进行评价决策。

建一个专业的停车场或停车楼投资都需要几十万上百万,按目前一个车位平均 3万元钱计算。滨海新区建成面积,是规划建成面积的 0.49,土地利用预测法中是以规划建成面积来预测的,因此调查资料的准确性仅为 0.49。其他因素的指标详细见表 2。

表2 各方法因素值表

3.1 建立层次结构

三个预测方法各有优势,需要综合几个方面的因素进行评价决策,以选择最优结果为决策目标 A;准则层的因素包括调查资料的准确性 C1,泊位满足度C2,投资费用 C3等 3项;方法层包括方法P1、方法P2和方法P3。建立层次结构模型,见图 1。整个计算过程都是围绕层次结构图展开的。

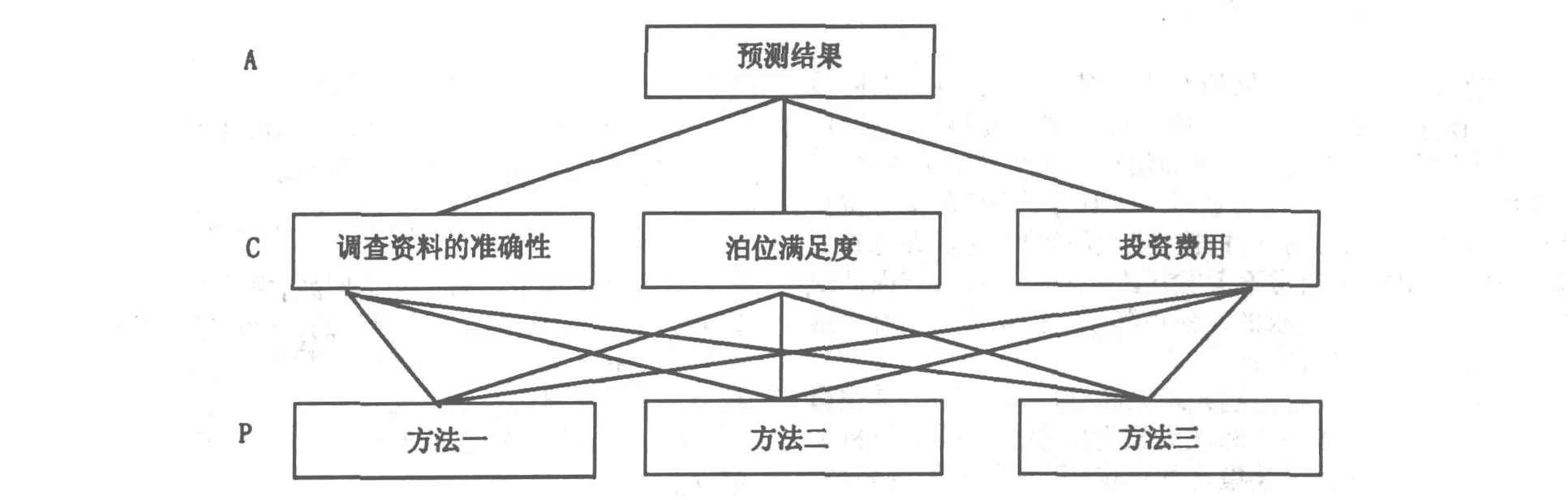
图1 层次结构模型

3.2 制定判断标度

在构造可拓区间数判断矩阵的过程中,我们采用 1-9的比例标度表示法,具体给出规则如表 3。

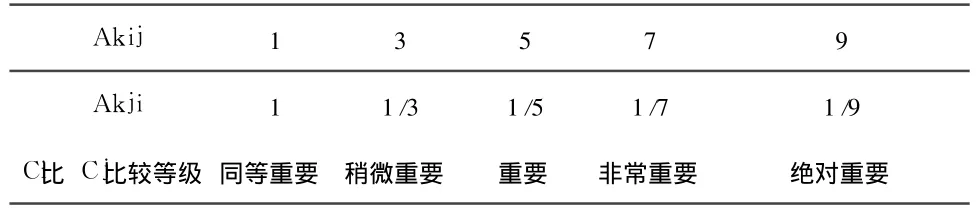
表3 相对比较比例标度

3.3 构造决策层对目标层的可拓判断矩阵并排序

首先给出两个专家对评价因素的打分情况,见表 4。

表4 专家一和专家二的打分表

由(1)式得到可拓判断矩阵:

首先求x-,x+:

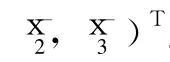
从而计算出了x-=(0.763,0.161,0.076)T,同理可得x+=(0.740,0.177,0.083)T。

由(2)式和(3)式得到k=0.971,m=1.017,从而可得S1=＜0.741,0.753＞,S2=＜0.156,0.180＞,S3=＜0.074, 0.084＞,于是V(S1≥S3)=61.727,V(S2≥S3)=9.636,则根据公式(4)得

从而得到三个评价指标相对总目标的单排序:P= (0.853,0.133,0.014)T。

3.4 构造各个方案层对于评价准则的判断矩阵并排序

由表 2给出的各个评价指标的因素值,应注意到三个评价指标在数量大小上所标示的含义不同,因此需要进行转换,转换后通过两两比较得到表5。

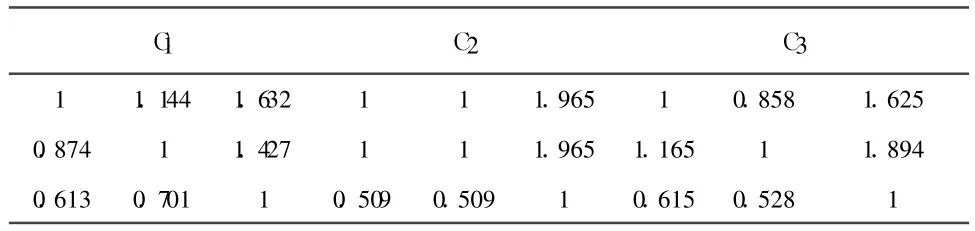
表5 方案层对准则层的判断矩阵

按照(3)的处理方法,对此判断矩阵进行相同的运算,得出方案层对准则层的单排序,排序结果见表 6,总排序见表7。

表6 各准则层方案层的单排序

表7 各准则层方案层的总排序

以上的排序说明机动车和人口预测方法最优。只考虑了调查资料的准确性、泊位满足度和投资费用三个因素,这对结果的评价精度有一定的影响,如果考虑的因素更多,则精度会更高,决策也更准确。

4 结 论

运用可拓集合理论和方法,对传统的层次分析法(AHP)中构造判断矩阵的方法进行改进,克服了以往的AHP方法在构造判断矩阵时不考虑矩阵的一致性方面的缺陷,并应用到停车预测中,得到了满意的结果,使得可拓层析分析法(EAHP)能够更有效的决策评价。

[1] 蔡文,杨春燕,林伟初.可拓工程方法[M].北京:科学出版社, 1997.

[2] 徐学珍,赵尘,孙微微.模糊层析分析法在公路环境影响评价中的应用[J].西南林学院学报,2006,(1).

[3] 鞠红.可拓数学方法在供应链管理中的应用研究[J].大连海事大学,2003.

[4] 杨春燕,张拥军,蔡文.可拓集合及其应用研究[J].数学的实践与认识,2002,(2).

[5] 张吉军.模糊层次分析法[J].模糊系统与数学,2001,(2).

[6] 高洁,盛昭瀚.可拓层次分析法研究[J].系统工程,2002,(5).