基于动力学与分形分析的絮凝控制新指标

赫俊国，魏希柱，姜 涛，张 杰

(哈尔滨工业大学市政环境工程学院，哈尔滨150090，junguohe@263.net)

絮凝是水处理系统的关键工艺单元.絮凝动力学的控制一直是水处理界研究的难点与热点［1－2］.絮凝的实质是使混合工艺中析出的絮凝体凝结，并达到一定的尺度与密实度，从而有利于沉淀，实现清浊分离的目的，它对后续沉淀工艺的效能和水厂运行有极为重要的影响［3］，其中絮凝工艺动力学控制与絮凝体形态控制一直受到国内外广泛关注.

在目前的絮凝动力学以及絮体形态学研究中，水体流动的速度梯度(G)是核心，而速度梯度在理论推导与实际应用中仍然存在较大缺陷［4］.例如关于速度梯度，目前应用的是基于层流推导出的牛顿内摩擦公式，而在絮凝工艺中的水流总是处于湍流状态，除前进速度外，还存在纵向和横向脉动速度［5］.因此，将基于层流推导出的模型应用于复杂的紊流絮凝过程，是不适宜的.在工程实践中，网格絮凝应用广泛，在网格后面的一定距离处，水流近似处于均匀各向同性湍流状态，即在这个区域中不同的空间点上水流平均速度梯度为零，按照速度梯度理论，网格絮凝池效率应最差，而事实是网格絮凝池的反应效果却优于廊道式反应设备［6］.因此，速度梯度理论在理论和实际应用上有不足，其并未揭示絮凝的动力学本质，而在絮凝形态学研究中，多是以速度梯度为动力学控制指标，对絮凝体进行分形分析，其过程的形态描述亦有缺陷.

动力学传质过程控制，是开发经济高效絮凝工艺所要解决的关键技术问题，但至今未能得到很好的解决［7－8］，本文通过对絮凝工艺的动力学传质过程和絮体强度控制影响因素的分析，利用数学分析的方法，提出一个基于动力学与形态学分析的新指标，用于评价和控制絮凝工艺效果.

1 湍流水体中絮凝体的动力学分析

絮凝工艺中的水体呈紊流运动，含有无数大小杂乱无章的涡旋，涡旋的轴向及涡旋间的相对运动速度是随机变化的，不同尺度的涡旋相互叠加，并不断地产生、发展、衰减与消失，对涡旋和其中絮凝体进行分析与控制，是絮凝过程动力学控制的关键.

设絮凝体的有效半径为r0/m，絮凝体与水流相对速度为u/(m·s－1)，水的密度为ρ/(kg· m－3)，絮凝体密度为ρ0/(kg·m－3)，则单位质量球形絮凝体所受的水力阻力为

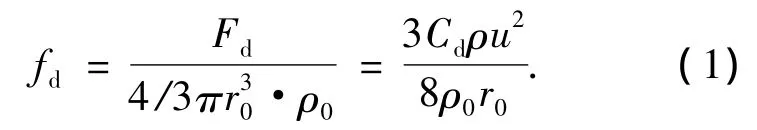
如果略去因絮凝体尺寸不同而造成的密度变化，由式(1)可见，单位质量球形絮凝体所受水力阻力随尺度增大而减少，即絮凝体越大单位质量所受水力阻力越小.当水流作涡旋运动时，在离心惯性力作用下，固体絮凝体沿径向与水流产生相对运动.不同尺度絮凝体在湍流涡旋中所受离心惯性力是不同的，这个作用将增加不同尺度絮凝体在湍流涡旋径向碰撞的几率.在湍流涡旋中取一个小的脱离体，显然，沿径向方向作用在该脱离体上有两个力:即离心力和压力，两者相平衡，如果把坐标原点取在运动涡旋的中心上，则有

假设与该脱离体同一位置有一与水流同步运动的絮凝体，其所受压力合力为ρ·(u/r)，所受的离心力为ρ·(u/r)，该絮凝体所受净离心力则为离心力与压力之差，即絮凝体在其作用下沿涡旋的径向运动，所受水力阻力即为液体对其拖动力.而式(1)表明，絮凝体尺度越大、跟随速度与其所在位置液体的速度差越大，则单位质量所受离心力越小.在一个特定的湍流涡旋中的某一个位置必然存在一个特定直径的絮凝体，它所受的离心力与压力合力正好相等.用λ表示涡旋尺度，ε表示单位水体的能耗，则涡旋的雷诺数为Re=uλ/ν，其中ν=μ/ρ，为水的运动粘滞系数.涡旋雷诺数表示涡旋的惯性力与粘性力之比，当两者相等时，涡旋尺度特征值［9］λ0满足uλ0/ν=1，则有λ0=(ν3/ε)1/4;当涡旋尺度λ＞λ0，涡旋中的惯性力是主要的，而粘性力可忽略，此时涡旋中速度的特征值uλ主要与ρ、λ、ε3个因素有关，由三者组成的速度因子 (ελ/ρ)1/3可决定uλ的量级，表示为uλ∝(ελ/ρ)1/3;当λ＜λ0时，则有当λ＞λ0时，涡旋的特征周期Tλ只与 ρ、λ、ε有关，其量级由时间因子(ελ2/ρ)1/3决定，即

而涡旋的速度特征值为

则涡旋的加速度特征值为

由式(2)可知，涡旋的加速度随涡旋尺度减少而增加，当涡旋尺度达到特征值λ0时，其加速度最大，惯性效应最强，不同尺度絮凝体沿径向碰撞的几率最高，絮凝效率从而可以得以保障.可以说，湍流中的微小涡旋的离心惯性效应是絮凝重要的动力学致因.

2 絮凝动力学控制指标的数学分析

絮凝过程的主要影响因素包括:反应设备型式、反应池空间尺度、流体空间流速、流体黏度与密度、絮凝体的数量浓度、能耗.对于反应设备而言，絮凝的影响因素为反应设备单元格的尺寸L/ m、反应设备横截面宽度b/m、空间流速u/(m· s－1)、絮体密度ρ0/(kg·m－3)，水体密度ρ/(kg ·m－3)、水体黏度μ/(Pa·s)、絮凝体的量N/ (个·m－3)、能量损失h/m等［10］，即絮凝过程包含有8个物理量，即

设流体为不可压缩的，以L、u、ρ为基本量，则有

式(3)中的π1，π2，π3，π4，π5可以用基本量表示为

其中量纲取国际标准，即L=［L］、U=［L］［T］－1、ρ=［M］［L］－3，其行列式为

采用量纲和谐原理［10］计算得

将其带入式(3)，则

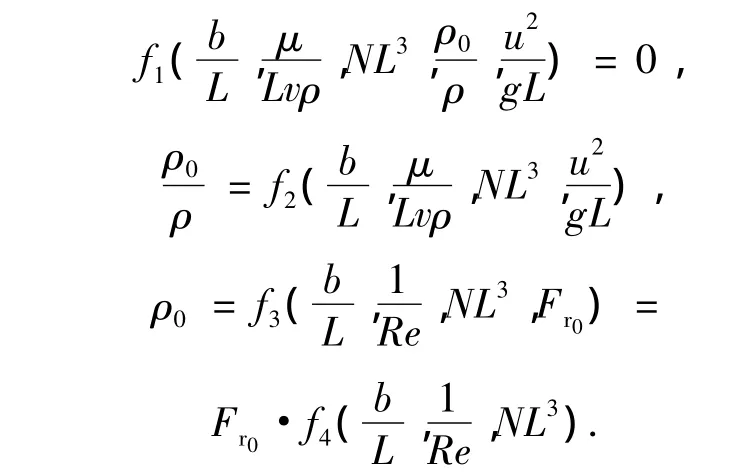
式中:Fr0为剪切强度;λ'为变量参数，

3 絮凝体强度的推求

在一定的水力条件下，絮凝体粒径由两个相反的力控制，即絮凝体的粘结力和流体对絮凝体的破碎力.絮凝体的粘结力B/(g·cm·s－2)与絮凝体的净截面积A/cm2成正比［11］，即B∝A.对于一个直径为r0的絮凝体，其净面积为

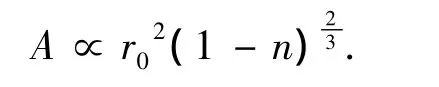
也即

则絮凝体的质量为

式中:ρ0、ρ、ρ'分别为絮凝体(含水)、水和絮凝体(不含水)的密度(kg·m－3)，n为孔隙率(%)，V0为絮凝体体积(m3)，V为絮凝体中水分的体积(m3).絮凝体密度与絮体直径及其分形维数(Kp)的关系可描述为［11］

由式(5)、(6)和式(7)可得絮凝体的粘结力B为

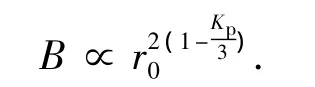
由于水体涡旋的剪切作用，絮凝体自身具有破碎倾向.涡旋作用在絮凝体上的最大外部破碎力，就是作用在直径为r0的絮凝体上相对两侧单位面积上的动力差.根据Kolmogomff的各向同性理论，总的破碎力ΔF在惯性区可以表述为［12］

在粘性区则表述为

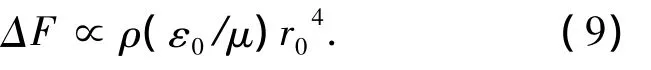
絮凝体的破碎一般发生在粘性区域，其临界条件是破碎力与粘结力相等.

则絮凝体的强度kσ可描述为B与ΔF的函数，即

即

4 Fr0作为絮凝控制指标合理性的讨论

在絮凝工艺中，所形成的絮凝体过大，其密度将趋近于水，沉淀效果就差;反之，所形成的絮凝体过小，其密度将趋近于分子或分子团密度，受水流脉动的影响很大，沉淀效果也不会好.式(1)表明，絮体絮凝体的尺度越大，受水流脉动的影响越小，沉淀效果越有保证;而式(8)和式(9)表明，絮凝体的尺度越大，越容易破碎.因此，将絮体絮凝体控制在一定的尺度范围，对于保证絮凝沉淀的效果是非常重要的.

絮凝动力学控制指标的数学分析证明，通过控制λ'和Fr0可以控制絮体密实度.在式(4)中，λ'被表述为反应设备的形式、单位体积的絮体絮凝体数和水体湍动度的变量函数.其中，b/L是设备形式参数，可控制微涡旋的尺度，设备形式确定时，其值也是定值;NL3是原水絮凝体浓度，对λ'将有显著影响，但在水质变化幅度不大时，可认为是定值;对于形式确定的反应设备，一旦反应池中的流速分级一定，则水体单位体积的Re不变.在设备及速度分级确定后，水体单位体积的絮凝体数就成为影响λ'的主要因素.也就是说，当水质和投药量变化时，将影响λ'的取值范围，进而对ρ0产生影响.在不同的水质和投药量下，改变Fr0即可对絮体的密度进行控制，进而控制反应效果.

式(10)表明，絮凝体的强度反比于微涡旋的特征值Fr0，同时是絮凝体特征尺度的函数.随着Fr增大，絮凝体变小，密度增加，Kp增大，f(r0)总体上呈上升趋势;Fr减小，絮凝体尺度变大，密度减小，Kp变小，f(r0)总体上呈下降趋势.因此，增加能耗，即提高水体的剪切强度，可以破坏絮凝体，减小絮凝体强度，因此，一味增加能耗对絮凝不一定有利.当絮凝体的强度不变时，剪切增大，f(r0)随之增大，即，絮凝体尺度或分维增加.而防止絮体破碎，应增加絮凝体的强度，同时保证絮凝体达到一定的尺度与分形维数，而剪切强度的增加导致絮凝体有缩小的趋势，絮凝体强度增加，因此，保证适当的剪切强度并同时控制絮凝体的尺度与分形是非常关键的，即随着絮凝进程，控制一定的Fr0是工程实施的关键.关于Fr0的控制范围在下一步的试验研究中确定.

5 结论

1)提出一个基于动力学与形态学分析的新絮凝控制指标Fr0，Fr0是一个控制絮凝体尺度和密实度的理想控制指标，对其有效控制是获得良好絮凝效果的关键，Fr0可作为絮凝过程控制的新动力学指标.

2)湍流水体微小涡旋的离心惯性效应是絮凝的动力学致因，特征尺度量级的涡旋在其中发挥着重要作用.

3)水流的剪切强度Fr0不仅决定着絮凝体密度(ρ0=λ'Fr0)，而且控制着絮凝体强度［kσ∝

［1］ZONDERVAN E，BLANKERT B，BEN H L，et al.Development of a multi－objective coagulation system for long－term fouling control in dead－end ultrafiltration［J］.Journal of Membrane Science，2008，325(2): 823－830.

［2］YAN Mingquan，WANG Dongsheng，QU Jiuhui，et al.Relative importance of hydrolyzed Al(III)species(Ala，Alb，and Alc)during coagulation with polyaluminum chloride:A case study with the typical micro－polluted source waters［J］.Journal of Colloid and Interface Science，2007，316(2):482－489.

［3］DAS K K，SOMASUNDARAN P.A kinetic investigation of the flocculation of alumina with polyacrylic acid［J］.Journal of Colloid and Interface Science，2004，271 (1):102－109.

［4］赫俊国.饮用水混凝工艺动力学分析与试验研究［D］.哈尔滨:哈尔滨工业大学，2005.

［5］CHEN Yanxiao，LIU Shaoying，WANG Gongying.A kinetic investigation of cationic starch adsorption and flocculation in kaolin suspension［J］.Chemical Engineering Journal，2007，133(1/3):325－333.

［6］赫俊国，赵连栋.涡旋混凝低脉动沉淀技术在海港水厂的应用［J］.给水排水，2002，28(l):42－45.

［7］SOOS M，SEFCIK J，MORBIDELLI M.Investigation of aggregation，breakage and restructuring kinetics of colloidal dispersions in turbulent flows by population balance modeling and static light scattering［J］.Chemical Engineering Science，2006，61(8):2349－2363.

［8］GREGORY J.Monitoring particle aggregation processes［J］.Advances in Colloid and Interface Science，2009，147/148:109－123.

［9］严煦世，范瑾初.给水工程［M］.北京:中国建筑工业出版社，2003.

［10］ZEYBEK Z，KARAPINAR T，ALPBAZ M，et al.Application of adaptive heuristic criticism control(AHCC)to dye wastewater［J］.Journal of Environmental Management，2007，84(4):461－472.

［11］POERSCHMANN J，TROMMLER U，NYPLOVA P，et al.Complexation—flocculation of organic contaminants by the application of oxyhumolite－based humic organic matter［J］.Chemosphere，2008，70(7):1228－1237.

［12］许保玖，安鼎年.水处理理论与设计［M］.北京:中国建筑工业出版社，1992.