基于RST和SVM的中文问题分类方法

董云耀,陈小翠,黄 炜

(杭州电子科技大学计算机学院,浙江杭州310018)

0 引 言

所谓问题分类就是在中文问答系统(Chinese Question Answering System,CQAS)中按预定的分类规则确定问题的类型[1,2]。支持向量机(Support Vector Machine,SVM)是一种针对数据分类和回归问题的统计学习理论,但是它不能处理冗余数据,而且当训练样本数量过大、空间维数过高时会导致训练时间过长、处理速度过慢,降低分类的效率[3,4]。粗糙集理论(Rough Set Theory,RST)[5]中的属性约简可以删除信息系统中的冗余属性,降低数据空间维数,但是它只能处理量化数据,而且它的容错能力和泛化能力也比较弱,这正是支持向量机的优势所在。因此,本文利用RST和SVM的优点及两者之间的互补性,提出了一种新的问题分类方法CRV(The Chinese question classification based on RST-SVM),利用RST中属性约简方法消除冗余的属性,降低了样本维数,将约简后的数据利用SVM进行分类,从而得到了较高的分类精度。并将该方法应用于计算机网络课程的自动问答系统中,以验证该方法的可行性。

1 相关理论

1.1 RST的属性约简

粗糙集理论的属性约简就是在保持分类能力不变的情况下,删除其中不必要或者不重要的属性[6]。其相关定义如下:

定义1 信息系统S=(U,R,V,f)。其中:U={x1,x2,…,xn}为论域;R是属性的非空有限集合,R=C∪D且C∩D=∅,其中C称为条件属性集,D称为决策属性集;V为属性值的集合;f:U×R→V是一个信息函数,它指定U中每一个对象x的属性值;

定义2 设R是U上的等价关系,r∈R,若ind(R)=ind(R-{r}),则称关系r在R中是不必要的,否则是必要的。若每一个r∈R在R中是必要的,则称r是独立的,否则称r是依赖的或非独立的。设Q⊆R并且Q是独立的,且ind(Q)=ind(R),则称Q是R的一个绝对约简,通常R有多个约简,可以将所有约简的交集成为核,记作core(R);

定义3 设P和Q是U中的等价关系,Q的P正区域是U中所有根据分类U/P的信息可以准确划分到关系Q的等价类中去的对象集合,即则称r为P中Q不必要,否则r为P中Q必要的。若P的Q独立子集S,S⊂P有POSS(Q)=POSp(Q),称S为P的Q相对约简。P的所有Q约简的交集称为P的Q核,记为coreQ(P)。P的Q核是P中所有Q必要的原始关系构成的集合;

定义4 令决策表S=(U,R,V,f)中,P,Q⊆R,当且仅当ind(P)=ind(Q)时,Q依赖于P(记作P⇒Q),而当k=γP(Q)=|POSp(Q)|/|U|称Q是k(0 k 1)度依赖P(记作P⇒kQ),γP(Q)是Q与P之间的依赖度;

定义5 在已知条件属性B的前提下,一个属性c∈C-B关于决策属性D的属性重要性定义为:EB(D)=γB∪{c}(D)-γB(D)。

1.2 支持向量机

SVM就是通过用内积函数定义的非线性映射将输入向量映射到一个高维空间,然后在这个高维空间中构造最优超平面作为分类判别平面,使得两类数据样本之间的间隔最大。

假设给定数据样本(x1,y1),…,(xi,yi),xi∈Rn,yi∈{-1,+1},其中i=1,2,…,n,分类面方程为ω◦x+b=0,要使分类间隔最大,就要求2/||ω||最大,而要求分类面对所有样本正确分类,就要求满足:yi(ω×xi+b)≥1,i=1,2,…,n,。根据拉格朗日函数和最优化条件,得到最优分类函数为:f(x)=

常用的核函数有:q次多项式函数、径向基函数和Sigmoid函数。本文采用径向基函数作为SVM的

2 CRV分类方法

本文提出的CRV分类方法首先利用RST决策表中的属性约简,删除问句中那些不重要属性以便降低数据的维数,然后利用SVM分类器对约简后数据进行训练和分类测试,并给出最终的分类结果,其流程图如图1所示。

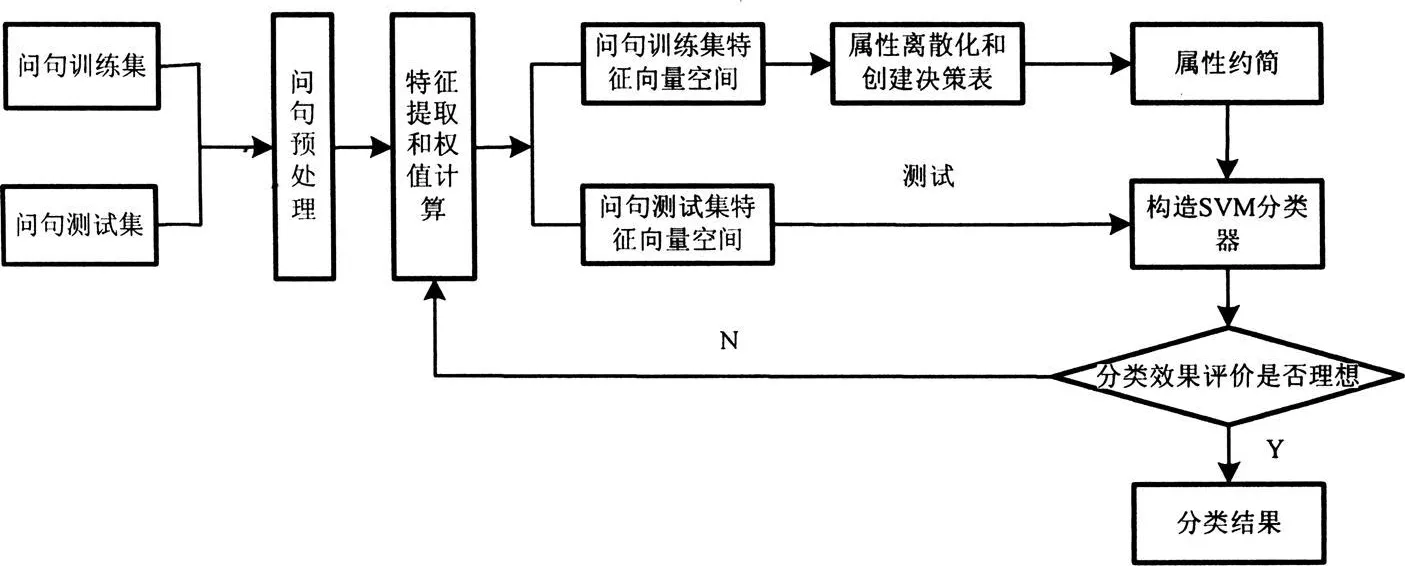
图1 CRV分类流程图

由图1可以给出CRV方法的具体步骤:

(1)问句训练集和问句测试集。从问题库中抽取问句样本集,以大约2∶1的比例将其分为问句训练集和问句测试集,并对问句训练集人工预先分类;

(2)问句预处理。对问句集进行分词、词性标注、去掉停用词、句法分析等预处理;

(3)特征选取和权值计算。由于问句包含的特征信息也较少,因此需要从问句中尽可能多的选取对分类有帮助的特征词,以便于正确的对问题分类。本文选择疑问词、主要谓语动词、中心名词及其之间的依存关系作为问句的特征项,利用TF-IDF方法计算特征项的权值;

(4)特征向量空间。将问句训练集和测试集表示成计算机可以处理的问句向量形式;

(5)属性离散化和创建决策表。由于问句集的属性值是连续的,而粗糙集只能处理离散属性值,因此需要要对问句集进行离散化处理。本文采用等频率离散划分法,根据权值的大小进行排序,将其平均划分成6段,每段用0,1,…,5表示。根据离散化后的属性创建决策表,将每一个问句作为决策表中的一行,特征项构成决策表的条件属性,离散化后的属性值作为条件属性的取值,问句所属的类别为决策属性,对其中的每一个类别赋予特定的数值;

(6)属性约简。删除决策表中对决策属性不重要的或者不必要的条件属性,本文采用的是基于属性重要性的属性约简算法,以下为它的主要步骤。

输入决策表S=(U,C∪D,V,f),其中U={x1,x2,…,xn},C={C1,C2,…,Cn};

输出约简后的属性集Reduct(简称Red);

1)令core(C)=∅;

2)计算相对正域POSC(D),对于任意的一个Ci,若POS(C-{Ci})(D)≠POSC(D),则core(C)=core(C)+{Ci},从而得出属性约简集合Red=core(C);

3)计算γRed(D),γC(D),若γRed(D)=γC(D),转向5),否则转向4);

4)计算剩余属性中属性重要性ECi(D),找出max(ECi(D)),并将其加入Red中,即Red=Red+{Ci},转向3);

5)输出属性约简集Red。

(7)构造SVM分类器。将属性约简后的训练数据作为SVM的输入量,通过训练问句训练集构造最小误差分类器,并以该分类器对问句测试集进行测试;

(8)分类效果评价。将CRV所得到的分类结果与直接进行SVM分类的结果进行比较,若分类效果比较明显则转步骤9,若分类效果不理想,则需要返回步骤3进行重新处理;

(9)分类结果。

3 实验及结果分析

为验证CRV方法的对与问题分类的可行性和有效性,本文通过计算机网络课程的自动问答系统中对学生提出的问题进行分类,从问题库中提取问句集样本,并将其扩展为1 200个问句,包括796个训练问句,404个问句测试,将其分为8类,各类的训练集数目和测试集数目如表1所示。

对问句集样本进行属性约简,将约简后的样本数据作为SVM的输入量,使用LIBSVM 2.89在Matlab6.5上实现问题分类。将该方法与直接进行SVM分类进行比较,实验结果如表2所示,通过属性约简,将数据空间维数由1 200降低到923,其平均分类准确率由85.39%提高到了86.06%。可以看出,本文提出的方法优于直接进行SVM分类方法。

表2 CRV和SVM方法的比较

4 结束语

本文研究的CRV方法利用RST对样本数据进行预处理,提高了SVM的分类效率,与直接进行SVM分类相比,减少了数据的空间维数,提高了分类的准确率。但是在该分类过程中有不少的人工干预,而且若特征项的选择不好,都会影响分类的准确率,因此在今后的研究中,减少不必要的人工干预,考虑从更深层的语义来选取特征项。

[1] 蔡刚山.中文自动问答系统研究[D].武汉:华中科技大学,2007.

[2] 李鑫.问答系统中的问题分类研究[D].上海:复旦大学,2007.

[3] Vapnik V.The Nature of Statistical Theory[M].New York:Sp ringer-Verlag,1995:2-57.

[4] 邓乃杨,甜英杰.支持向量机:理论、算法和拓展[M].北京:科学出版社,2009:1-125.

[5] Pawlak Z.Rough Sets Theoretical Aspects of Reasoning about Data[M].Boston:Kluwer Academ ic Publishers,1991:1-150.

[6] 史军.基于粗糙集理论的属性约简算法研究[D].青岛:青岛大学,2009.