监听时间对声纳浮标阵检查性搜索效能影响仿真

袁 杰，丛红日，李 琰，王光源

（1.海军装备部军械保障部，北京 100841；2.海军航空工程学院指挥系，山东 烟台 264001；3.91917部队，北京 100036）

声纳浮标通常需要组成声纳浮标阵才能有效地进行搜索。影响声纳浮标阵搜索效能的因素非常复杂，其中，监听时间是影响声纳浮标阵搜索效能的关键因素。目前，在作战或训练过程中，还没有科学确定声纳浮标阵监听时间的方法，制约了声纳浮标阵作战效能的发挥。本文试图通过采用蒙特卡洛法进行仿真研究来解决这一问题。

对于声纳浮标阵的搜索来说，搜索概率是其核心效能指标。声纳浮标阵的搜索概率P搜索是指：在搜索区内如果存在潜艇，则通过搜索能够发现目标潜艇的概率[1]。

1 仿真模型建立

1.1 典型条件

由于影响声纳浮标阵搜索效能的因素非常复杂，为了便于进行仿真研究，有必要设定一定的典型条件。

1）作战样式为检查性反潜。

不同作战样式下，由于作战条件不同，即使是完全相同的声纳浮标阵，其搜索效能也存在很大差异。因此，研究声纳浮标阵的搜索效能，必须针对具体的作战样式。

与其他作战样式相比，检查性反潜时偶然因素对作战的影响最小，制约条件也最少。因此，以检查性反潜作为背景来研究声纳浮标阵的搜索效能，就可以尽可能地忽略偶然因素的影响，从而突出主要因素的影响[2]。

2）搜索区为长方形区域。

根据检查性搜索的特点，搜索区一般设为方形、圆形等规则形状。这里设定为最常用、最典型的长方形搜索区，其边长分别为L1和L2。

3）声纳浮标阵阵型为方形阵。

声纳浮标阵阵型对其搜索效能有重要影响[3]。方形声纳浮标阵是一种最简单的包围型浮标阵，在检查性反潜中广泛应用[2]。由于搜索区为长方形区域，因此，这里设定为与之相对应的长方形声纳浮标阵。

长方形声纳浮标阵沿长方形搜索区域的内沿均匀布设。

4）先布设后监听声纳浮标阵。

使用声纳浮标阵搜索包括布设和监听两个方面。主要有两种方式：先布设后监听和边布设边监听[1]。

采用先布设后监听声纳浮标阵的方式，可以把作战过程区分为布设浮标阵和监听浮标阵两个独立的阶段，有利于集中研究监听对声纳浮标阵搜索效能的影响。

5）搜索区内存在目标潜艇。

本假设纯粹是为了研究的方便。

6）目标潜艇的初始位置和航行状态未知，但确定在进行检查性搜索时，目标潜艇的初始位置和航行状态都是未知的。

基于检查性反潜的特点，假设目标潜艇的初始位置和航向均服从均匀分布，且不中途改变航行状态[4]。

1.2 基准时间的确定

以开始对声纳浮标阵进行监听的时刻为基准时间t0，这样，目标潜艇运动的时间和监听声纳浮标阵的时间就可以统一表示。

1.3 坐标系建立及搜索区域、浮标阵位置表示

坐标系建立应综合考虑搜索区域、声纳浮标阵、目标潜艇位置表示的需要，以方便研究问题为原则。

以长方形搜索区的任意一个顶点为坐标原点，以与该点相邻的两条边的方向为坐标轴建立平面直角坐标系。

使用该坐标系，就可以方便地表示检查性搜索区域。而根据设定的条件，声纳浮标阵在搜索区域中的位置也可以方便地表示出来。如图1所示。

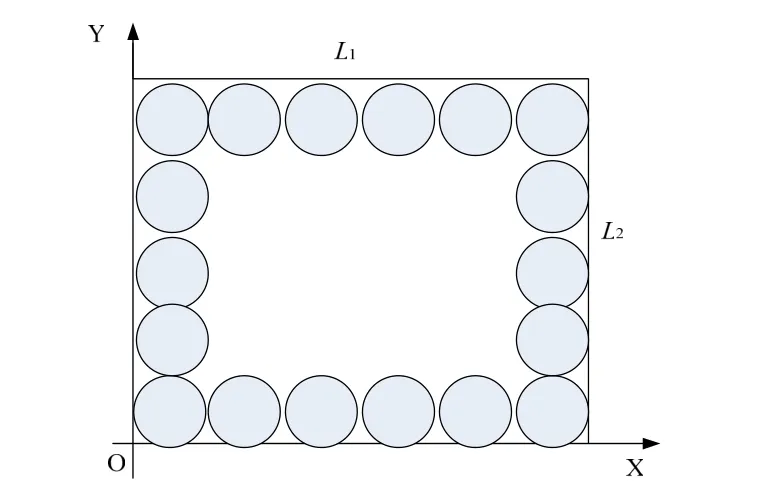
图1 搜索区域及浮标阵位置示意图

1.4 声纳浮标位置表示

理论上讲，搜索区域的位置和大小、声纳浮标阵在搜索区域中所处的位置、声纳浮标有效探测距离D浮声、声纳浮标阵内各声纳浮标之间的间距 d浮声确定后，组成声纳浮标阵的声纳浮标的数量N浮声以及各枚声纳浮标的位置(xn,yn)也就惟一的确定了。

但这样确定的声纳浮标的位置只是理论位置。而在实际作战过程中，由于直升机定位精度、机组训练水平等方面的原因，每枚声纳浮标不可能准确布设于其理论位置，必然会存在一定误差。此外，声纳浮标布设后，由于受到气象水文条件的影响，其位置还会产生漂移，这也会产生位置误差。

设每枚声纳浮标的实际位置为(x实n,y实n)，平均误差为ω，则根据误差理论，声纳浮标位置服从以(xn,yn)为均值、以ω为均方差的正态分布。则对于每枚声纳浮标都可以使用服从该正态分布的随机数来生成位置误差。

设随机数ω1和ω2相互独立，且均服从以0为均值以ω为均方差的正态分布，则：

1.5 目标潜艇位置表示

1）目标潜艇初始位置生成。

目标潜艇初始位置就是在基准时间t0时目标潜艇所处的位置。根据检查性反潜的特点，一般假设目标潜艇的初始位置在检查性搜索区内服从均匀分布[5]。

设ξ1和ξ2为相互独立的2个随机数，ξ1和ξ2均服从均匀分布，且0≤ξ1≤1、0≤ξ2≤1，则目标潜艇初始位置坐标 (x0,y0)可以表示为：

2）目标潜艇航向生成。

检查性搜索时，一般也假设目标潜艇的航向服从均匀分布。由于方向在平面坐标中是一维的，只需要一个随机数即可。设该随机数为ξ3，服从均匀分布，且0≤ξ3≤1，则目标潜艇的航向与x轴之间的夹角θ可以表示为：

3）目标潜艇航速生成。

目标潜艇通常以小噪声航速航行。设目标潜艇的最小小噪声航速为v潜小，目标潜艇的最大小噪声航速为v潜大，则一般认为目标潜艇的实际航速v潜在v潜小和v潜大之间服从均匀分布[6]。

设随机数ξ4服从均匀分布，且0≤ξ4≤1，则v潜可以表示为：

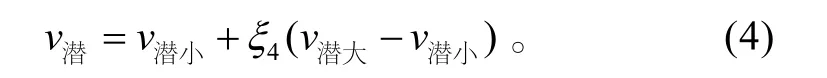
4）目标潜艇运动方程。

基于假设，目标潜艇的运动方程为：

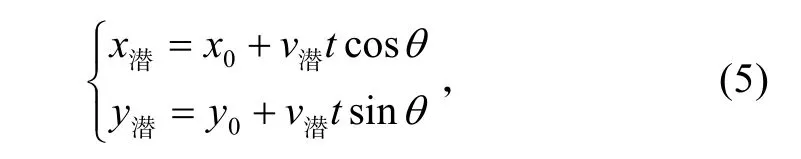
式中，t为从t0时刻开始目标潜艇的航行时间，也是监听声纳浮标阵的时间。

使用上述运动方程，就可以计算出任意时刻目标潜艇位置的坐标(x潜,y潜)。

1.6 声纳浮标阵搜潜机理分析

声纳浮标阵能够搜索到目标潜艇，必须具备3个方面的条件：一是目标潜艇能够进入到声纳浮标阵的有效搜索范围；二是声纳浮标能够可靠工作；三是声纳员能够有效进行监听[7]。显然，这3个方面的条件之间是相互独立的。

设：目标潜艇进入声纳浮标阵有效搜索区域的概率为P进入，声纳浮标的可靠性为P可靠，当目标潜艇已经进入到声纳浮标阵有效搜索区域范围之内且声纳浮标能可靠工作时能够监听到目标潜艇的概率为P监听，则：

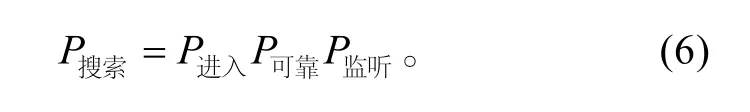
1.7 仿真模型建立方法

上面所建立的只是声纳浮标阵搜索效能的理论模型。但在实际仿真时，采用基于蒙特卡洛方法的仿真模型[8]。

由于以t 对P搜索的影响为研究对象，因此，采用按时间步长推进的仿真方法[9]。以t0为基准时间，采用下面的判别方法对声纳浮标阵能否搜索到目标潜艇进行判别。如果在当前时刻没有搜索到敌潜艇，则按选定的时间步长继续推进到下一个时刻进行判别，直至搜索到目标潜艇或达到规定的最大搜索时间；如果搜索到目标潜艇，则本次仿真过程结束，当前时刻的搜索成功次数加1。

重复进行上述过程直至规定的最大仿真次数。这样，在每一时刻，都累积了一定数量的搜索成功次数，再对所有仿真结果进行统计分析，就可得出到当前时刻为止的搜索概率。

1.8 搜索效果判别

1）目标潜艇能否进入声纳浮标阵有效搜索范围。

目标潜艇进入声纳浮标阵的有效搜索范围，也就是进入组成声纳浮标阵的至少一枚声纳浮标的有效搜索范围。

当声纳浮标阵布设完成后，如果不考虑声纳浮标的漂移，则在监听过程中，可以认为每枚声纳浮标的位置 (x 实n,y实n)是固定的。但目标潜艇一般处于持续的运动过程中，其位置(x潜,y潜)时刻发生改变。

每枚声纳浮标的有效搜索范围都是以(x 实n,y实n)为圆心以D浮声为半径的圆形区域。因此，在任意时刻，只要依次计算目标潜艇当前位置点与每枚声纳浮标之间的距离dn：

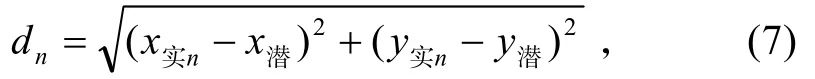
2）声纳浮标能否可靠工作。

P可靠包括布设时的成活率和布设成活后的可靠性两个方面。如果布设时没有成活一般会补充布设，所以一般只需考虑第二个方面的因素。

P可靠主要取决于装备性能、战场环境，与使用时间也有关系。但由于与本文的研究关系不密切，这里不展开讨论，而是合理地给出一个固定值。

仿真时使用随机数来进行判别。设随机数ξ5服从均匀分布，且0≤ξ5≤1，则：当ξ5＜P可靠时，认为声纳浮标可靠工作；而当ξ5≥ P可靠时，认为声纳浮标不能可靠工作。

3）能否成功监听。

P监听表示的是监听能力，主要取决于装备性能和声纳员的训练水平，这里也不展开讨论，只是合理给出一个固定值。

仿真时也使用随机数来进行判别。设随机数ξ6服从均匀分布，且0≤ξ6≤1，则：当ξ6＜P监听时，认为能监听到目标潜艇；而 ξ6≥ P监听时，认为不能监听到目标潜艇。

2 仿真研究

2.1 仿真想定

1）检查性搜索区为一长方形区域，L1=××km，L2=××km。

2）使用非定向被动式声纳浮标，型号为××，D浮声=××km。

3）d浮声=2 D浮声。

4）ω=100 m。

5）目标潜艇为常规动力潜艇，型号为××，v潜小=××kn，v潜大=××kn。

6）P可靠=0.95，P监听=0.9。

7）最大搜索时间T=4 h。

2.2 仿真程序

仿真程序框图如图2所示。

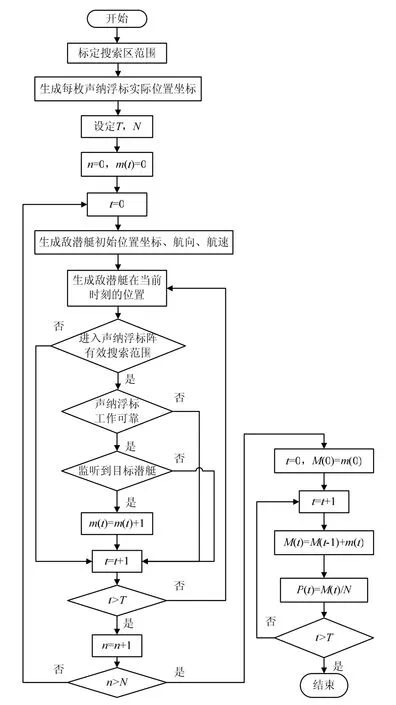
图2 仿真程序框图

图2中，t、T分别表示当前监听时刻和最大监听时间；n、N分别表示当前仿真次数和最大仿真次数；m(t)、M (t)分别表示某一时刻探测到目标潜艇的次数和到当前时刻为止累计探测到目标潜艇的总次数；P (t)表示当前时刻的搜索概率。

仿真程序使用C++语言编程实现。

2.3 仿真步长与仿真次数

仿真步长和仿真次数对仿真结果的精度有重要影响。综合考虑声纳浮标阵搜索的特点和仿真结果的需要，仿真步长设定为1 min，仿真次数均设定为10 000次。

2.4 仿真结果

仿真结果如图3所示。

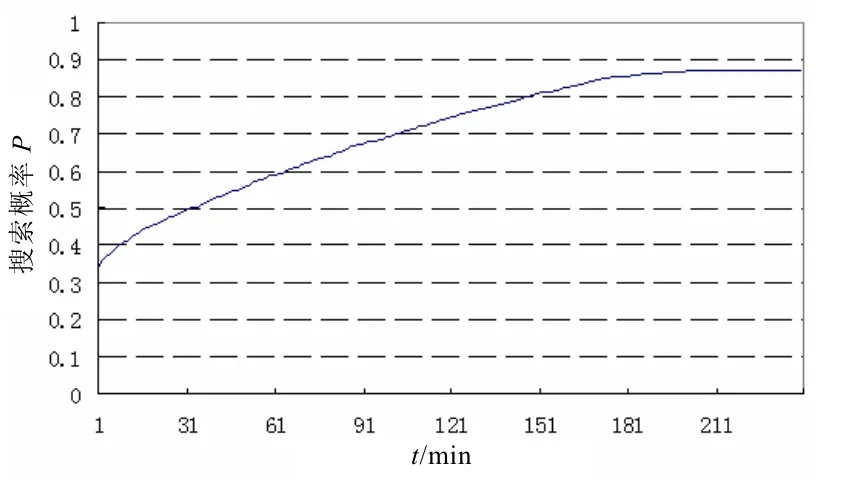
图3 仿真结果图

2.5 仿真结果分析

从仿真结果可以看出：

1）声纳浮标阵的搜索效能随监听时间的增加而提高，与战术常识及部队的实际训练结果相吻合。

2）只要开始监听，就可以取得比较高的搜索概率，在本例中大约为0.35。当然，在实际监听过程中，真正监听到目标潜艇仍然需要花费一定时间，但这个时间通常比较短。

事实上，这个初始搜索概率是声纳浮标阵有效搜索范围占整个搜索区面积比值的体现，是前一个作战阶段即布设声纳浮标阵阶段工作在搜索效能上的反映。

其战术意义在于：首先，应尽量提高声纳浮标的有效探测距离，并尽量多布设浮标，以尽可能地提高初始搜索概率；其次，初始监听阶段非常关键，需要声纳员监听时注意力高度集中。

3）监听时间的增加和搜索效能的提高不是简单的线性关系。从总体上看，随着监听时间的增加，搜索效能提高的幅度逐渐降低，但表现得并不均匀。大致可划分为以下3个阶段：

① 快速提高期。

大致为从开始监听到监听30 min时。在最初的这段时间内，随着监听时间的增加，搜索效能提高较快。至30 min时，搜索概率大约为0.5，比开始监听时大约提高0.15。

其战术意义在于：当没有条件长时间进行监听时，也能够取得相对比较理想的搜索概率。

② 平稳提高期。

大致的时间段为30～180 min。在这段时间内，搜索效能提高的幅度虽然有所降低，但仍然稳步提高。总体表现为随着监听时间的增加，搜索效能以近似于线性的方式提高。至180 min时，搜索概率提高至约0.86。

其战术意义在于：如果有条件较长时间地进行监听，就应适当延长监听时间，以取得更为理想的搜索效果。

③ 滞涨期。

大约从180 min 开始，随着监听时间的增加，搜索效能提高的幅度很小，可以忽略不计。

其战术意义在于：如超过了一定监听时间（本例中大约为180 min），则很难依靠增加监听时间的方法来进一步提高搜索效能。此时，声纳员已经非常疲劳，声纳浮标的可靠性也会下降，甚至会超过声纳浮标的有效工作时间，这进一步降低了搜索效能提高的可能性。如果需要进一步提高搜索效能，则需要采取增加浮标数量、改变阵型等其他方法。

3 结束语

本文以方形声纳浮标阵检查性反潜为背景，通过分析声纳浮标阵的作战机理，建立了其搜索效能的仿真模型，研究了监听时间对声纳浮标阵搜索效能的影响，给出了仿真结果并对其进行了分析。

仿真结果表明：声纳浮标阵的搜索效能随着监听时间的增加而提高，但呈现出比较明显的非线性特征。因此，应根据作战条件和作战要求合理确定监听时间，以提高兵力的使用效率，取得理想的搜索效果。

[1]孙明太.航空反潜战术[M].北京∶军事科学出版社,2003∶86-99.

[2]丛红日.航空反潜战术[M].烟台∶海军航空工程学院,2008∶32-52.

[3]杨日杰,王正红,周旭,等.浮标阵型对搜索效能影响的研究[J].计算机仿真,2009,26(12)∶16-20.

[4]屈也频,廖瑛.潜艇位置散布规律与搜潜效能评估模型研究[J].系统仿真学报,2008,20(12)∶3280-3283.

[5]董文洪,杨日杰,田宝国.航空搜潜声纳浮标位置计算方法研究[J].测试技术学报,2005,19(3)∶383-387.

[6]徐俊艳,何友,杨日杰.被动浮标阵搜潜中积累搜索概率研究[J].测试技术学报,2009,23(1)∶19-22.

[7]丛红日.声纳浮标阵搜潜效能通用仿真模型研究[J].系统仿真技术,2010,6(2)∶104-109.

[8]王磊,吴福初,陈钰宁,等.基于声纳浮标的反潜直升机应召搜潜仿真研究[J].指挥控制与仿真,2010,32(2)∶84-88.

[9]王晓辉,陈建勇,赵红军.直升机吊放声纳搜索方法效能研究[J].火力与指挥控制,2009,34(9)∶18-20.